Contexto
Las vigas de concreto reforzado pueden funcionar normalmente incluso estando fisuradas, es más, casi siempre funcionan así.
En este sentido, tanto para el cálculo de deformaciones (deflexiones) como para el cálculo de la resistencia de la viga, se asume que la viga está fisurada.
En el cálculo de deflexiones de la viga, las fórmulas de deflexión llevan dentro un parámetro de inercia que debe ser calculado para la sección fisurada. Ese parámetro de inercia fisurada es el que analizaremos en este artículo.
Cuadro Resumen
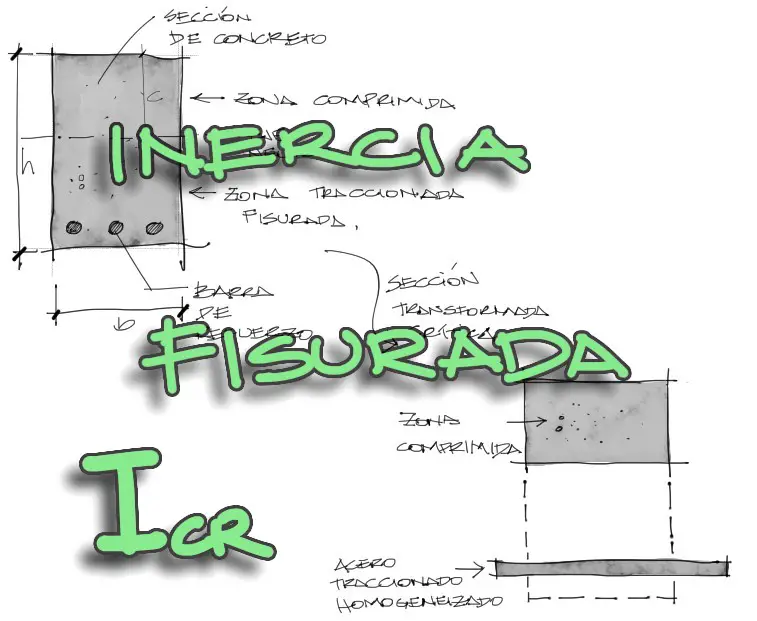
Concepto
La inercia fisurada es la inercia de la sección transversal de concreto fisurada y con las secciones transversales de acero homogeneizadas
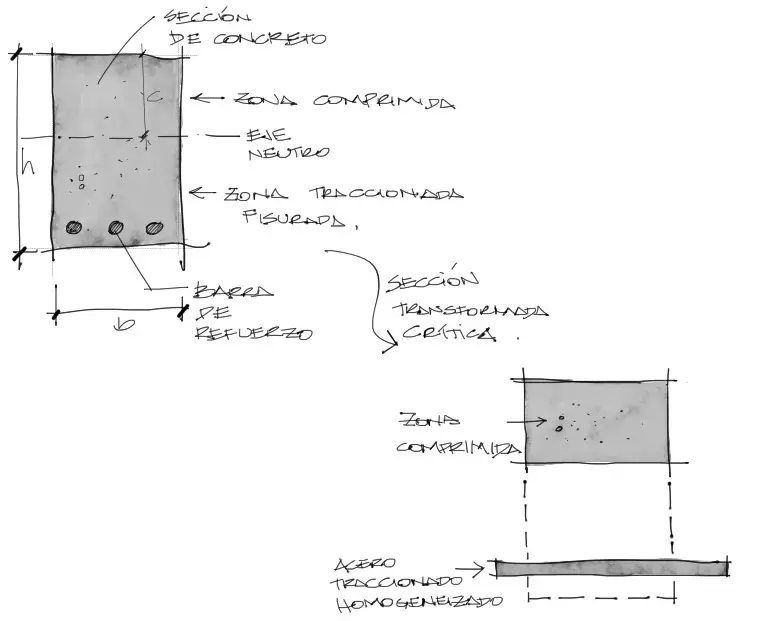
En la imagen se ve que una zona inferior traccionada. Cuando la tracción es considerable, esta zona se fisura, y no aporta a la resistencia a flexión de la viga, y el acero reemplaza a la sección traccionada del concreto fisurado, para resistir la tracción.
Para que sirve
Esta inercia fisurada tiene mucha utilidad al momento de conocer las deflexiones reales de una viga cuando las cargas aplicadas fisuran las zonas de tracción de esta viga.
Cuando una viga está sometida a carga, se dan dos alternativas claras.
1ra Alternativa: La viga no se fisura gracias a que la flexión es pequeña producto de las cargas bajas que no logran fracturar al hormigón y este permanece sin fisuras.
2da Alternativa: Las cargas son significativamente grandes, y fisurarán las caras de tracción de la viga.
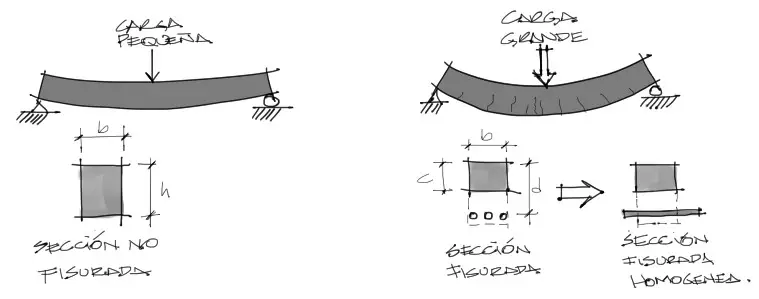
Ya que la deformación de una viga es inversamente proporcional a su inercia, necesitamos conocer la inercia de la sección transversal de la viga para calcular su deflexión.
En la primera alternativa de análisis, el cálculo de las deflexiones es sencillo gracias a que la inercia de la sección transversal de la viga se calcula en base a la inercia de un rectángulo.
En la segunda alternativa, la viga fisurada cambia la forma de su sección transveral. Entonces las deflexiones de la viga ya no pueden calcularse a partir de una sección rectangular de base “b” y altura “h”. La zona de tracción ya no aporta resistencia a la deformación y esta resistencia se transfiere a los aceros. Estos aceros deberán homogeneizarse a las veces de sección de concreto para así calcular la inercia equivalente de la sección transversal fisurada de la viga.
Este proceso de homogeneizar la sección transversal de dos materiales compuestos a un solo material es un artificio utilizado en resistencia de materiales para el cálculo más sencillo de inercias de secciones transversales.
Procedimiento
Datos de entrada
Para resolver la altura del eje neutro de la viga y su inercia fisurada se necesitan los siguientes datos:
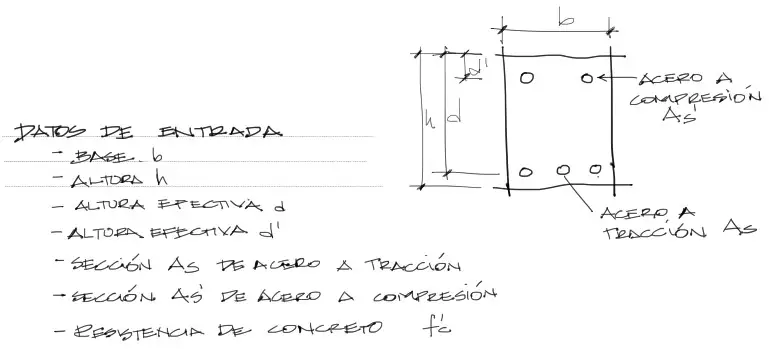
En muchos casos, el acero a compresión As’ será cero. Por otro lado para obtener la elasticidad del concreto se necesita conocer la resitencia del concreto en [MPa]. (generalmente esta resistencia está en el orden de 20 a 30 MPa).
Cálculo de la altura del eje neutro
Antes de calcular la inercia fisurada de la sección necesitamos conocer la altura del eje neutro “c”. Esto se logra equilibrando las areas tanto de la zona de compresión contra las áreas de la zona a tracción.
Debemos notar en la figura siguiente, que las áreas en rojo son las correspondientes a la sección de acero transformada en sección de concreto (sección homogenea). Esto se consigue multiplicando la sección de acero por “n” para el acero a tracción y por “n-1” para el acero a compresión. “n” es el factor de transformación. El motivo por el que el factor de transformación es “n-1” para el acero a compresión es que ésta sección de acero está embebida dentro del concreto a compresión (que también se toma en cuenta en los cálculos), y al transformar el acero a concreto, debemos restarle una vez la sección que ocupan los aceros dentro del concreto.
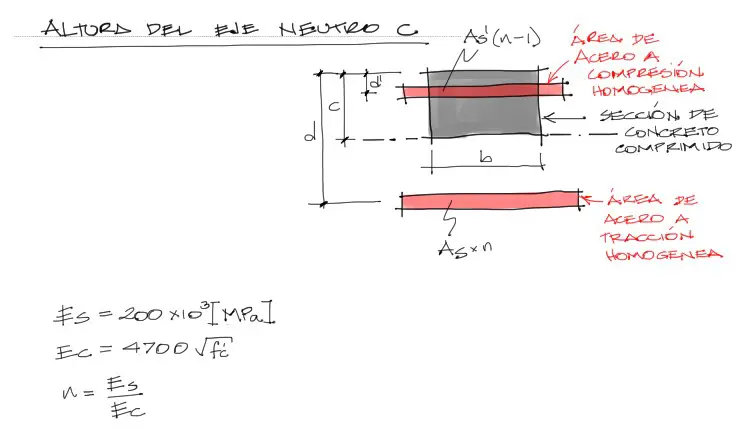
El factor de transformación “n”, recordando conceptos de resistencia de materiales, se calcula como la razón entre el Módulo elástico del acero (que es constante e igual a 200GPa) y el módulo elástico del concreto, que está en función a la resistencia del concreto. En la fórmula de Ec, se debe utilizar la resistencia del concreto fc’ en MPa.
Con todas las áreas y los brazos respecto a su centroide establecidos respecto al eje neutro de la sección, ahora podemos equilibrar las secciones transversales a compresión contra la sección transversal a tracción del acero. La incógnita es la altura del eje neutro “c”.
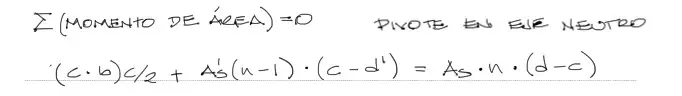
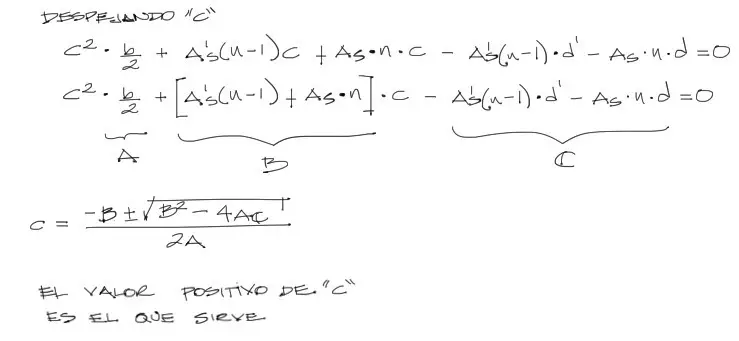
Esto genera una ecuación de segundo grado, que se puede resolver por la fórmula de la ecuación cuadrática, donde la solución que buscamos es la positiva:
Cálculo de la inercia fisurada
Con la altura “c” del eje neutro calculada, encontrar la inercia fisurada Icr. El término “cr” representa “cracked” en inglés, y no “crítica” como se suele pensar.
Para calcular la inercia Icr de la sección fisurada, se deben sumar las inercias de todas las secciones transversales (dos de acero y una de concreto). Además debemos recordar el teorema de ejes paralelos, donde Ixx = Ixx_centroide + A*brazo^2. Tomemos en cuenta que la inercia respecto del centroide de las barras de acero es tan pequeña, que solo debemos tomar en cuenta la fracción A*brazo^2 de estas secciones transversales.

Y con esto se terminan los cálculos
Qué sigue?
Con esta inercia fisurada ya se puede proceder con el cálculo de las deformaciones en servicio de la viga en cuestión, en función a las directrices de la norma ACI que se explicarán en el siguiente artículo: Deflexiones inmediatas en vigas de concreto reforzado.
autor: Marcelo Pardo



Profesor muy buenas madrugadas, disculpe por importunarlo nuevamente, le comento una inquietud. En mis clases de concreto he realizado los procedimientos y al final con el teorema de ejes paralelos tuve un debate sobre que momento de inercia utilizar, ya que el libro del profesor para una viga típica de concreto rectangular utiliza (b*h^3)/3 y no (b*h^3)/12, este cambio con el denominador creo que el cambio al denominador 3 en lugar del 12 va en función de si es una viga en T ó si es una viga rectangular (por el tema de los ejes en el área de concreto). En cualquier caso le agradecería muchísimo sus comentarios. Saludos , usted es el mejor profe!!
Hola buen día, tuve la misma duda, y creo que es porque el denominador /3 indica que la inercia está calculada con respecto a su base y no /12 ya que esta es la inercia que se calcula con respecto al eje centroidal y para este caso no aplica.
Claro que esta el denominador /3, al sumar los términos para el calculo del I_concreto
Muy Didáctico e Interesante
Muchas gracias José Luis!
Excelente Marcelo, muy clara la explicación, muchas gracias por tu dedicación
Muchisimas gracias German