Planteamiento
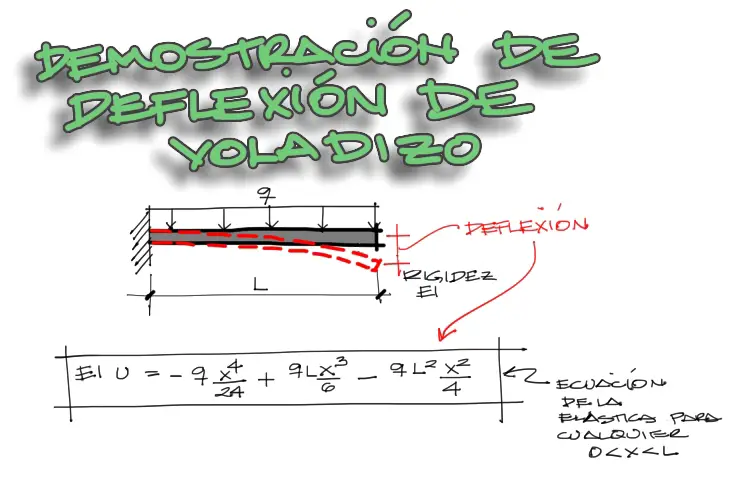
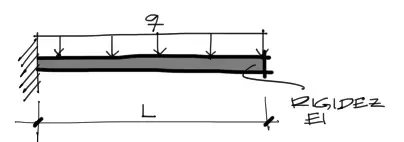
Se quiere determinar la deflexión en el extremo derecho de la viga en voladizo mostrada en la imagen. La longitud de la viga es “L” y su rigidez “EI”. Además está sometida a una carga distribuida “q” constante.
Ecuación de la elástica
Se procederá con la resolución por la ecuación de la elástica por ser la más completa. Este proceso nos entrega la ecuación de la deflexión de la viga para cualquier punto de la misma, y no solo para el extremo derecho. Lo mismo sucede con su pendiente.
La ecuación de la elástica es la siguiente:

En su forma genérica, la carga puede variar en función de “x” pero en nuestro caso la carga es constante.
Integración 4 veces
Para resolver la ecuación diferencial de la elástica debemos integrarla 4 veces. Para cuatro integraciones aparecen 4 constantes de integración que aparecen en la imagen abajo.
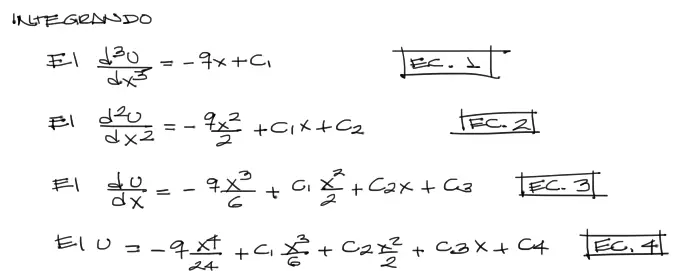
Condiciones de contorno
Para conocer el valor de las 4 condiciones de contorno generadas, debemos conocer las condiciones de contorno del problema. En este caso en particular la viga no se deflecta ni gira en el extremo izquierdo, por tanto en X=0, la deflexión de la viga es u=0 y su pendiente también du/dx = 0.
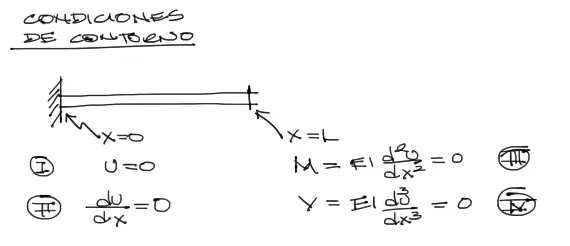
Por otro lado, en el extremo derecho la pendiente y deflexión son máximas y desconocidas. Lo que sí es conocido en el extremo derecho de la viga es su momento flector (que es equivalente a EId2u/dx2) y el cortante (que es lo mismo que EId3u/dx3) que en ambos casos son cero (por estática).
Reemplazo de condiciones
Se reemplazan las 4 condiciones de contorno en las ecuaciones integradas anteriormente. Comenzamos con la condición de desplazamiento u=0 en x=0 en la ecuación integrada Ec.4. hacemos lo mismo con la condición de pendiente en x=0 du/dx = 0 en la Ec.3
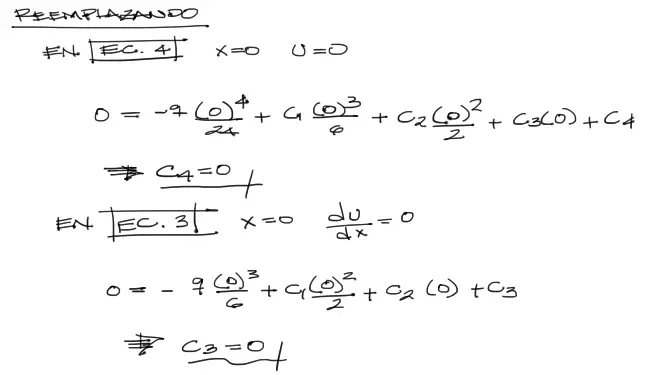
Para las condiciones de contorno en X=L se realiza el mismo proceso pero obviamente reemplazando las condiciones en Ec.2 y Ec.1 respectivamente. Sin embargo a diferencia de los anteriores dos reemplazos donde C3 y C4 se hacen cero inmediatamente, en el caso de las últimas dos se genera un sistema de dos ecuaciones con dos incógnitas C1 y C2.
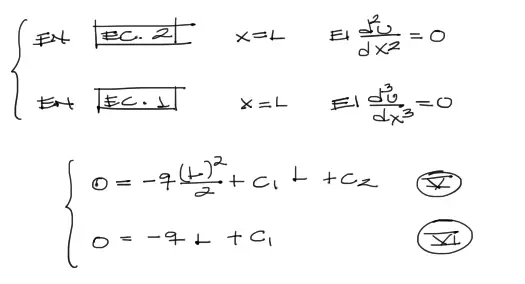
Resolviendo el sistema:

Ecuación de la deflexión
Se reemplazan las 4 constantes C1 a C4 dentro de la ecuación de la elástica integrada 4 veces y se obtiene:

Ésta es la ecuación de la deflexión para cualquier punto de la viga “x”. Si queremos la deflexión en el extremo derecho de la viga simplemente reemplazamos x=L y operamos.

Ecuación de la pendiente de deflexión
Para conocer la pendiente de la deflexión en cualquier punto de la viga debemos reemplazar las 4 constantes C1 a C4 en la tercera ecuación integrada de la elástica (pues en esta ecuación aparece la pendiente du/dx de la viga).
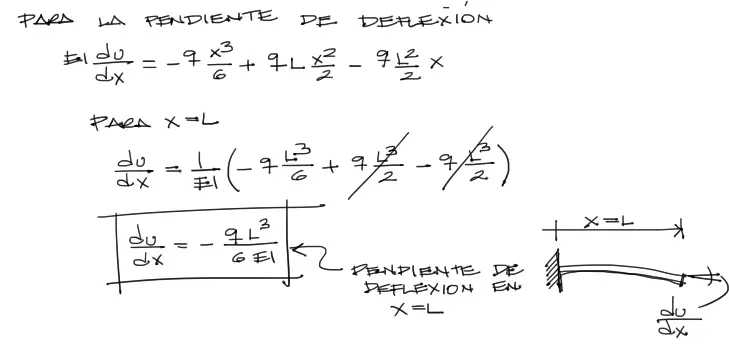
Con esto ya se tiene toda la información de la deformada de la viga.
autor: Marcelo Pardo
←←← VOLVER A TABLA DE CONTENIDO DE RESISTENCIA DE MATERIALES ←←←


