
Enunciado
Encontrar a partir de las fórmulas de integración de la inercia, las inercias Ixx, Iyy respecto a los ejes cartesianos del triángulo mostrado a continuación. Posteriormente encontrar la inercia del mismo triángulo respecto a su centroide.
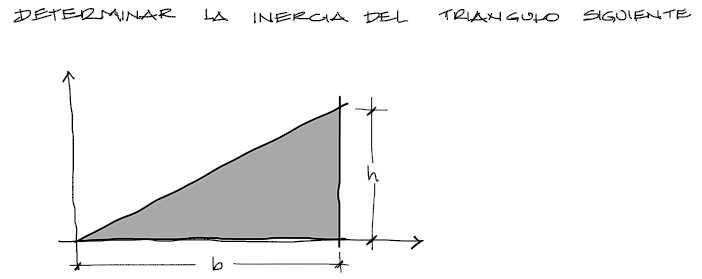
Resolución de Inercias Ixx y Iyy
El primer paso para encontrar las inercias a partir de las fórmulas de integración es conocer las funciones Y(x) de cada una de las curvas (o rectas) que delimitan el triángulo hacia arriba y hacia abajo. Para esto utilizamos la fórmula genérica de la ecuación de la recta:
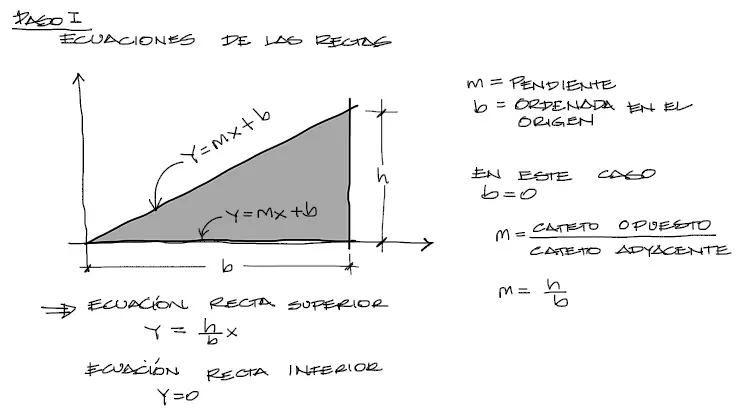
Estas fórmulas a continuación se vuelven los límites superior e inferior en la integración de la inercia. Las fórmulas de inercia para superficies Ixx y Iyy son las siguientes:

En estas integrales, lo más conveniente es descomponer la diferencial de área dA en dy·dx y luego reemplazar los límites. En el reemplazo de límites en X no necesitamos escribir la fórmula de las rectas de X en función de Y sino simplemente los valores de los extremos de la figura. Entonces se tiene:

Repetimos el procedimiento respecto al eje Y:
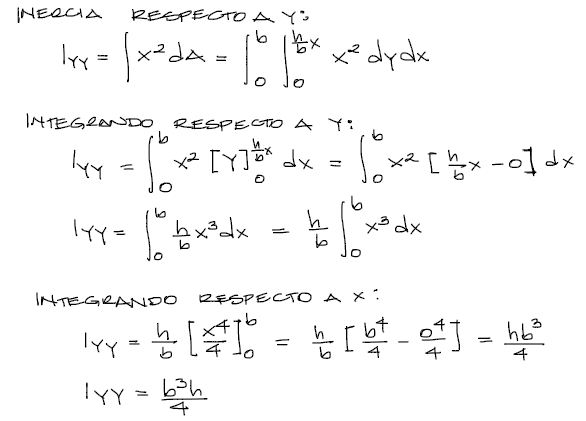
Con esto ya hemos conseguido las inercias respecto al extremo inferior izquierdo del triángulo
Inercias respecto del centroide de la figura
Para encontrar la inercia del triángulo respecto de su centroide tenemos dos caminos. El primero consiste entrasladar “manualmente” el triángulo haciendo coincidir el eje centroidal de la figura con los ejes coordenados, y luego repetir el procedimiento descrito arriba tomando en cuenta que incluso las funciones de límites superior e inferior cambiarían, por lo que habría que recalcularlas antes de calcular las integrales.
El segundo camino más sencillo es el de utilizar la fórmula del teorema de ejes paralelos. Este teorema indica que podemos conocer la inercia de una figura respecto de cualquier punto si conocemos la inercia respecto del centroide, el brazo de traslación y el área de la figura.
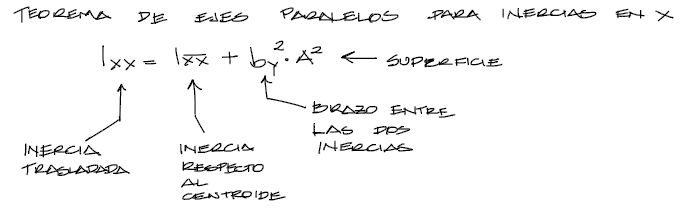
En nuestro caso no conocemos la inercia respecto del centroide, pero conocemos la inercia trasladada. Por tanto para las inercias Ixx hacemos el reemplazo de los valores conocidos, y despejamos la inercia respecto del centroide:
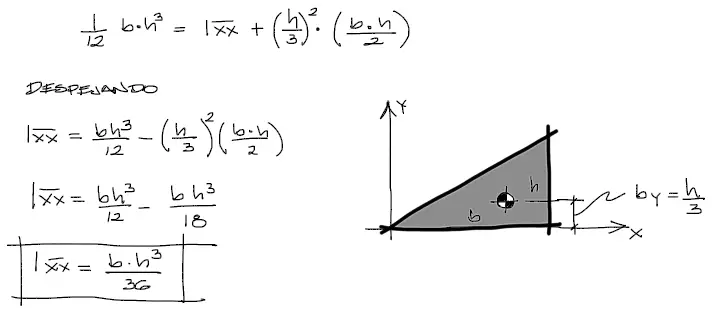
Haciendo el despeje, en pocos pasos hemos obtenido la inercia respecto del centroide. Debemos tomar en cuenta que el brazo a calcular es la distancia desde la inercia trasladada hasta la inercia respecto del centroide medida perpendicularmente al eje con el que se trabaje.
Repetimos el procedimiento para la inercia centroidal Iyy:
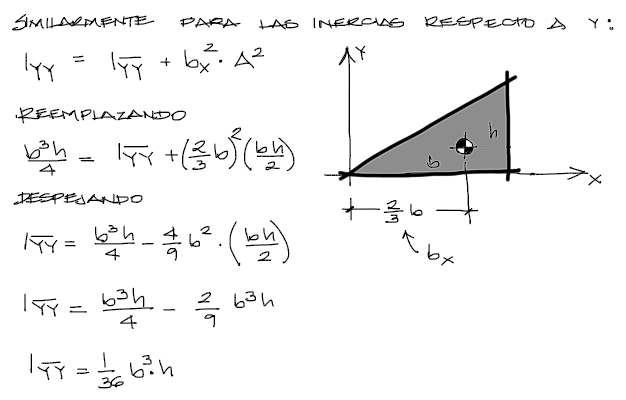
Resumen de inercias encontradas
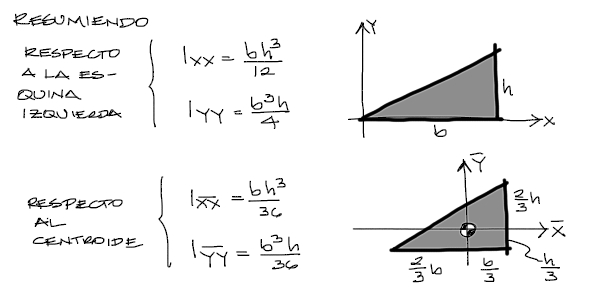
Con esto termina el ejercicio.
autor: Marcelo Pardo
←←← VOLVER A TABLA DE CONTENIDO DE RESISTENCIA DE MATERIALES ←←←


