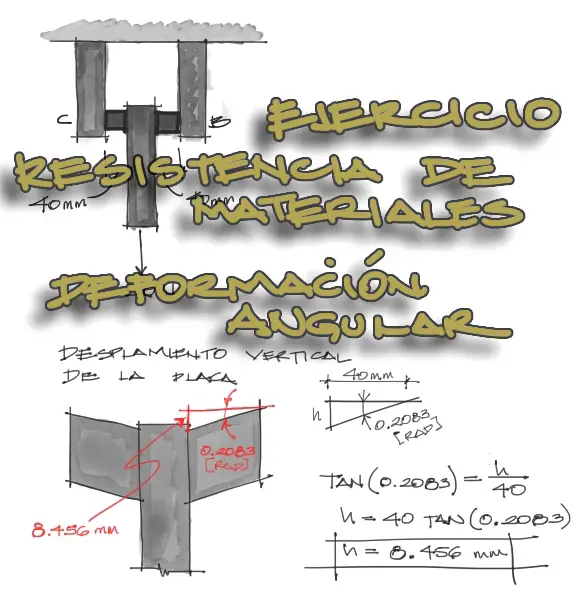
Enunciado

El soporte consta de tres placas rígidas conectadas entre sí por medio de dos cojinetes de hule situados simétricamente. Si se aplica una fuerza vertical de 50 N a la placa A, determine el desplazamiento vertical aproximado de esta placa debido a las deformaciones unitarias cortanes en el hule. Cada cojinete tiene dimensiones de 30 mm y 20 mm. G = 0.20 [MPa].

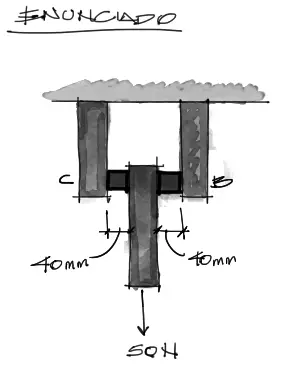
Equilibrio externo

Por simetría podemos deducir que mitad de los 15N se van a cada brazo empotrado en el cielo. Entonces matemáticamente se tiene:

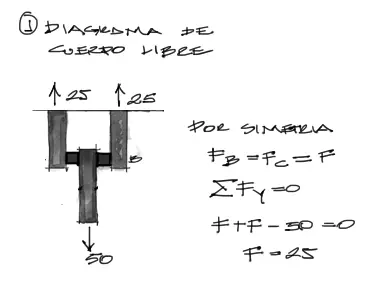
Esfuerzos de cortante

Como en todo problema, las fuerzas de contacto entre los tacos de hule con las piezas metálicas son de cortante. Estas fuerzas se pueden visualizar en el esquema siguiente:

Las fuerzas tangentes de 25N se convierten en esfuerzos al dividir la fuerza entre el área de contacto:

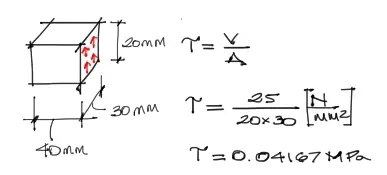
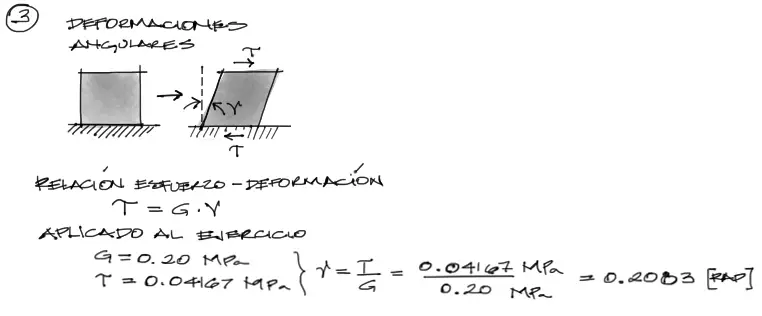
Deformación angular

Existe una relación directa entre un esfuerzo tangencial y la respectiva deformada angular de una pieza a través del módulo de corte G. Si a partir de esta relación despejamos la deformación angular, se obtiene una deformación angular de 0.2083[rad]

Desplazamiento vertical

A partir de aquí solo resta aplicar un poco de trigonometría para darnos cuenta que para una deformación angular de 0.2083[rad], la pieza de neopreno desplaza una de sus caras una distancia h igual a:

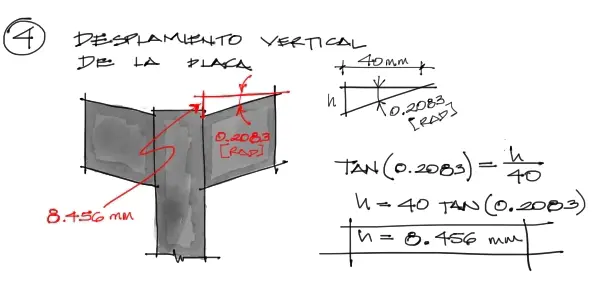
Con esto termina el ejemplo. La pieza central desciende una distancia de 8.456 [mm] desde su posición inicial producto del peso de 50[N].

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE RESISTENCIA DE MATERIALES ←←←