Enunciado
El libro de Cimentaciones – Braja Das plantea en su ejercicio 6.3, el siguiente problema:
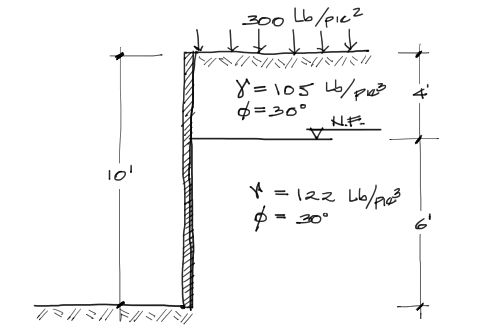
Se desea encontrar la fuerza de empuje en reposo y el punto de aplicación de la resultante para el corte mostrado.
A los 6 pies se encuentra nivel freático y por tanto el suelo por debajo de esa cota está sumergido. El peso especifico de 122 Lb/pie3 es saturado. Además se tiene una sobrecarga de 300 Lb/pie2 aplicado en la corona.
Resolución
Esfuerzos de empuje
El enunciado menciona “En reposo” por lo que se refiere al empuje del suelo cuando el muro no se desplaza absolutamente ninguna distancia hacia la izquierda. Este es el caso típico de muros de contención de edificios donde se vacía el muro inmediatamente después de realizar el corte.
El coeficiente de empuje en reposo para arenas es:
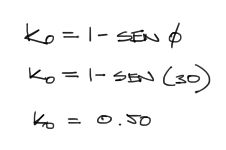
Con este coeficiente encontramos los esfuerzos horizontales de empuje. Estos esfuerzos son triangulares para el suelo y se incrementan con la profundidad como en la siguiente imagen. En contraparte, el empuje por sobrecarga por encima de la corona es rectangular.
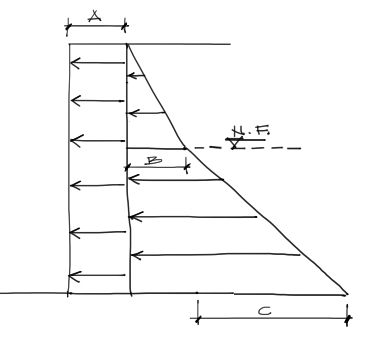
Las etiquetas A, B, C denotan el esfuerzo de empuje horizontal en cada punto, y se encontrarán a continuación.
- A = Esfuerzo de empuje por sobrecarga
- B = Esfuerzo de empuje por el suelo seco encima del N.F.
- C = Esfuerzo del suelo sumergido por debajo del N.F.
Se observa un quiebre en la pendiente de esfuerzos justo a la altura de 6′. Esto se debe a que por debajo del nivel freático el empuje está compuesto de la suma del EFECTIVO efectivo del suelo más el empuje del agua. Se verá a detalle este fenómeno más abajo.
Esfuerzo por sobrecarga
Para calcular el esfuerzo rectangular tomamos como parámetros la sobrecarga qo, el factor de empuje en reposo ko. Luego el esfuerzo horizontal es qo*ko:

Esfuerzo horizontal por suelo seco
El esfuerzo horizontal de empuje de cualquier suelo no sumergido está dado por la fórmula σ = ɤs*ko*h donde:
- ko: factor de empuje en reposo
- ɤs: Peso específico del suelo
- h: altura de la masa de suelo
Aplicando las espectivas magnitudes se tiene:

Esfuerzo horizontal debido al suelo sumergido + empuje del agua
Los datos para esta franja de suelo de 6 pies son los siguientes:

El peso específico del suelo SATURADO es de 122 Lb/pie3. Adicionalmente sabemos que el peso específico del agua en unidades inglesas es de 62.4 Lb/pie3 (dato obtenido de fuentes externas).
Es sabido en mecánica de suelos, que cuando un suelo está sumergido, su empuje pasivo está compuesto por el peso específico efectivo del suelo (ɤs-ɤH2O) multiplicado por el factor Ko y la altura de la franja de suelo.

Por otro lado debemos sumarle a este empuje, el empuje debido al agua, que como es bien sabido de física, tiene un empuje de ɤH2O*h. En este caso obtenemos entonces:

Finalmente debemos sumar ambos esfuerzos, el efectivo del suelo más el esfuerzo del agua:

Resultante de esfuerzos
Las fuerzas resultantes de cada bloque de esfuerzos obtenidos arriba, se obtiene calculando el “área” de cada bloque de esfuerzos (donde el resultado obtenido obviamente no estará en unidades de superficie, sino en unidades de fuerza).
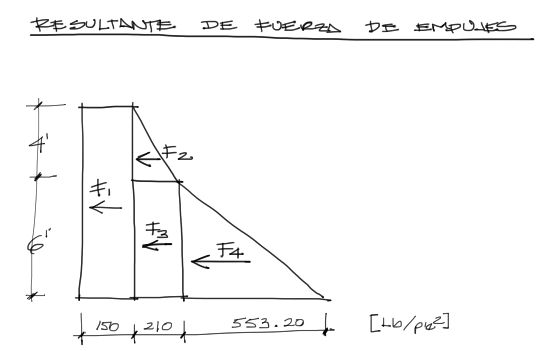
Se separa en este caso todo el conjunto de esfuerzos en bloques rectangulares y triangulares para el cálculo más sencillo de las fuerzas resultantes. Además, se acotan abajo todos los esfuerzos obtenidos hasta el momento para cada uno de los bloques. Calculando entonces las respectivas “áreas”:

Ubicación de la fuerza resultante
El conocer la ubicación (en altura) la suma de las fuerzas resultantes es equivalente a encontrar el centroide de todo el bloque de esfuerzos dibujado arriba, pero en este caso solo nos interesa el centroide en Y o en el sentido vertical.
Para eso debemos aplicar la fórmula de: (Suma de fuerzas X brazo) / (Suma de Fuerzas). En este caso los brazos son la distancia vertical desde la base del corte hasta el punto de aplicación de cada fuerza.
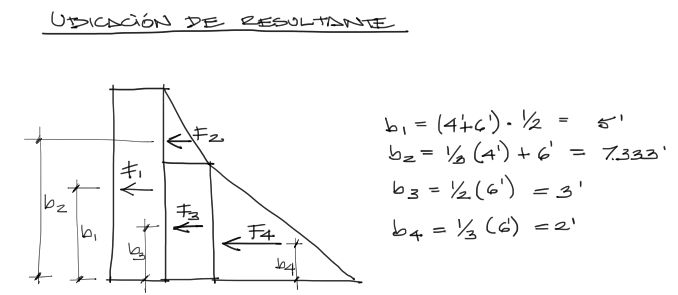
Para los brazos de los bloques rectangulares, el brazo es la mitad de la altura. Para el esfuerzo triangular, el brazo está a 1/3 de la altura del bloque triangular.
Aplicando entonces la fórmula Y = (Suma de fuerzas X brazo) / (Suma de Fuerzas):
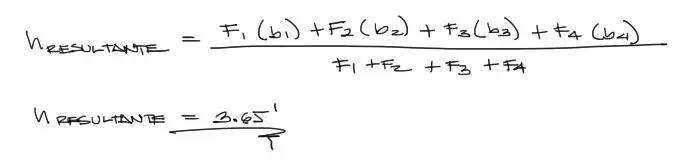
Resumiendo lo que nos pide el enunciado, esquematizamos:
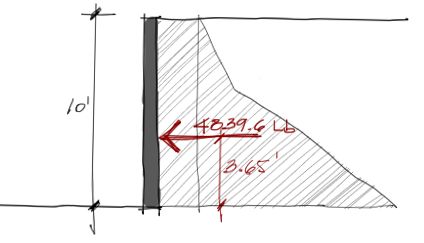
Con esto termina finalmente el ejercicio.
Contexto
El procedimiento de este ejercicio forma parte del cálculo de empuje de suelo hacia muros de contención. En contraparte se suele además calcular el empuje pasivo de izquierda a derecha otorgado por el suelo de la izquierda, dependiendo de la profundidad del muro.
En este esquema de enunciado se dibujó una especie de tablaestaca de 10′ de altura, pero el muro nunca se construye así. El todos los casos el muro entra una profundidad de al rededor de 1/3 de la altura por debajo del pie del corte. En ese sentido, este ejercicio es solo para comprender como se arma un perfil de esfuerzos de empuje de suelo.
autor: Marcelo Pardo