Enunciado

Se pide resolver el ejercicio mostrado

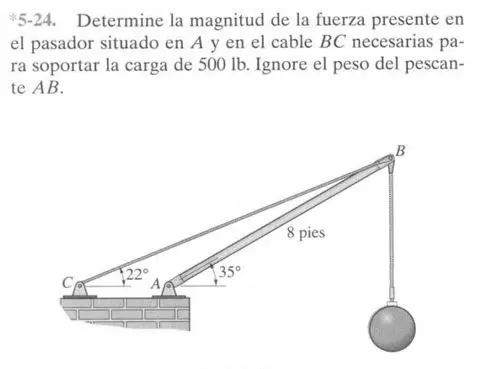
Resolución

El ejercicio puede resolverse de dos maneras distintas. La primera propuesta de resolución consiste en el equilibro externo de la estructura. El segundo método consiste en el equilibrio interno de uno de los “nudos” del sistema. Se verán ambos a continuación.

Método 1 – Equilibrio externo

Cuando se equilibra externamente cualquier estructura, se deben dibujar las reacciones del sistema vectorialmente para luego encontrar sus magnitudes.

Antes de resolver cualquier sistema, debemos encontrar algunas medidas. Primero encontramos las dimensiones de los catetos del triángulo interno conformado por la barra de 8 pies y ángulo de 35°. Encontradas estas distancias, podemos encontrar los datos del triángulo conformado por la barra BC y el ángulo de 22°:

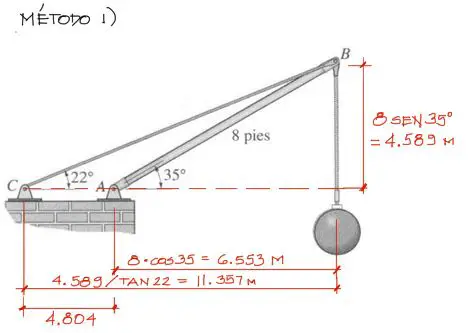
El siguiente paso consiste en dibujar las reacciones del sistema. Las fuerzas Fab y Fcb de color azul pueden descomponerse en función a los ángulos de 35° y 22° respectivamente, como se muestra en la figura:

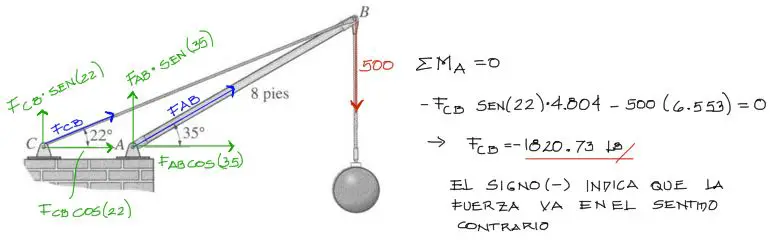
Descompuestas las fuerzas, podemos hacer el equilibrio de las reacciones mediante las tres fórmulas conocidas: Sumatoria de fuerzas en X, sumatoria de fuerzas en Y y sumatoria de Momentos.

En este caso realizaremos la sumatoria de momentos respecto a un punto al cual converjan la mayor cantidad de fuerzas, así estas fuerzas no generan brazo y por tanto no generan momento de fuerza. Ese punto será el punto A. En el gráfico arriba se puede ver la sumatoria de momentos respecto a este punto.

Como en esta ecuación solo queda Fcb como incógnita, esta se despeja y resulta Fcb = -1820.73 Lb

A continuación se puede realizar la suma de fuerzas en X, para así conocer Fab:

Con esto termina el ejercicio. Si se quisiera realizar la sumatoria de fuerzas en Y, esta operación sería redundante y para propósitos de comprobación simplemente, ya que ya se conocen todas las incógnitas del problema.

Método 2 – Equilibrio interno

Se puede aislar un nudo, donde intersectan todas las fuerzas. En este caso aislamos el nudo B y realizamos un diagrama de cuerpo libre. En este diagrama de cuerpo libre existen dos incógnitas Fba y Fbc, y además dos ecuaciones para resolver estas dos incógnitas. Suma de fuerzas en X y suma de fuerzas en Y.

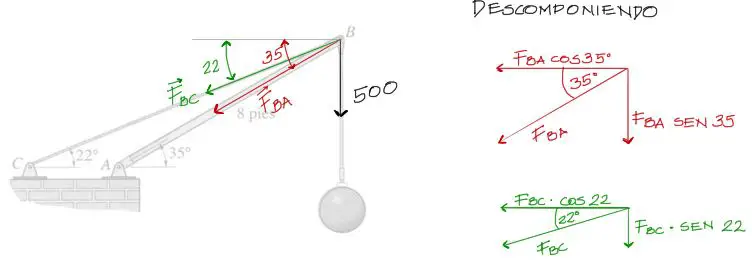
Además, para poder realizar la suma de fuerzas en X y en Y, se pueden descomponer estas dos fuerzas.

Luego, realizamos la sumatoria en ambas direcciones, para obtener:

Este es un sistema de dos ecuaciones con dos incógnitas. Reordenando términos y escribiendo estas ecuaciones en forma matricial se tiene la matriz mostrada a continuación. Resolviendola se obtienen los resultados de las incógnitas:

Vídeo

Si deseas la explicación en vídeo, la puedes ver a continuación

FIN