Enunciado

A continuación se explica la manera de obtener inercias de la figura mostrada

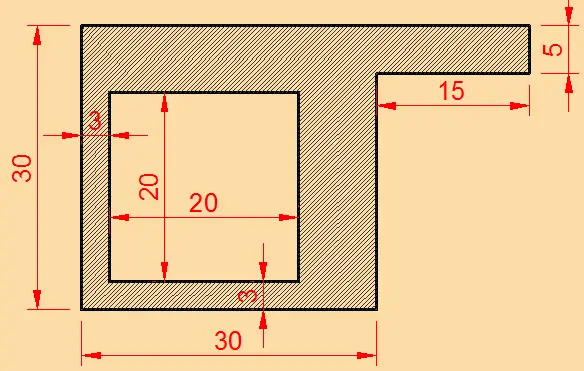Al contener la figura un hueco de 20×20 unidades, se debe considerar el área como negativa. Se verá esto en la tabla del desarrollo del problema más adelante.

Solución.-

a) Inercia Ix, Iy, Ixy, de figura compuesta

Primero se debe dividir la pieza en elementos rectangulares. La alternativa más conveniente se conforma de dos rectángulos positivos y un hueco negativo:

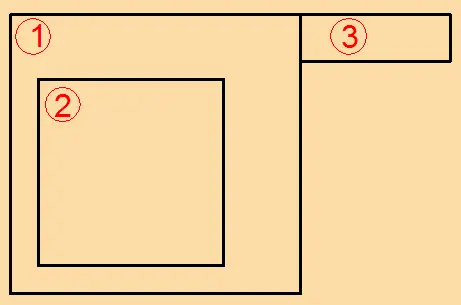Luego se deben encontrar los centroides de estos tres elementos. Para esto ubicamos un sistema de referencia en la esquina inferior izquierda (puede ser cualquier otra). Los centroides están acotados de verde.

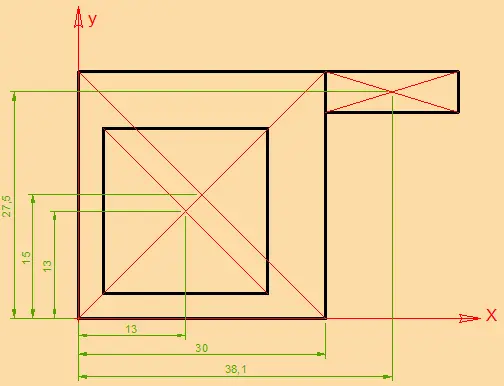Las áreas de los tres rectángulos junto con sus centroides se acomodan en una tabla, donde posteriormente se obtiene el centroide de toda la figura mediante:

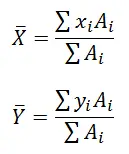Entonces se tiene, en tabla:

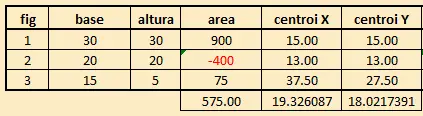Notar que el área de la figura 2 es negativa.

Posteriormente se puede comenzar a encontrar las intercias Ix, Iy y Ixy de los tres rectángulos. Sin embargo conceptualmente la inercia Ixy de un rectángulo respecto de su centroide vale cero.

Se tiene entonces:

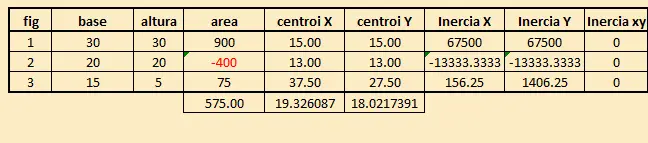Donde Ix = bh³/12

Iy = b³h/12

Luego se deben calcular los brazos de los centroides de cada figura al centroide de la figura compuesta. Estos brazos los denominaremos dx, y dy.

por ejemplo para la figura 1:

el brazo dx = 15-19.326087=-4.326

el brazo dy = 15-18.021739=-6.326

Se repite el mismo procedimiento para los otros dos rectángulos, obteniéndose finalmente:

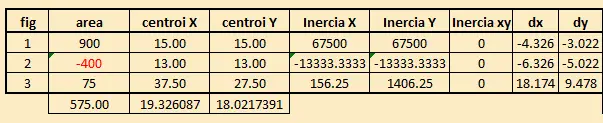Luego se deben calcular las inercias trasladadas de todas las figuras. Para esto debemos aplicar la fórmula de traslación de inercias:

Ix(trasladada) = Ix + A*dy²

Iy(trasladada) = Iy + A*dx²

Ixy(trasladada) = Ixy + A*dx*dy

Aplicando las fórmulas a la tabla se tiene:

Con lo que concluye la etapa de cálculo de inercias respecto a los ejes horizontal y vertical.

b) Inercias principales de la figura compuesta:

Para encontrar estas inercias se deben aplicar las fórmulas de rotación de inercias o aplicar el círculo de Mohr. Se ejecutarán ambos procedimientos.

Para encontrar las inercias principales mediante fórmulas se debe aplicar las siguientes:

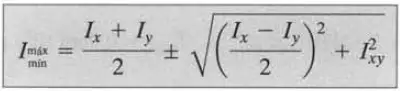
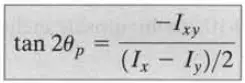Donde la primera fórmula se refiere a las inercias principales Máxima y Mínima, y la segunda fórmula se refiere al ángulo que se debe rotar la figura en sentido antihorario para obtener estas inercias máxima y mínima.

Aplicando ambas fórmulas se obtiene:

Imin = 53927.63

Imax = 86444.29

El ángulo de rotación de la figura para obtener estas inercias es:

θp= 23.7246°

Si representamos todo el análisis hecho hasta ahora en el círculo de Mohr, se tiene lo siguiente:

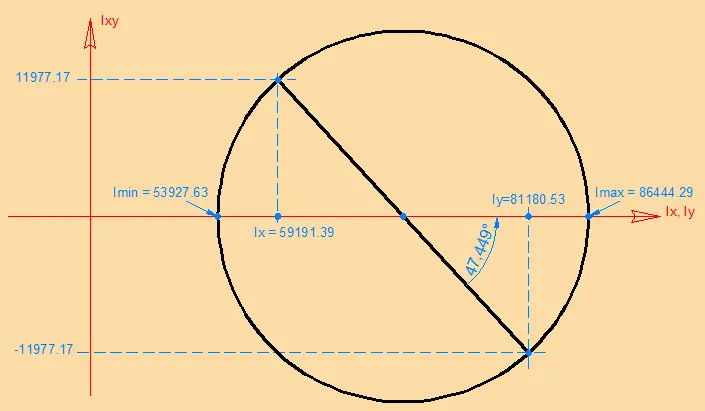Se puede apreciar del gráfico que para obtener las inercias principales I min y Imax se debe rotar el círculo de Mohr un ángulo de 47.449°, por tanto 2θp = 47.449. De donde θp=23.72, igual que el resultado analítico.

La figura rotada respecto de su centroide, para obtener las inercias máxima y mínima y además para que se anule el producto de inercia Ixy se verá de la siguiente manera:

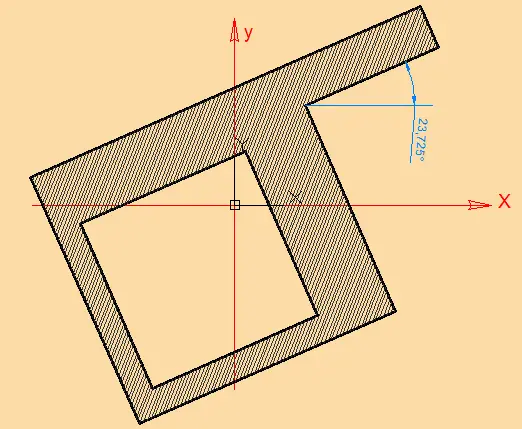Para un análisis más detallado del ejercicio, puedes descargar el archivo en excel haciendo click Aquí