Teoría
La teoría de solicitaciones de placa para una losa son complejas de resolver por métodos clásicos de ecuaciones diferenciales. Sin embargo los métodos numéricos se han vuelto el método de preferencia para encontrar estas solicitaciones.
Sin embargo, hay situaciones donde necesitamos solicitaciones de placa inmediatas para verificaciones rápidas en obra, y es ahí donde entran métodos simplificados de análisis y obtención de estas solicitaciones.
Método de Coeficientes
El método planteado acá corresponde al método de Marcus, publicado el año 1963, pero que se sigue usando hoy en día, especialmente en la materia de hormigón armado en pregrado, por ser un método sencillo de entender.
El método consiste en obtener unos coeficientes de tablas a partir de la relación del lado corto sobre el lado largo de una losa rectangular y a partir de la configuración de apoyos.
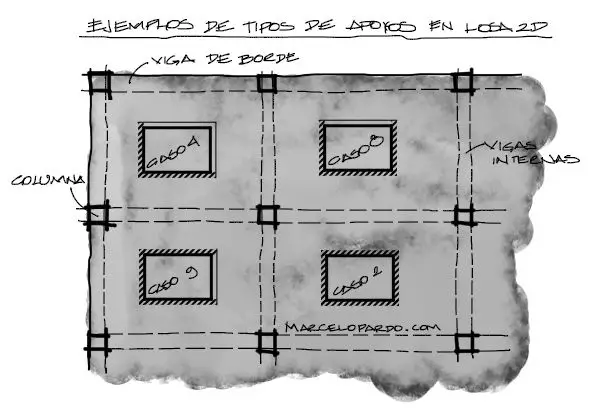
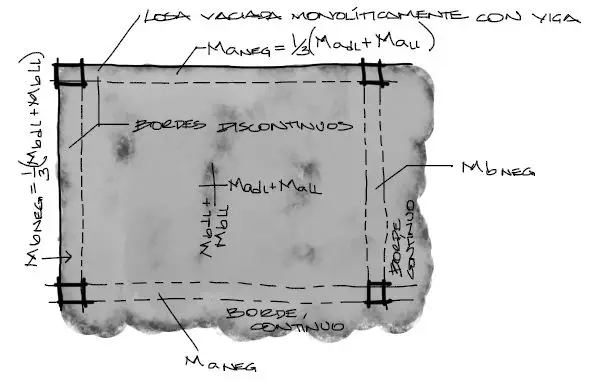
Así, si se tienen paños de losa como los mostrados arriba, se decide si cada paño tiene bordes contínuos o discontinuos (de borde) en función a si esta losa está conectada en una cara a otra losa o termina en viga. Entonces el dibujo de empotramiento no quiere decir necesariamente que la losa esté empotrada sino que tiene continuidad con un paño aledaño.
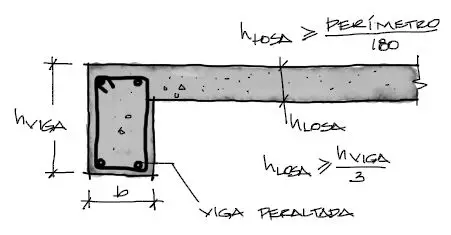
Para que el método tenga validez y para que la losa se considere apoyada en todo su borde, las vigas deben tener una altura por lo menos tres veces mayor que la losa, y la losa una altura mínima igual al perímetro del paño dividido entre 180.
Procedimiento
Momentos flectores
Lo primero que se debe obtener para un paño de análisis es la relación del lado corto «la» entre el lado largo «lb». A partir de este valor obtenido «m» conoceremos la fila a la que corresponde nuestra losa de análisis en las tres siguientes tablas. Si «m» estuviera en un caso intermedio entre dos valores de la tabla, lo más correcto es realizar una interpolación. En función al tipo de continuidad de la losa ingresamos a la columna correspondiente entre los casos 1 a 9.
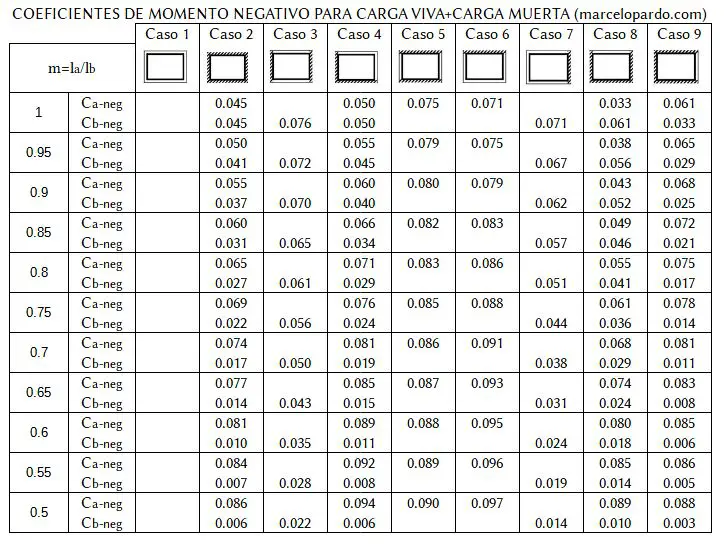
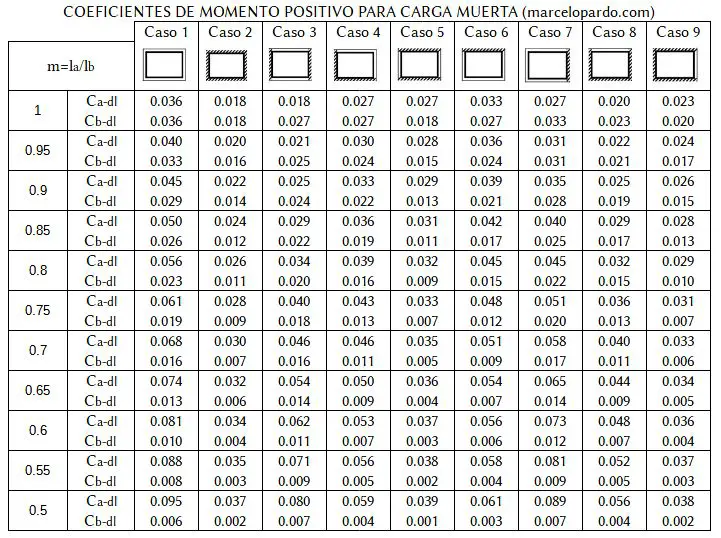
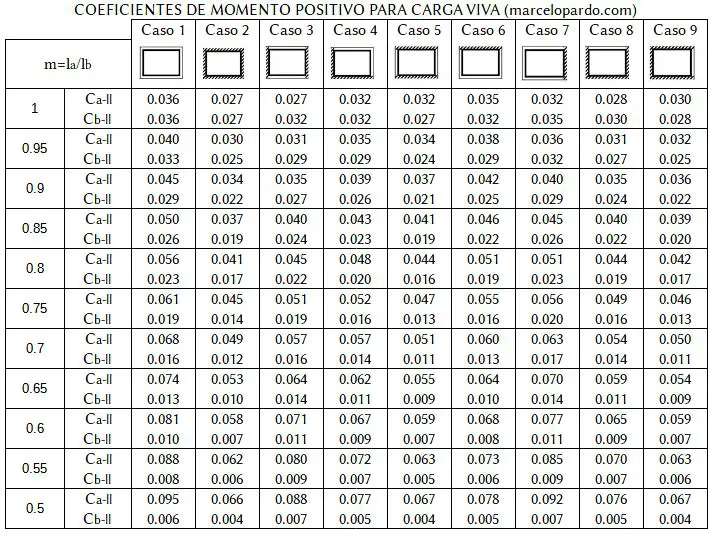
De cada tabla obtendremos un coeficiente Ca y Cb. Los subíndices «neg», «dl» y «ll» correponden a «negativo», «carga muerta» y «carga viva» respectivamente. Estos coeficientes debemos multiplicarlos por la carga y la luz al cuadrado la² y lb² respectivamente:
Ma corresponde en todos los casos al momento en la dirección más corta y en general siempre será el momento más grande. Mb corresponde al momento en la dirección más larga.
Para momentos negativos, el apoyo discontinuo tendrá un valor de cero si la losa está apoyada sobre mampostería o cuando la losa no está vaciada monolíticamente con el elemento de apoyo. Si la losa está vaciada monolíticamente con la viga o el muro, se puede incorporar un momento negativo en este apoyo igual a un tercio del apoyo positivo para esa dirección de análisis:
Cortantes
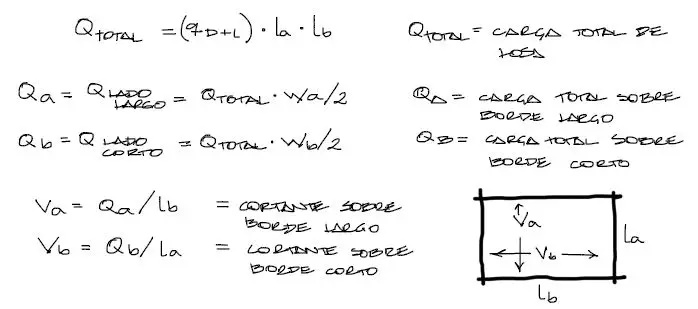
Para obtener los cortantes en cada borde, se aplican los coeficientes de la siguiente tabla. Esta misma tabla sirve para conocer las reacciones totales o por metro lineal de la viga hacia la losa.
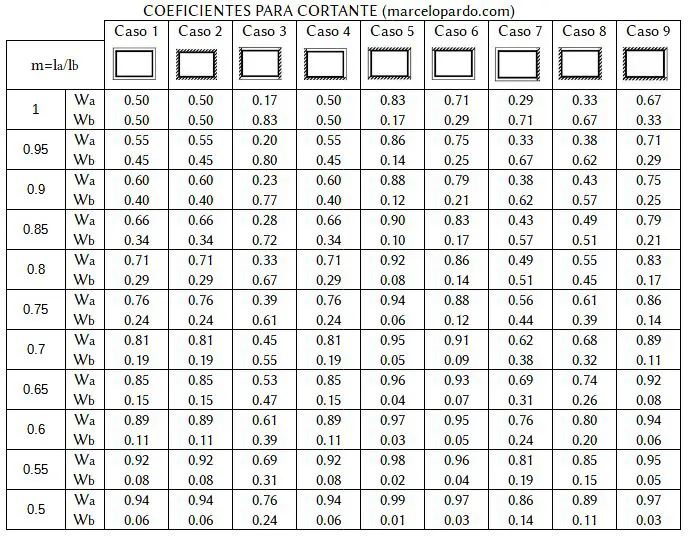
El uso de los coeficientes de esta tabla es similar al de las tablas anteriores.
Wa y Wb corresponde al porcentaje de carga sobre el lado largo y sobre el lado corto respectivamente. A partir de este razonamiento:
Programa y ejemplo
En el enlace siguiente elaboré un programa que hace todo este cálculo automáticamente. Un ejemplo detallado del uso de estas tablas lo elaboraré en la publicación siguiente.
Ejemplo de Solicitaciones en Losa en 2Dir
Programa de Solicitaciones en Losas
autor: Marcelo Pardo
