
Datos del problema
En una anterior publicación se realizó el diseño de una zapata a flexión (IR AL ENLACE DE ESA PUBLICACIÓN).. A partir de ese análisis se pudo determinar la cantidad de acero en la cara inferior de la zapata y también la altura de la zapata.
El análisis quedó de la siguiente manera. Altura total de la zapata de 65cm y 17 barras de acero de 16mm en cada dirección.
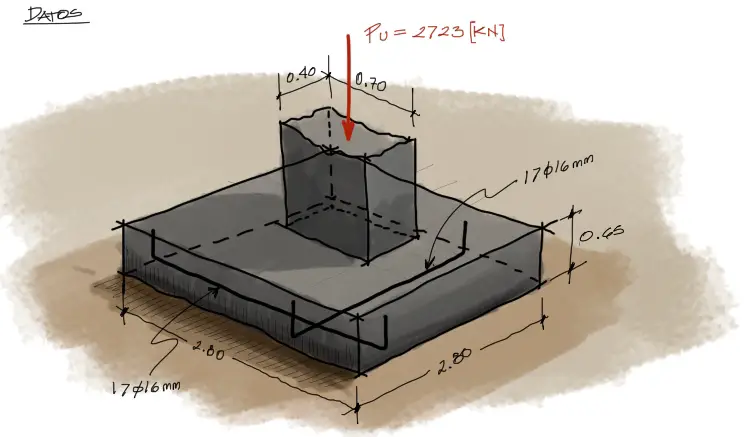
Sin embargo se deben realizar un par de verificaciones más para estar seguros que la zapata no fallará por el efecto de cortante.
Existen dos tipo de análisis que deben realizarse. El primero es el cortante en una dirección o en una cara, y el segundo es el cortante por punzonamiento.
Cortante en una dirección
Cortante solicitante
Cerca de las caras de la columna se produce un efecto de cortante muy grande producto de la reacción del suelo hacia la zapata. Si la fuerza cortante Vu es muy grande, producirá en el hormigón una falla a 45° en cualquiera de los lados de la columna como se muestra en la siguiente imagen.
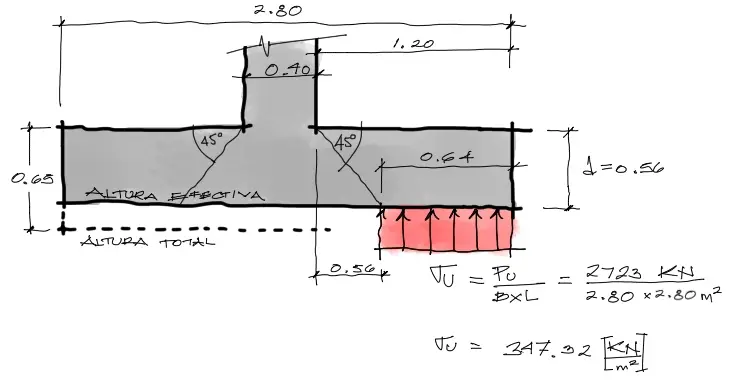
La proción de esfuerzo responsable de este fenómeno es el pintado de rojo. La magnitud de este esfuerzo corresponde al esfuerzo producto de la carga a la zapata dividida entre la superficie de contacto, que da como resultado un esfuerzo de 347.32 KPa. Debemos tomar en cuenta que como estamos en el campo de análisis del concreto, se debe utilizar la carga Pu mayorada y no así Pserv.
Este esfuerzo obviamente está distribuido debajo de toda la zapata, sin embargo solamente el esfuerzo que cae en la aleta de la zapata es la que produce el cortante de falla Vu.
El ancho de este esfuerzo en rojo se encuentra a partir de geometría, donde se proyecta a partir de la cara de la columna una distancia horizontal igual al peralte efectivo “d” de la zapata. A partir de esa cota de 0.56 horizontal, el restante 0.64m es el ancho del esfuerzo que produce Vu.
La superficie de falla puede verse mucho mejor en la siguiente imagen:
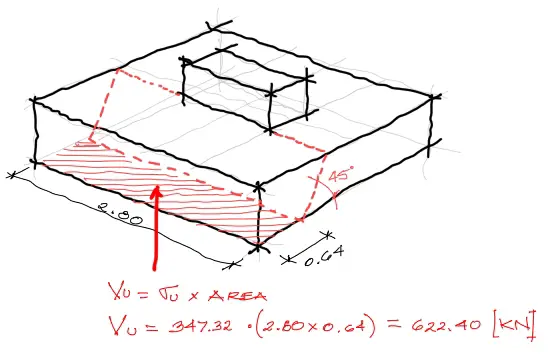
En este análisis se asume que la superficie de falla está ubicada en la cara más desfavorable. Si se hiciera el mismo análisis en el ancho de ala de 1.05m en vez del ala de 1.20m se obtendría un cortante solicitante más pequeño.
Para obtener el cortante de falla Vu, solo se debe multiplicar el esfuerzo de contacto entre el suelo y la zapata por la superficie achurada. Los 622.40 están en unidades de fuerza.
Cortante resistente
En el anterior subtíulo se calculó el cortante que produce la falla. En este apartado calcularemos la resistencia al cortante que proporciona el hormigón.
Tanto en el caso de muros, zapatas y losas, se busca que el cortante que llega a estos elementos sea completamente resistido por el concreto y no por acero. Esto se debe a que es muy complejo fabricar estribos o amarres verticales para elementos tan extensos y resulta más económico y práctico incrementar el espesor de la losa en caso de que la resistencia a cortante de la losa no sea suficiente.
Es en este sentido que el cortante resistente ϕVn = 0.75*(fc)^0.5*b*d está solo en función a la resistencia del concreto y de las dimensiones de la sección transversal.

En este caso la sección transversal está generada por el ancho de la zapata “B” y la altura efectiva “d”. La fórmula mostrada arriba es empírica y está en unidades de MPa, MN, m. El factor de reducción de resistencia ϕ es de 0.75 para cortante y todas las demás variables son conocidas.
El resultado obviamente lo obtenemos en MN que convertidos a KN se vuelve 898.18 KN que es mayor al cortante solicitante de Vu=622.40KN por tanto la sección de la zapata resiste al cortante Vu.
En caso de que la sección tuviera una resistencia al cortante menor que 622.40KN, la mejor alternativa es incrementar la altura de la zapata. Este incremento puede ser escalonado solo cerca de la columna o puede ser un incremento gradual, como de una zapata acartelada.
Cortante por Punzonamiento.
Cortante solicitante
El cortante por punzonamiento es un tipo de falla que se produce en forma de cono producto de la carga de la columna hacia el suelo. Esta superficie de falla se muestra en la figura siguiente.
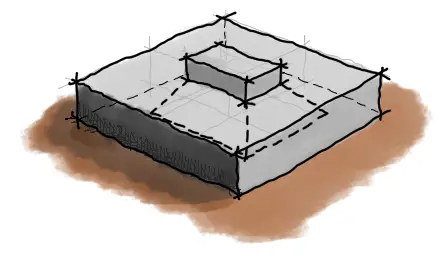
Pues bien, existe un cortante “Vu” solicitante que no es igual a la carga Pu. Es algo menor. Esto se debe a que la fuerza cortante Vu que genera la falla es producto del esfuerzo entre suelo y zapata en el perímetro de la zapata fuera del cono mostrado.
La superficie de contacto de este perímetro está mostrada en la siguiente imagen.
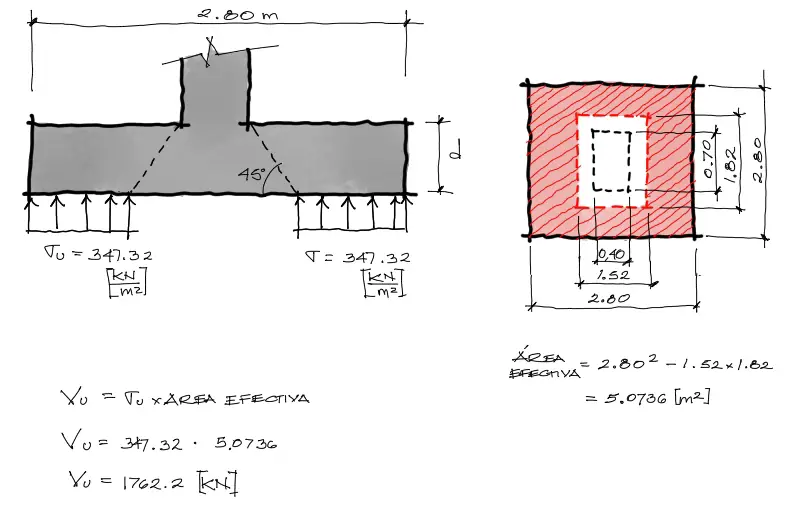
Al igual que en el cortante en una dirección, se puede obtener la base del cono sumando al ancho de la columna en cada lado, una magnitud igual al doble de la altura “d”. Un “d” a cada lado. El área efectiva achurada de rojo es de 5.07m2 que multiplicada por el esfuerzo de contacto entre la zapata y el suelo da un cortante Vu = 1762.2 [KN].
Cortante Resistente.
Es un tanto complicado conocer la superficie de falla exacta “en cono” producto del punzonamiento. Es por eso que la norma indica que la superficie resistente ϕVn a punzonamiento puede asumirse prismática, como se muestra en la siguiente imagen.
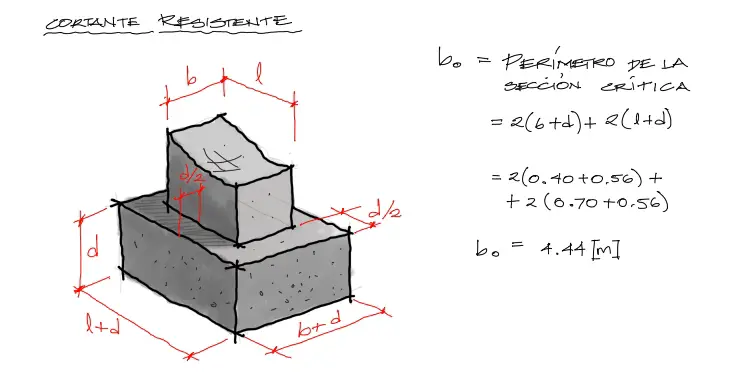
Esta superficie resistente se calcula a una distancia de d/2 alejada desde las caras de la columna. el perímetro de esta superficie de falla se denota por “bo” y en este caso vale 4.44m.
Luego, la norma ACI 318-14 indica que son tres fórmulas las que determinan el esfuerzo resistente a cortante de la zapata:
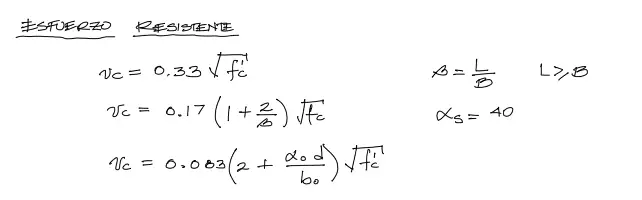
De estas tres fórmulas se escoge la que de el menor esfuerzo como esfuerzo resistente del concreto sometido a punzonamiento.
El parámetro Beta se calcula como la división entre L y B. El parámetro Alfa-s puede tomar tres valores. 20 cuando la columna cae en la esquina de la zapata, 30 cuando la columna cae en el borde de la zapata y 40 cuando la columna es concéntrica con la zapata.
Reemplazando todos los valores se tiene lo siguiente:
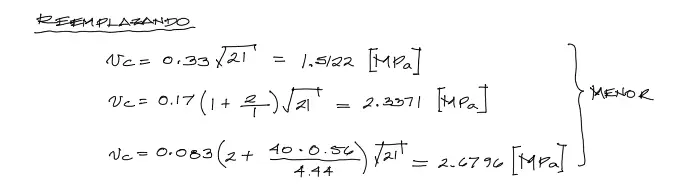
De estos tres valores obtenidos en [MPa] se escoge siempre el menor. Debemos notar que esta resistencia está en unidades de esfuerzo, y para convertirla en unidades de fuerza debemos multiplicarla por la superficie de falla, de la siguiente manera:

En las fórmulas anteriores además de multiplicar el esfuerzo vc resistente por la superficie resistente bo*d se debe multiplicar esta resistencia ϕVn por el factor ϕ=0.75.
En este caso el cortante resistente ϕVn = 2820 KN es mayor al cortante por punzonamiento solicitante igual a Vu=1762 KN. Por tanto la resistencia a cortante ϕVn soporta el cortante solicitante.
Conclusiones
Con esto termina el análisis del diseño de una zapata. En caso de que alguna de estas verificaciones no se cumpla, como indiqué antes, la mejor solución es incrementar la altura de la zapata ya se en forma escalonada o acartelada. También puede incrementarse la altura de toda la zapata por igual, pero esta solución puede no ser la más económica.
autor: Marcelo Pardo
Y PARA EL CASO DE ZAPATAS EXCÉNTRICAS Y ESQUINADAS COMO SERÍA EL ANALISIS
Buenas tardes colega, el cortante por punzonado aplica para losas de fundación? o solo para zapatas?
Andres, buena noche. Aplican las mismas fórmulas para losa de fundación. De todas maneras sucando la losa de fundación tiene vigas que llegan a la columna, yo le otorgo toda la resistencia a cortante a las vigas y no a la losa
Y una consulta mas ingeniero. Como seria la superficie de falla para una columna “L” y “T” para hacer la verificaciones correspondientes
Buenas tardes ingeniero, tengo una conulta. Que pasa si la superficie de falla que le da como resultado 622.40 [KN], no hubiera, entoces daria cero?, si fuera asi entonces el cortante resistente en una cara pasaria asi my facil?, si pudiera ofrecer una explicacion. Muchas gracias
Buenos días Marcelo, quiero felicitarlo por blog y los videos, son sumamente pedagógicos, quería consultarte si en algún momento podrás hacer un vídeo sobre losas de cimentación, acá en mí ciudad se utilizan mucho, pero no e encontrado ningún material claro sobre cómo realizar el cálculo. Desde ya muchas gracias
Gustavo, puedo realizar ese video, sin embargo tendría que formar parte de un curso, pues es bastante largo el proceso de cálculo
Y en el caso de zapatas combinadas cómo se usarían las fórmulas??
Escribiré al respecto José. Buena sugerencia
buenas tardes ingeniero, felicitarlo la verdad muy bueno el material compartido y agradecerle por los conocimientos que nos brinda. Megustaria que nos explique cual es la diferencia entre las fallas por cortante que se presentan en el diseño de fundaciones, y cual es la mas critica . gracias
Iran, la más crítica sin duda es la falla por punzonamiento. Es abrupta y sin pre aviso
Hola ing buenos días.
En el caso de que la zapata sea excéntrica, en cada dirección tendríamos 2 superficies de falla. Supongo que debería hacerse a ambos lados del pilar y analizar el más desfavorable, entiendo que de el mismo modo que lo has realizado en la dirección más desfavorable, pero, en este caso, eligiendo un área de la misma dirección.
Me encuentro con una zapata con una diferencia muy evidente a ambos lados del pilar ( es casi medianera) por lo que en un lado de ellos la falla se “sale” de la zapata. Como se consideraría? También, , como se considera el área a cortante en una zapata medianera. Y de esquina?
gracias
Armando buenas tardes. mmmm la verdad no entendí muy bien la consulta. 🙁
Ing. buenas noches, en primer lugar lo felicito por su trabajo, soy seguidor de su canal de youtube desde hace tiempo y me ha servido mucho para aclarar temas que no entendía totalmente.
Le agradecería que me ayude con respecto a la siguiente duda: he visto zapatas en las que la distancia medida de la cara de la columna a la cara de la zapata es menor que el peralte efectivo, en ese caso, ¿cómo se haría la verificación por corte en una dirección?
¡Saludos desde Perú!
Tery buen día. En esos casos la zapata no fallará a cortante por ningún motivo. básicamente lo que tienes de zapata es un cubo o dado que se comporta casi enteramente a compresión. para evitar que la zapata se abra en la base hace falta solamente armadura mínima por retracción ya que se trata de una masa de hormigón muy grande.
También puede analizarse por biela-tensor para estudiar sus esfuerzos internos
Hola ingeniero, en primer lugar me gustaría felicitarlo por la forma sencilla que tiene para explicar los conceptos y cálculos de las estructuras con un nivel de detalle exquisito!! Si bien no coinciden algunas cosas con el reglamento de mi país (ARGENTINA), me sirve mucho la teoría, porque pude comprender cosas que no entendía en mis apuntes.. La explicación teórica y práctica es algo que nuestros profesores no pueden conseguir.. Una duda que estoy teniendo respecto a este tema, es que se me hace muy similar el corte y punzamiento. No entiendo bien en que se diferencian particularmente, ya que los esquemas son similares. Muchas gracias y saludos
Martin buen día.
La diferencia consiste en que la falla de cortante simple se hipotetiza a lo largo de una sola cara. o sea, la falla es recta y no rodea a la columna, como en el caso del punzonamiento
Buenas noches ingeniero. Gracias por tan valioso aporte y excelente explicación.
Respecto al Área Efectiva en lugar de 1.52*1.82 ¿No serían los valores 0.96*1.26?
Es decir, yo creía que era un “d/2” a cada lado de los lados de la columna.
Saludos ingeniero.
Miguel, lo reviso. Eres mi editor oficial!!!
Bueno ya lo revisé.
Para conseguir el perímetro “bo” si se debe considerar por simplicidad d/2 a cada lado de la columna. Pero al igual que en vigas, se puede truncar el diagrama de cortante a una distancia “d” desde la cara de la columna. En este caso pasa una cosa similar. Al fallar la zapata en forma de cono, la superficie de falla que genera el esfuerzo de falla está alejado una distancia “d” desde las caras de la columna como se muestra en la imagen de la izquierda.
Espero se haya entendido la explicación 🙂
Mas claro no canta un gallo…conceptos que antes eran tan abstractos ya son clarisimos…muchas gracias ingeniero por compartir sus conocimientos
Muchas gracias jugaleano por dejarme tu parecer. Un fuerte abrazo!
Buen día ingeniero, muchas gracias por el tema compartido, me es de mucha ayuda. Me gustaría saber la Normativa que usa, o algún autor de referencia, para comprender más de las fórmulas que ud. utiliza. Saludos!.
Nilsson buenas tardes! te comento que para todo utilizo la norma ACI 318-14
Buenas tardes Ing. Marcelo lo felicito por que tiene la facilidad de expresión para explicar muy bien, buen vídeo.
Muchisimas gracias Jairo!!! gracias por visitar mi página web
Buenos días ingeniero, felicitarlo y agradecerle por los conocimientos que nos brinda. Me gustaría que nos diera su opinión sobre el tema no se si controvertido de él recalce de zapatas y todos los pro y contras de los métodos que hubieren y si no es mucho pedir un poco de teoría matemática sobre estos. Gracias y siga así. Atentamente un fan 😀
Edu buen día! El tema de recalce es de hecho muy interesante. gracias por sugerir el tema. Nunca hice uno en lo personal, pero sin duda lo anotaré para investigar al respecto