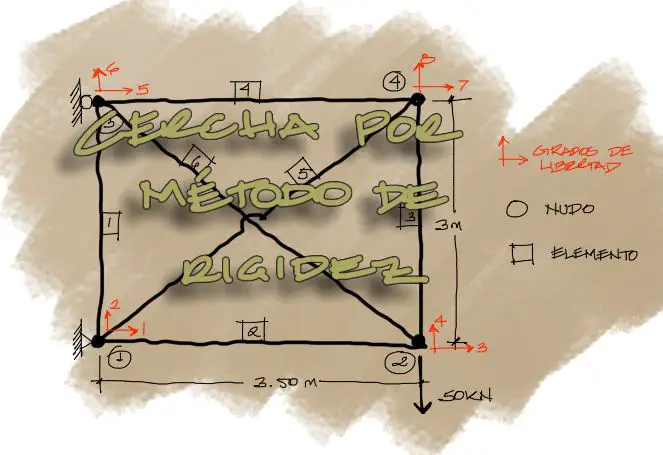
Planteamiento

El siguiente ejemplo es una cercha o armadura calculada mediante el método matricial. Este método es conocido por su versatilidad al momento de calcular armaduras hiperestáticas o cuando se tenga un gran número de elementos en la estructura.

La estructura que calcularemos es la siguiente:

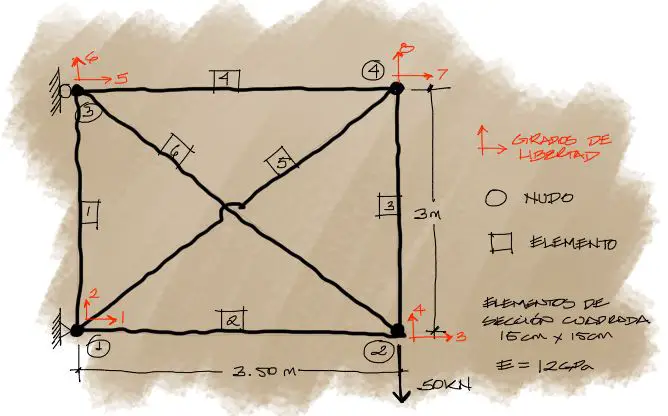
Solución

Matriz de rigidez para un elemento

La teoría del método matricial se puede encontrar en muchos libros de análisis estructural, pero básicamente se resume en el ensamblaje de matrices individuales que contengan toda la información de esfuerzo – deformación de cada elemento. La matriz de cada elemento que contiene estas propiedades se conoce como Matriz de rigidez [k], y es la mostrada a continuación

donde:

• E = módulo elástico de cada elemento
• A = Superficie de la sección transversal de cada elemento
• L = Longitud de cada elemento de barra
• α = ángulo de cada barra medida desde el eje x positivo. El ángulo es antihorario positivo

Reemplazo de datos para cada elemento

Una vez reemplazados los datos de cada matriz de rigidez, para cada elemento de la cecha (que se ve en la planilla excel adjunta).

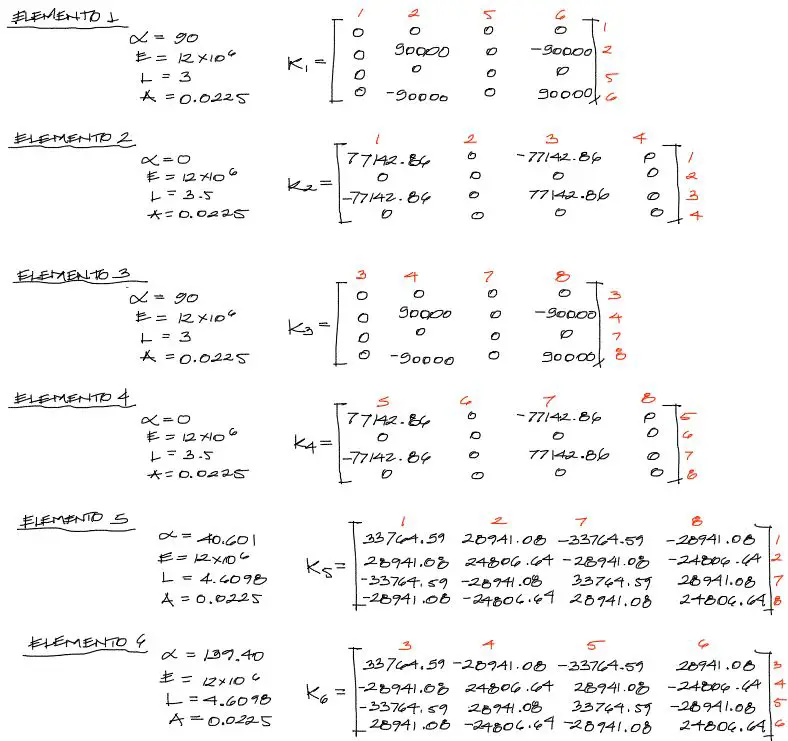
Posteriormente se ensambla la matriz de rigidez global compuesta de cada una de las matrices elementales. La dimensión de la matriz de rigidez global es la misma que la cantidad de grados de libertad que existan en la estructura. En este caso se tienen 8 grados de libertad, por tanto la matriz de rigidez será de 8×8.

Si notas en cada matriz de rigidez de cada elemento, existe la numeración encima indicando de que grado de libertad a qué grado de libertad va esa respectiva barra. Estas posiciones de la matriz de rigidez local se deben trasladar a la matriz de rigidez global. Si existen dos elementos cayendo dentro de la misma casilla en la matriz de rigidez global, entonces se suman.

Ensamblaje de la matriz Global

ensamblada la matriz de rigidez global se tiene entonces:

Teniendo la matriz de rigidez global, se conforma el sistema de ecuaciones siguiente:

Resolución del sistema de ecuaciones – Encontrando Desplazamientos

De este sistema de ecuaciones existen datos conocidos (que son las condiciones de borde del problema). Los desplazamientos de los grados de libertad 1, 2, 5 son conocidos e iguales a cero. Por otro lado la carga en el grado de libertad 4 es igual a 50 hacia abajo, por tanto negativa. Las cargas en los grados de libertad 3, 6, 7, 8 son nulas. Finalmente las reacciones serán incógnitas en los grados de libertad restringidos (desplazamientos = 0). Por tanto queda:

el siguiente paso consiste en anular filas y columnas de los grados de libertad restringidos (1, 2, 5)

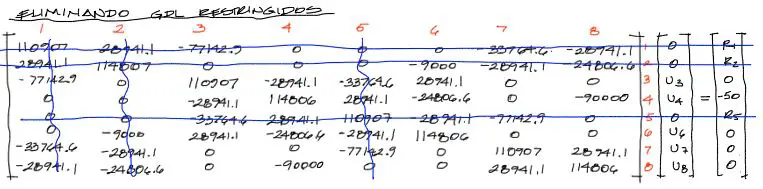
Anuladas estas filas y columnas queda el sistema de ecuaciones siguiente:

Multiplicando la matriz de rigidez invertida por las cargas, quedan los siguientes desplazamientos:

…que son los desplazamientos que faltaban conocer.

Reacciones en la cercha

Con estos desplazamientos ya se pueden conocer las reacciones del sistema de cercha. Para esto reemplazamos los desplazamientos en el sistema de 8×8 original, donde ya todos los desplazamientos son conocidos:

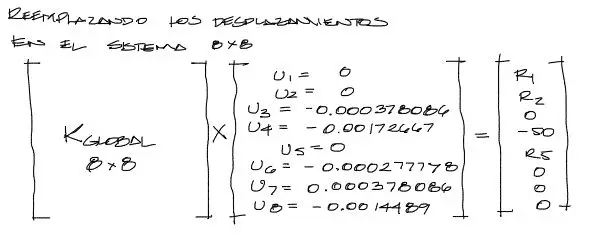
Luego de la multiplicación respectiva de la matriz de rigidez [k]*{u} queda:

que son las reacciones de los grados de libertad restringidos.

Con esto terminaría la primera parte de la resolución de una cercha por método matricial. Para encontrar las solicitaciones de cada barra se deberá seguir un procedimiento que explicaré en otro post.

Solicitaciones

Las solicitaciones de esta cercha se calculan a partir del procedimiento en EL SIGUIENTE ARTÍCULO

autor: Marcelo Pardo

→→→ SOLICITACIONES EN BARRAS – CONTINUACIÓN DE EJEMPLO →→→

← ← ← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS← ← ←