Pasos previos
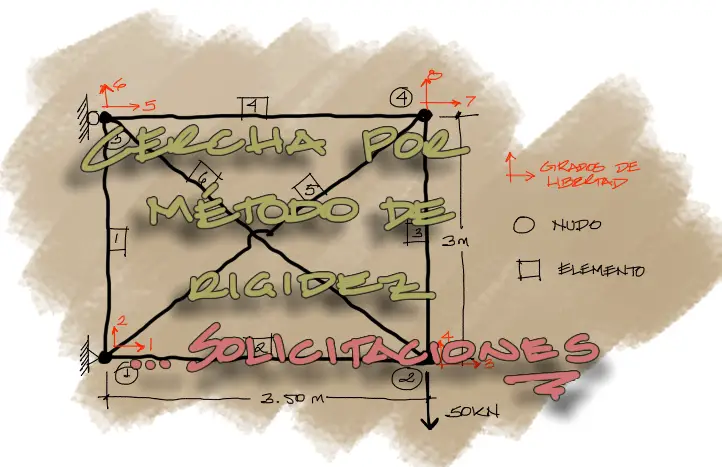
En el anterior artículo hemos resuelto los desplazamientos y las reacciones de la cercha mostrada en la imagen
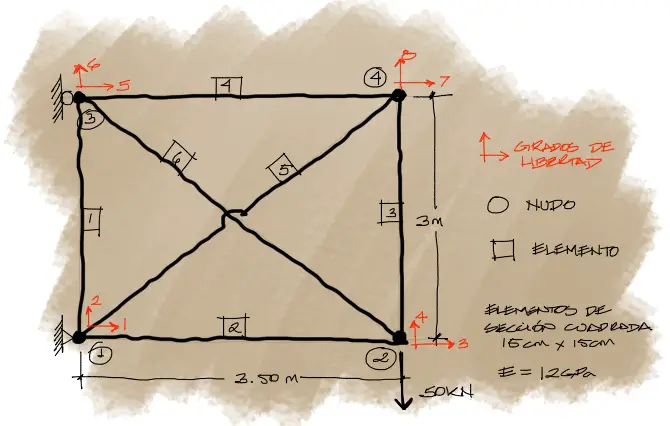
Sin embargo de muy poco van a servirnos los desplazamientos de los nudos de la cercha cuando el propósito final de muchos diseños estructurales consiste en el análisis de las solicitaciones de sus elementos para su dimensionamiento.
Es en este sentido que en esta segunda parte del análisis encontraremos las solicitaciones de los elementos.
Previa teoría
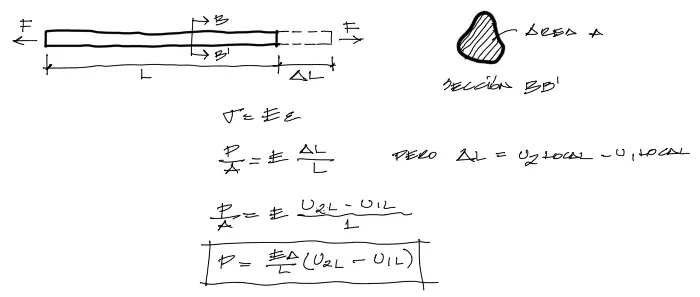
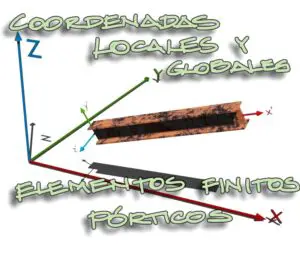
Cuando se tiene una barra con los desplazamientos en los extremos de los nudos en coordenadas globales, se pueden rotar estos desplazamientos para que los desplazamientos u1 y u2 locales se orienten en la dirección longitudinal de la barra, como se muestra en la imagen siguiente:
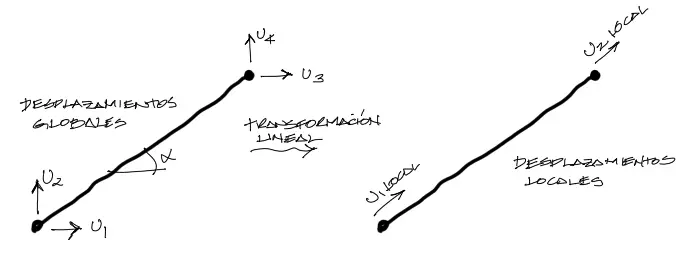
No se efectuará la demostración en este apartado. Basta mencionar que para lograr esto matemáticamente podemos multiplicar la matriz de transformación [T] por los desplazamientos en coordenadas globales. Así obtenemos los desplazamientos en coordenadas locales para cada barra.
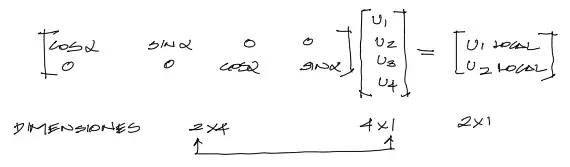
Obtenidos los desplazamientos en coordenadas paralelas al eje de cada barra, es fácil encontrar las solicitaciones de la barra en función a la resta de los desplazamientos locales. La resta de u2Local-u1Local es diréctamente la deformación de la barra “delta L”. Y por resistencia de materiales sabemos que la deformación unitaria de un elemento es deltaL/L. Por tanto podemos encontrar la solicitación F de la barra mediante:
Análisis de la barra 5
El análisis de las barras que tienen un ángulo de 0 grados respecto a la horizontal o 90° respecto a la horizontal siguen este mismo procedimiento y es aún más directo que cuando la barra está inclinada, por tanto no nos detendremos en esos elementos.
Enfoquemos nuestra atención a la barra 5, que está inclinada y cuyo análsis es más interesante. Los desplazamientos de sus nudos en coordenadas globales se muestra a continuación:
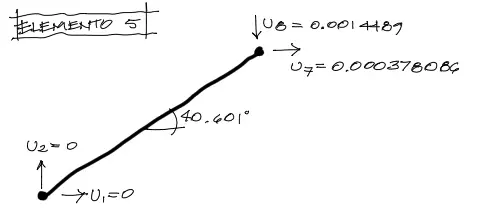
Aplicamos la transformación de los desplazamientos a coordenadas locales, y se tiene:
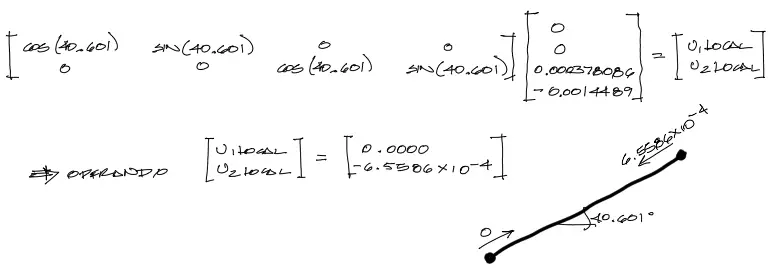
Finalmente aplicando las fórmulas de resistencia de materiales citadas arriba, obtenemos la solicitación axial de la barra:
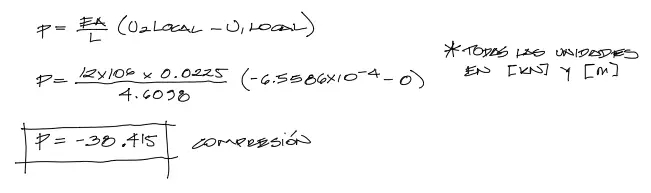
El valor negativo del resultado indica compresión en la solicitación de la barra.
De la misma manera pueden obtenerse las solicitaciones de todas las barras:
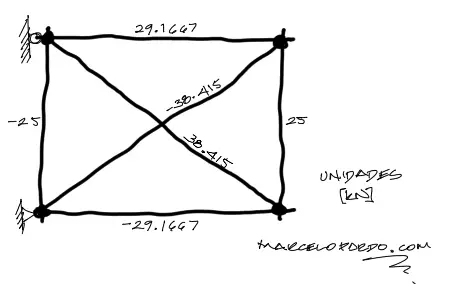
autor: Marcelo Pardo
← ← ← 1ra Parte – Ejemplo de cercha – Desplazamientos de nudos← ← ←
Magnífico. Excelente. Genial.