Vectores, matrices y tensores

Vector

Es necesario conocer la estructura de un vector, de una matriz y de un tensor si lo que uno quiere es guardar este tipo de elementos en Octave o en Matlab.

Un vector se puede definir como un arreglo de valores (numéricos) de una sola fila por un número mayor a uno de columnas o viceeversa

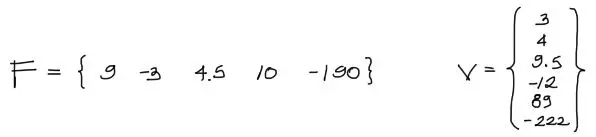
matriz

Consiste en un arreglo de varias filas y varias columnas de datos. Para propósitos de ingeniería en octave preferentemente los datos serán numéricos.

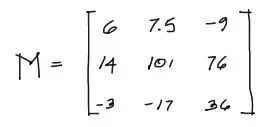
tensor

Se puede definir en términos coloquiales como una matriz de matrices. Es un arreglo que puede tener no solo filas y columnas, sino un elemento o dimensión adicional que me gusta llamar “hojas”. Por si acaso estoy utilizando términos coloquiales. En realidad al definir este tipo de elementos lo único que existen son dimensiones. Por ejemplo, un escalar es un tensor de dimensión cero. Un vector es un tensor de dimensión uno. Un vector es un tensor de dimensión 2, y una matriz de matrices será un tensor de dimensión 3. Podríamos seguir con tensores de dimensión 4, pero no hablaremos de ello ahora.

si queremos definir una matriz de matrices o un tensor de dimensión 3, podríamos imaginarlo de la siguiente manera:

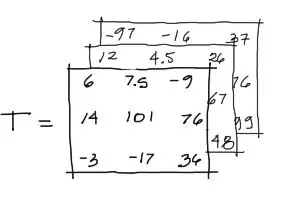
Definir estos elementos en Octave

Todas las líneas de código que se presentan aquí están escritas en un archivo .m y no en la terminal >>, pues es una buena práctica ordenar al programa todas las operaciones desde un archivo de texto como los archivos .m

escalar

Para definir un escalar, un vector o matriz, no necesitamos declarar la variable. En un archivo .m podemos simplemente escribir la variable y asignarle un valor mediante la asigación misma. Por ejemplo, si quiero que A valga 3, simplemente escribimos
A = 3
El punto y coma evita que el resultado de la asignación se escriba en la terminal.

vector

Si quisera asignar un vector a un variable F, como en el ejemplo de definición de vector, simplemente escribo en Octave:

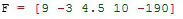
Otra manera de definir un vector fila es separando los términos mediante “,” como sigue

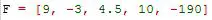
Cualquiera de las dos sintaxis sirve.
Si por ejemplo tuviera demasiados términos y quisiera continuar escribiendolos en una siguiente línea puedo utilizar puntos suspensivos:

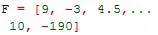
Y el resultado es exáctamente el mismo

Si el vector que quisieras definir fuera un vector columna, entonces existen diferentes maneras de declararlo. Una de las más sencillas es por ejemplo:

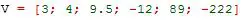
El punto y coma (;) dentro de los corchetes determina nueva fila. Por tanto el resultado se verá:

Otra manera de definir un vector columna es escribiendo todos los elementos en una sola fila y luego transponiendo este vector:

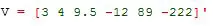
El apóstrofe (‘) indica que el vector debe transponerse, obteniendo nosotros el mismo resultado que en el anterior caso.
También puede escribirse el vector en columna, tal como quisieramos que se imprima, de la siguiente manera:

Y esto producirá el mismo resultado que en las anteriores sintaxis.
Si bien existe otra manera de guardar datos en una matriz y consiste en escribir el código de la siguiente manera:

Notarás que se han suprimido los puntos suspensivos para ir a la siguiente línea. Si bien esta es una práctica común dentro de los programas escritos en Octave y no genera ningún error, la práctica ordenada de escritura de código dicta mejor utilizar los puntos suspensivos.

Matrices

Siguiendo las mismas reglas que en el caso de Vectores, se puede escribir la matriz del ejemplo mostrado al comienzo del artículo de la siguiente manera:

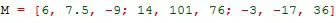
Las columnas se separan por (,) y para ir a la siguiente línea de matriz se separan filas con (;).
Sin embargo cuando se van a escribir matrices grandes es muy conveniente escribir las matrices de manera más ordenada como se muestra a continuación, escribiendo las filas de la matriz separadas también en filas en el archivo .m:

Finalmente, se puede también agrupar las filas como vectores independientes anidando vectores fila dentro de un vector columna. Sin embargo esta práctica no es tan comun como las dos anteriores:

Tensores

Aquí agregamos una dimensión más (o más si se quisiera) a nuestro arreglo, formando una matriz de matrices. En este caso se debe declarar cada “hoja” del tensor por separado de la siguiente manera:

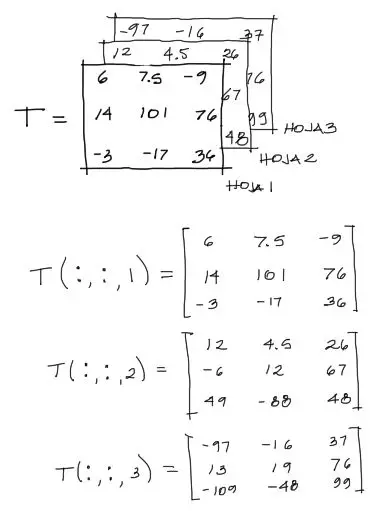
En la imagen mostrada, notas que el tensor T tiene tres dimensiones donde se definen las dimensiones de la siguiente manera:

T(filas,columnas,hojas)

Por tanto se puede ir almacenando cada hoja a la vez asigando por ejemplo la matriz de la hoja 1 a T(:,:,1) donde los dos puntos representan “todas las filas” o “todas las columnas” respectivamente.
En código tenemos:

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE OCTAVE – MATLAB←←←