…CUANDO TANTO EL ACERO DE COMPRESIÓN COMO DE TRACCIÓN FLUYEN

Pasos previos

Esta es parte de la demostración de las fórmulas para determinar la resistencia de una viga a flexión con acero de refuerzo a tracción y compresión.

A partir de los cálculos anteriores, estamos en la situación donde tanto acero a compresión como acero a tracción llegan a la fluencia.

As en fluencia y As’ en fluencia

Se ha comprobado en la anterior publicación que:

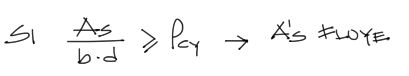
…y explicamos por qué a partir de esta condición el acero a compresión fluye. Mucho antes explicamos por qué llegados a este punto, el acero a tracción también fluye.

Dada esa condición, podemos trazar el siguiente dibujo esquemático, de los esfuerzos y fuerzas actuantes en la sección transversal:

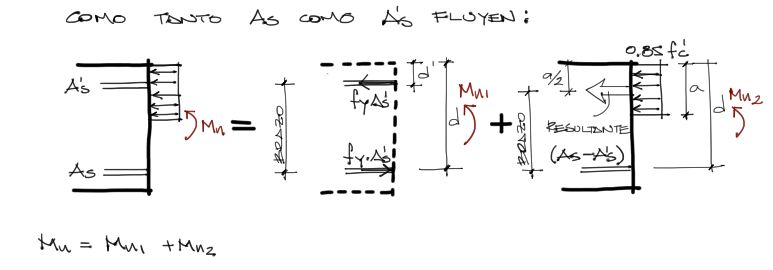
Tanto las fuerzas de tracción como de compresión corresponden a las secciones transversales por el esfuerzo en esas secciones. Los datos conocidos son:

Sección de acero a tracción As
Sección de acero a compresión As’
Esfuerzo de fluencia fy
Esfuerzo a compresión del concreto fc’
Ubicación de las posiciones de aceros d y d’ respecto a la fibra más comprimida

El único dato que falta conocer es la altura del bloque de compresión del concreto «a».

Para equilibrar el sistema, separaremos el brazo de fuerza (Mn1) generado por el par del acero a compresión As’ con una porción de As igual a As’, y por otro lado el momento de fuerza resistente (Mn2) generado por el restante de acero a tracción (As-As’) junto con el concreto. Recordemos que «Mn» quiere decir Momento Nominal, y se refiere al momento máximo resistente de la sección transversal antes de ser aplicados los factores de seguridad.

Mn1

La fuerza de compresión del acero As’ puede ser compensada perfectamente por una cantidad de acero a tracción en el equilibrio de fuerzas. Ambos generan un momento de fuerza resistente (par) a los momentos flectores solicitantes que puede calcularse a partir del brazo de fuerza entre ambas fuerzas de aceros, multiplicada por una de las dos fuerzas (en este caso escogeremos fy*As’):

Mn2

La fracción de acero a tracción (As-As’) que no es equilibrada por su contraparte de acero a compresión buscará el equilibrio en una cantidad de fuerza igual y contraria generada por el concreto. Sin embargo no conocemos la superficie de concreto que equilibra la tracción de (As-As’).

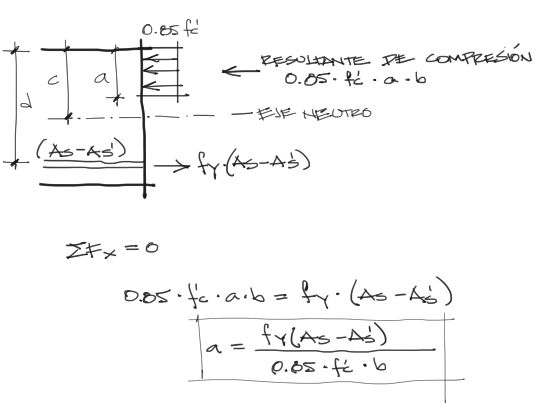
Esta superficie la podemos conocer despejando «a» de la ecuación de equilibrio de fuerza.

Con el valor de «a» conocido, podemos encontrar el brazo de fuerza o par Mn2 resistente generado por el acero (As-As’) junto con el bloque de compresión de concreto. El pivote podemos hacerlo respecto al centroide del bloque de concreto o respecto al centro del acero a tracción. El resultado será el mismo.

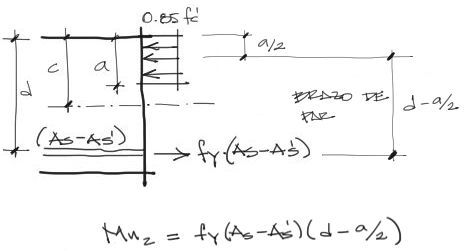
Momento nominal total

El momento nominal resistente total de la sección tansversal es el aporte del Mn1 y Mn2.

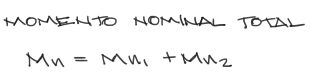
Momento de diseño

El momento de diseño es igual al momento máximo resistente Mn multiplicado por un factor de seguridad. Este factor de seguridad está en función a cuan dúctil es la falla de la viga. A la vez esta ductilidad se mide en función a cuánto se deforma el acero justo antes de la falla.

Si la deformación unitaria de acero a tracción es menor a fy/Es, la falla será frágil, por tanto ɸ=0.65. Si la deformación unitaria es mayor a 0.005, la falla será muy dúctil, y por tanto, ɸ=0.90. Para casos intermedios, se aplicará una transición. En fórmula: