Pasos previos
Esta es parte de la demostración de las fórmulas para determinar la resistencia de una viga a flexión con acero de refuerzo a tracción y compresión.
A partir de los cálculos anteriores, estamos en la situación donde el acero a compresión no fluye y el acero a tracción si fluye.
As en fluencia y As’ por debajo del esfuerzo fy
Se ha comprobado en la anterior publicación que:

…y explicamos por qué a partir de esta condición el acero a compresión no fluye. Además mucho antes ya habíamos visto que llegados a este punto, el acero a tracción fluye, debido a que la cuantía balanceada es mayor a la cuantía real de acero a tracción.
Bajo la mencionada situación de esfuerzos, podemos dibujar la sección transversal tanto en esfuerzos como en deformaciones:

Tanto las fuerzas de tracción como de compresión corresponden a las secciones transversales por el esfuerzo en esas secciones. Los datos conocidos son:
- Sección de acero a tracción As
- Sección de acero a compresión As’
- Esfuerzo de fluencia fy en tracción.
- Esfuerzo a compresión del concreto fc’
- Ubicación de las posiciones de aceros d y d’ respecto a la fibra más comprimida
En este caso no se conoce ni la altura del eje neutro “c” ni el esfuerzo de fluencia fs’ del acero a compresión.
Determinación de fs’ y c
De las deformaciones de la sección transversal, por triángulos podemos deducir que:
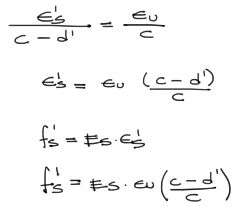
…donde fs’ está en función de puro datos conocidos excepto “c”, la altura del eje neutro.
Además por equilibrio de suma de fuerzas horizontales podemos escribir la igualdad:

donde podemos reemplazar fs’ en esta última ecuación a partir de la anterior.
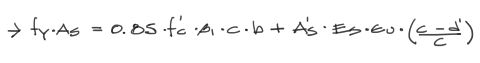
Si se desarrolla esta última ecuación con la única incógnita “c”, terminamos con una ecuación de segundo grado que deberá resolverse:

Se obtendrán dos soluciones, de las cuales el resultado de “c” que nos sirve es el que se encuentre entre 0 y h:

Momento nominal
El momento máximo resistente de la sección transversal se obtiene a partir de la suma de momentos de fuerza de todas las fuerzas actuando en la sección. Si hacemos pivote en el acero a tracción “As”, su fuerza no genera brazo y nos quedamos solo con los momentos de fuerza del hormigón a compresión y acero a compresión por sus respectivos brazos:
Momento de diseño ɸMn
El momento de diseño ɸMn es igual al momento máximo resistente Mn multiplicado por un factor de seguridad. Este factor de seguridad está en función a cuan dúctil es la falla de la viga. A la vez esta ductilidad se mide en función a cuánto se deforma el acero justo antes de la falla.
Si la deformación unitaria de acero a tracción es menor a fy/Es, la falla será frágil, por tanto ɸ=0.65. Si la deformación unitaria es mayor a 0.005, la falla será muy dúctil, y por tanto, ɸ=0.90. Para casos intermedios, se aplicará una transición. En fórmula:
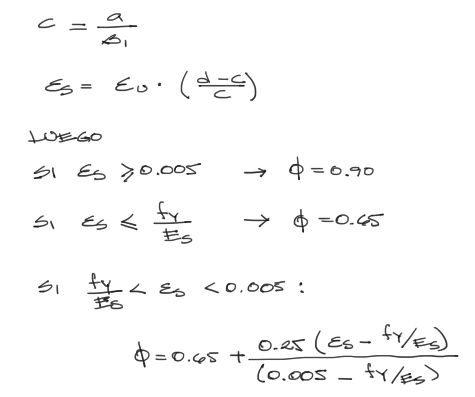
Es probable que ɸ esté muy cerca a 0.9 o que sea 0.9, dependiendo de cuanto fluya el acero a tracción durante la falla.
Diagrama de flujo y programa
El resumen en diagrama de flujo de todas las fórmulas encontradas se encuentra en el enlace:
DIAGRAMA DE FLUJO DE REVISIÓN DE RESISTENCIA DE VIGAS DE HORMIGÓN ARMADO SOMETIDAS A FLEXIÓN
El programa que te ayudará a resolver la resistencia de vigas con As y As’ conocidos está en el siguiente enlace:
PROGRAMA DE REVISIÓN DE RESISTENCIA A FLEXIÓN DE VIGAS DE HORMIGÓN ARMADO
autor: Marcelo Pardo