No fluye As / No Fluye As'

Pasos previos

Hasta aquí se hicieron dos verificaciones. La primera correspondiente a si el acero a tracción fluye o no. En esta parte de la demostración se verificó que el acero a tracción NO fluye.

la segunda verificación realizada corresponde a si el acero a compresión fluye. En función a la cantidad de acero a tracción real respecto a As_cy se verificó para esta parte de la demostración que el acero a compresión TAMPOCO fluye.

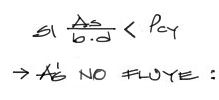
Equilibrio de fuerzas horizontales

En este caso, como no fluye ni el acero a compresión ni el acero a tracción, ambos esfuerzos de estas barras son desconocidos. Si trazamos la sección transversal con las deformadas de ambas barras, se pueden deducir los valores de las deformaciones ε y sus respectivos esfuerzos, en función de la altura del eje neutro (también desconocida aún):

A partir de este análisis, ahora tanto el esfuerzo de las barras de tracción fs como de compresión fs’ están en función de la altura del eje neutro «c».

Luego, si realizamos el equilibrio de fuerzas horizontales se tiene:

La ecuación de equilibrio tiene varios valores desconocidos, pero todos ellos (fs, fs’ y a) pueden escribirse en función de «c» como única incógnita. Realizando este reemplazo y deordenando términos, quedamos con una ecuación de segundo grado que puede resolverse fácilmente. De las dos soluciones de «c», la que esté entre cero y la altura de la viga es la solución correcta.

Equilibrio de momentos

Habiendo encontrado la altura del eje neutro «c», ya se tienen todos los datos para encontrar los momentos de fuerza resistentes de toda la sección. Para eso haremos pivote en el punto del acero de tracción (Aunque se puede escoger cualquier otro punto) y se calculan los momentos de fuerza aportados por el acero a compresión y por el concreto:

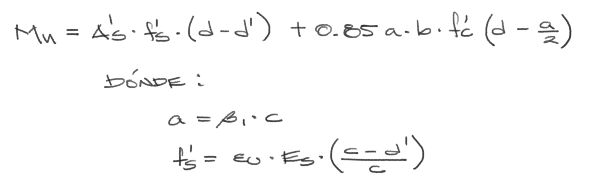
Mn es el momento nominal resistente de la sección de la viga cuando As NO fluye y As’ fluye. El último paso consiste en encontrar el momento de diseño de la sección transversal

Momento de diseño ɸMn

En un caso típico a flexión, el valor de ɸ es 0.90. Sin embargo debido a que en todos los casos de análisis el acero a tracción toma valores que no siempre son mayores a εs=0.005 (como el presente caso, donde el acero a tracción no fluye), se deben hacer las verificaciones pertinentes para saber si ɸ vale 0.90, si vale 0.65, o si está en una zona de transición entre ambos.

Para determinar el valor de ɸ aplicamos: