Enunciado
El problema pide encontrar el centroide de la figura sombreada siguiente:
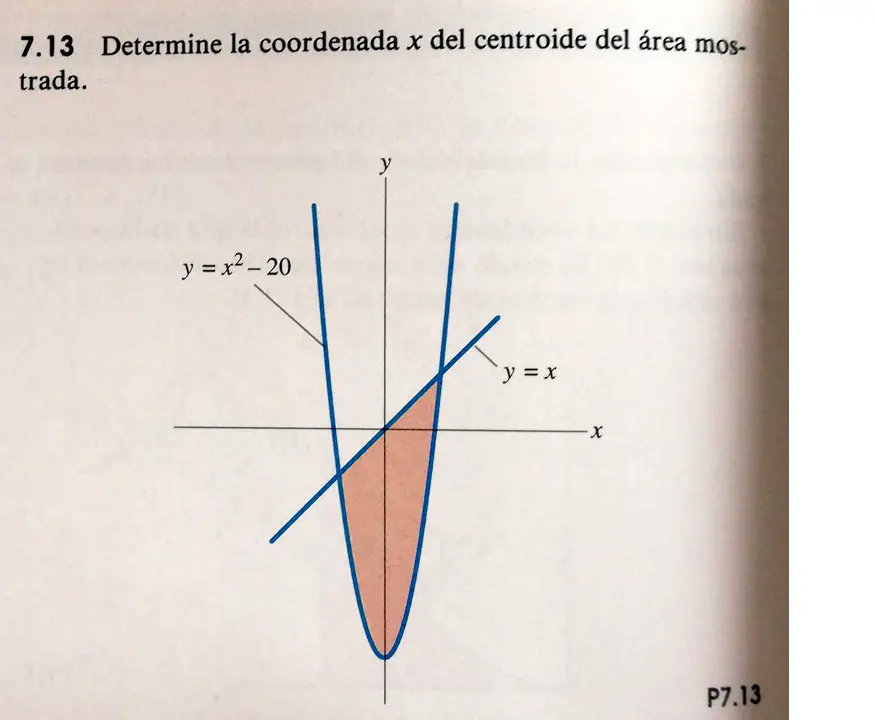
El problema se resolverá analíticamente y mediante el programa alternativo a Matlab llamado Octave, que utiliza los mismos archivos .m pero es completamente gratuito.
Solución Analítica
Para solucionar el problema de forma analítica se debe tener en cuenta el concepto de centroide tanto en X como en Y, que obedece a las siguientes dos fórmulas:
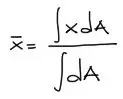
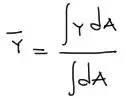
Entonces el procedimiento a seguir es el siguiente:
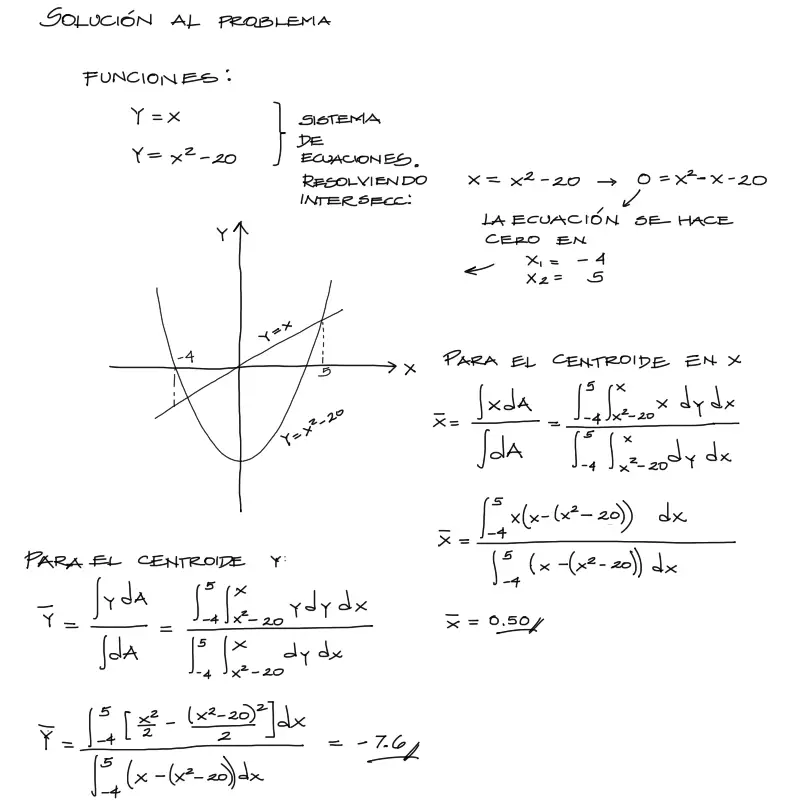
- Se encuentran los valores en X de intersección de las dos curvas
- Estos valores X1 y X2 serán los límites de integración para dx
- Los límites de integración para dy serán las ecuaciones superior e inferior de las curvas
- Se aplican las ecuaciones de centroide mencionadas arriba
- La integración puede realizarse analíticamente como numéricamente
Entonces el procedimiento mencionado arriba se resume en el siguiente análisis
Solución con Octave
clear
clc
y1 = @(x)x
y2 = @(x)x.^2-20
hold on
fplot(y1)
fplot(y2)
fun = @(x)x^2-x-20
x1 = fsolve(fun,1)
x2 = fsolve(fun,-1)
num = @(x)x*(x-(x.^2-20))
den = @(x)x-(x.^2-20)
cent_x = quad(num,x2,x1)/quad(den,x2,x1)
num2 = @(x)x.^2/2-(x.^2-20).^2/2
cent_y = quad(num2,x2,x1)/quad(den,x2,x1)
plot(cent_x,cent_y,”+r”)
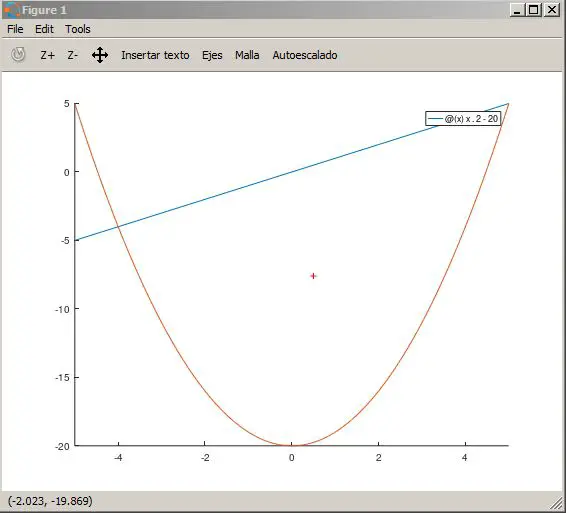
La solución del anterior código devuelve una gráfica como la siguiente, mostrando el centroide como un punto +.
Además, el resultado en la línea de comandos del código debe devolver un resultado parecido al mostrado a continuación:
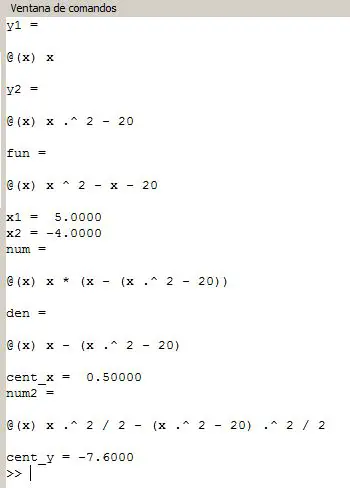
Vídeo explicativo
Para entender el procedimiento de escritura del código arriba, te invito a ver el vídeo en mi canal de youtube:
autor: Marcelo Pardo