Enunciado
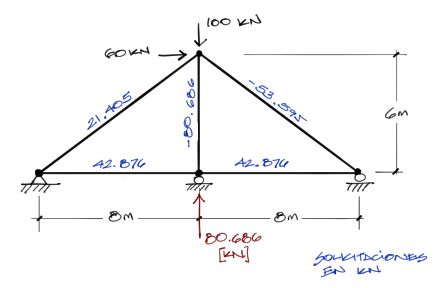
Se pide encontrar las solicitaciones axiales de la cercha hiperestática siguiente:
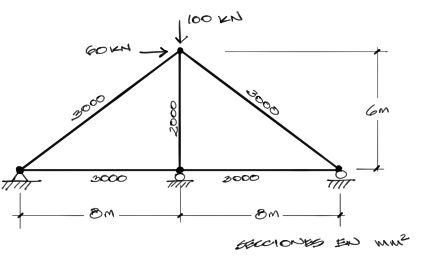
El módulo elástico de los elementos es de E = 200 [GPa]. El método de resolución será por el Principio de Trabajos Virtuales (PTV).
Algo de teoría
Se pueden resolver estructuras de un apoyo redundante (o barra redundante interna) asumiendo cualquiera de las fuerzas redundantes como una carga más. Para esto se debe quitar el apoyo o fuerza redundante para convertir a la estructura en isostática, como se muestra en la siguiente figura:
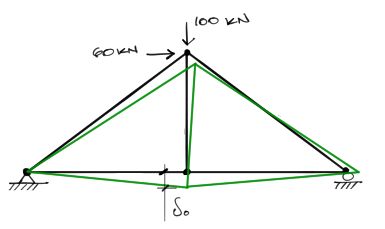
Posteriormente puede resolverse mediante el método de PTV el desplazamiento vertical del nudo del apoyo que se quitó debido a las cargas reales (en este caso la fuerza del apoyo redundante es vertical y por tanto se resuelve el desplazamiento vertical).
A este desplazamiento lo llamaremos δo.
Luego, puede resolverse el desplazamiento vertical δv del nudo de la misma estructura, pero con una carga unitaria en la dirección que se asume tendrá la reacción del apoyo quitado, quitando esta vez las cargas reales.
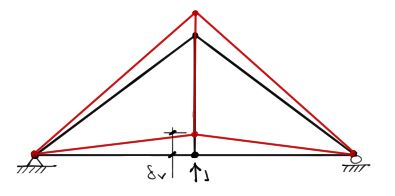
Por el principio de superposición, se puede calcular el desplazamiento total vertical del nudo analizado simplemente sumando las cargas reales más la unitaria, o sumando los desplazamientos de la carga real junto con la unitaria, quedando lo siguiente:
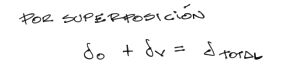
Por el mismo principio de superposición es natural pensar que si actuan la carga unitaria multiplicada por un factor aún desconocido junto con las cargas reales, existe un valor de este factor que logrará que el desplazamiento vertical se anule. Y para conocer el valor de este factor solo es necesario despejarlo:
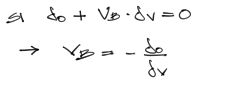
Este valor Vb corresponde a la reacción del apoyo suprimido. Entonces solo queda conocer numéricamente el valor de δo y δv para conocer el valor de Vb. Estos desplazamientos se encuentran con las fórmulas siguientes (obtenidas a partir del PTV):
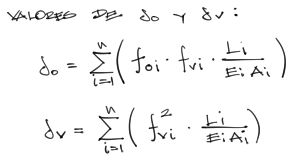
De esta fórmula, las variables que participan son:
- foi: fuerza de la barra i producto de las cargas reales
- fvi: fuerza de la barra i producto de la carga unitaria
- Li: longitud de la barra i
- Ei: Módulo elástico de la barra i
- Ai: Sección transversal de la barra i
Resolución de solicitaciones de las barras por cargas reales
Se plantea entonces la cercha del enunciado quitando el apoyo redundante central (también podía quitarse el apoyo redundante derecho).
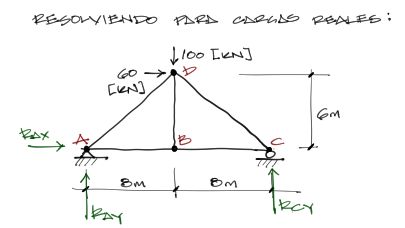
Se resuelven primero las reacciones para la cercha.

Posteriormente se resuelven las solicitaciones de las barras por el métodoo de los nudos. Para el nudo A se tiene
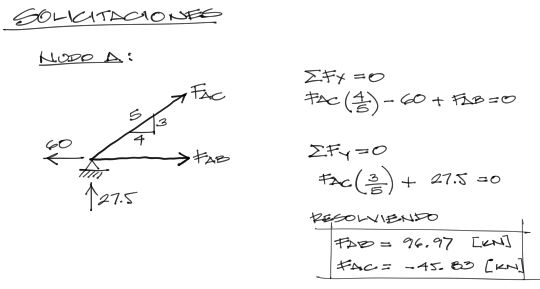
Para el nudo B:
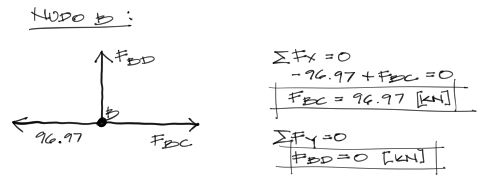
y finalmente para el nudo C. Con esto se tienen las solicitaciones de todas las barras.
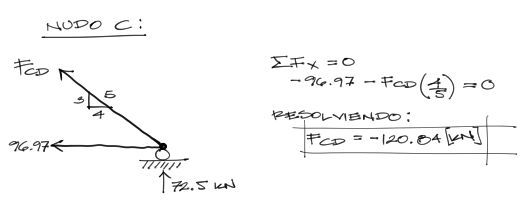
Resumiendo, se muestran todas las solicitaciones de las barras por cargas reales.
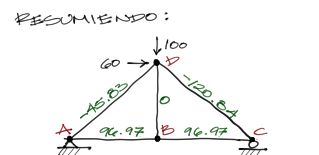
Resolución de solicitaciones de barras por carga unitaria
No se repetirá el proceso para no hacer tediosa la resolución. A continuación se muestra la estructura con la carga unitaria en la dirección de la reacción del apoyo redundante quitado. Luego se resuelven las solicitaciones para esta carga untaria y se tiene:
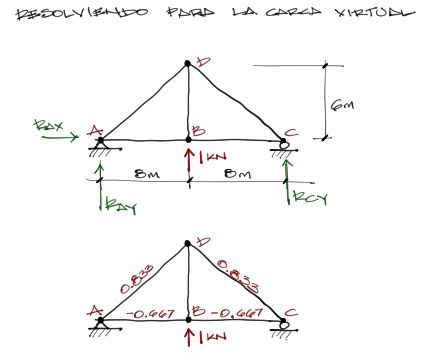
Reacción Redundante Vb
Para encontrar los desplazamientos δo y δv, y a la vez Vb, es conveniente organizar todos los datos necesarios en una tabla, para cada barra. de la siguiente manera. Para cargas reales y para la carga unitaria:
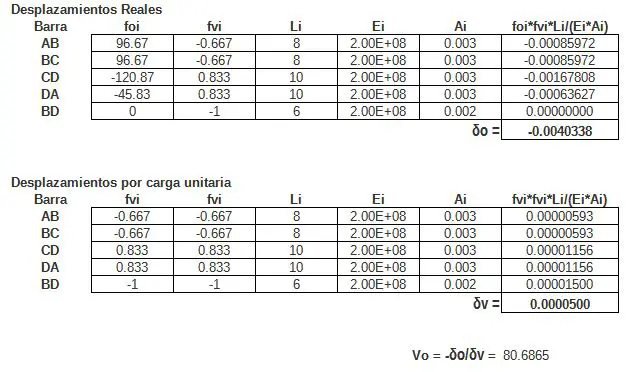
Luego Vb = -δo/δv tiene un valor de 80.686 [KN]. Este se interpreta como el valor de la reacción del apoyo redundante que se quitó primeramente. El signo positivo de Vb indica que la dirección asumida por la carga unitaria es correcta y la reacción del apoyo redundante actúa en esa dirección. Si el signo de Vb es positivo, esto indica que la dirección de la reacción es opuesta a la de la carga unitaria.
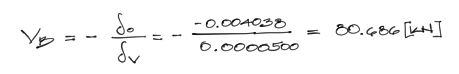
Con base en lo último dicho, la dirección asumida de la carga unitaria no es preponderante. Esto se corregirá con el signo de Vb en caso de que se haya escogido una dirección equivocada.
Resolción de la estructura Hiperestática
Todo el procedimiento mostrado ha servido sólo para determinar el valor de la reacción del apoyo redundante en la cercha hiperestática. Aun no se conocen por tanto las solicitaciones del resto de las barras cuando la cercha contiene el apoyo redundante.
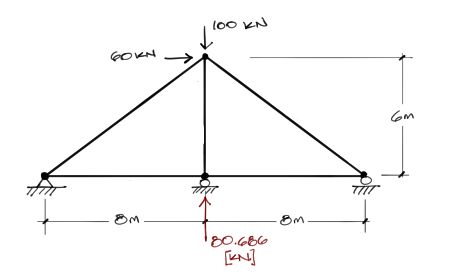
Sin embargo, como ahora conocemos el valor de la reacción redundante, podemos sin ningún problema resolver el resto de las reacciones con las 3 ecuaciones de equilibrio y las solicitaciones de las barras por el método de los nudos o de cortes.
Comprobación con software
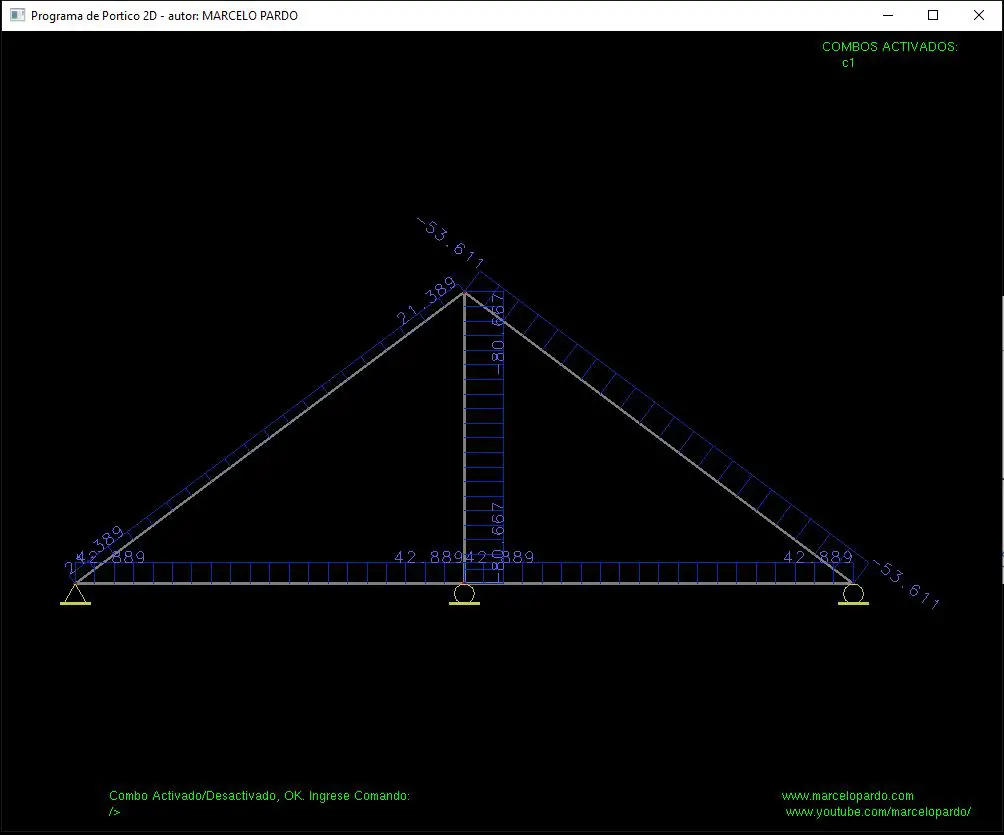
Esta estructura puede comprobarse con un software gratuito que comparto en este enlace: Programa para Pórticos en 2 dimensiones. El archivo de ingreso de datos lo puedes descargar de: Datos de ingreso de Cercha (zip).
Resolución en Vídeo
El ejemplo está resuelto en un vídeo antiguo mio que lo puedes ver a continuación:
autor: Marcelo Pardo


