Introducción

Las zapatas circulares corresponden a una categoría de Fundación Aislada que se utiliza bastante poco, debido a su poca practicidad constructiva como debido a la complejidad en el cálculo de acero y también debido a su dificultad de encofrado, corte y doblado de aceros.

Si embargo contrastando con la complejidad constructiva que presenta, la manera como distribuye los esfuerzos hacia el suelo es una de las más uniformes y simples de calcular entre todos los tipos de formas de fundaciones aisladas que existen.

Bibliografía

La bibliografía sobre el diseño de este tipo de zapatas es limitada, y por lo menos entre los libros que consulté, el único libro que posee información sobre el diseño de acero para este tipo de zapatas es el libro “Cálculo de estructuras de cimentación – J. Calavera”.

Respecto a la forma en la cual la zapata transmite los esfuerzos al suelo, todos los libros de mecánica de suelos o cimentaciones explican este aspecto con total claridad. Tales son los libros de
– Principio de Ingeniería de cmentaciones – Braja Das
– Foundation Analysis and Design – Bowles
– Geotechnical engineering – Murthy
entre otros.

La escasa bibliografía sobre el armado de dichas zapatas nos deja con pocas herramientas para la difusión y dibulgación del diseño de hormigón para dichas zapatas. Sin embargo con criterio adecuado y las herramientas que nos ofrecen los programas computacionales de hoy en día, procuraremos dar una solución acertada a este problema.

Esfuerzos y Asentamiento de la zapata hacia el suelo

Como mencioné antes, existe un contraste muy fuerte en la simplicidad de calculo de los esfuerzos bajo una zapata y la complejidad del cálculo de los esfuerzos dentro de la zapata para calcular su acero.

Según Boussinesq, se puede encontrar el esfuerzo en una masa de suelo a profundidad a partir de una carga de forma circular con la fórmula siguiente:

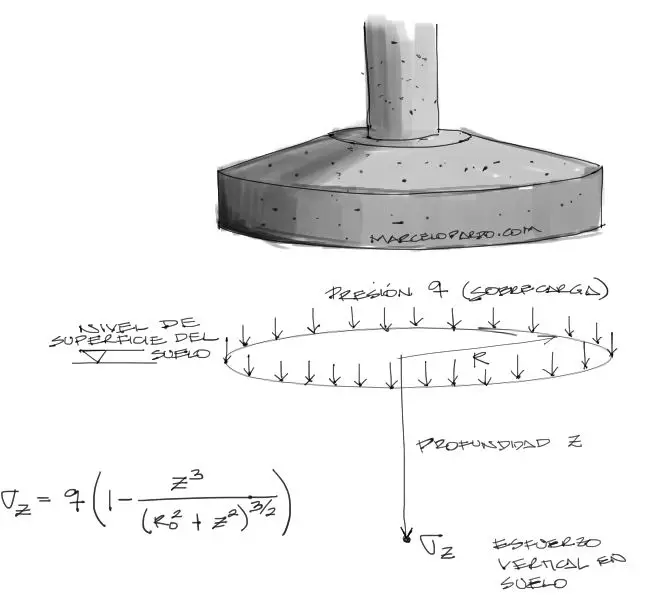
Con la fórmula de esfuerzo vertical producto de la masa de suelo junto con el módulo elástico del suelo o parámetros de consolidación puede encontrarse el asentamiento elástico o de consolidación de la zapata producto de la deformación del suelo. Por el momento no se darán más explicaciones respecto al cálculo de estos asentamientos por tratarse de un tema más extenso del que se hablará en lo posterior.

Capacidad de carga de suelo bajo una zapata circular

Terzaghi ha planteado teorías de falla de suelo a partir de esfuerzos provenientes de zapatas de base circular. Según Terzaghi el suelo con una compacidad alta falla a un esfuerzo de:

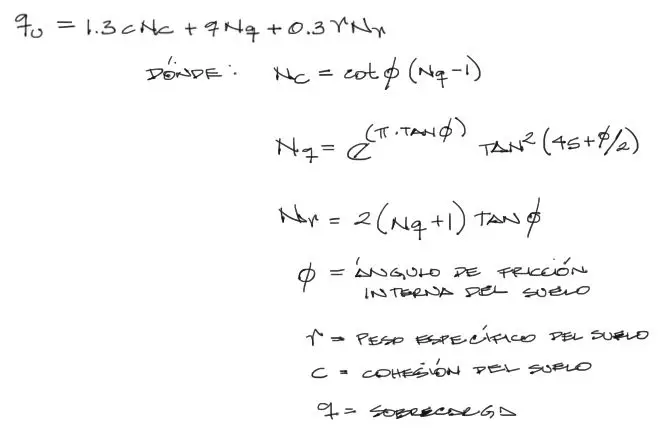
Sin embargo muchos suelos no llegan a una compacidad superior al 70%. Es así que Terzaghi plantea para suelos con baja compacidad, una falla local del suelo a partir de parámetros del suelo factorizados:

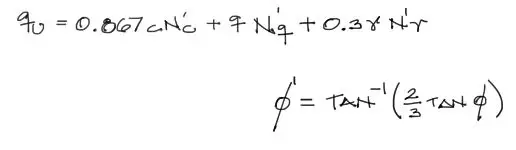
En la fórmula anterior, N’c, N’q y N’ɤ se calculan a partir del ángulo factorizado φ’.

Una vez calculado el esfuerzo al cual el suelo falla, se debe aplicar un factor de seguridad dividiendo “qu” entre 3 o 4 en función al grado de incertidumbre de los datos obtenidos.

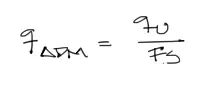
Este esfuerzo admisible se debe comparar con el esfuerzo real aplicado desde la zapata. Si el esfuerzo aplicado es menor al esfuerzo admisible, el suelo no falla. De lo contrario se deberán reducir las cargas o incrementar el tamaño de la base de la fundación.

Diseño del peralte y refuerzo del acero

Refuerzo Radial

El libro de Cálculo de estructuras de cimentación de Calavera indica que se puede reforzar una zapata radial y perimetralmente a partir del equilibrio de bielas y tirantes de una zapata rígida.

El método de bielas y tirantes es una hipótesis de cálculo donde se asume que el hormigón de la cara superior está comprimida transfiriendo los esfuerzos hacia la base mientras se abre, y los aceros inferiores mantienen la zapata “cerrada” impidiendo que se fisure.

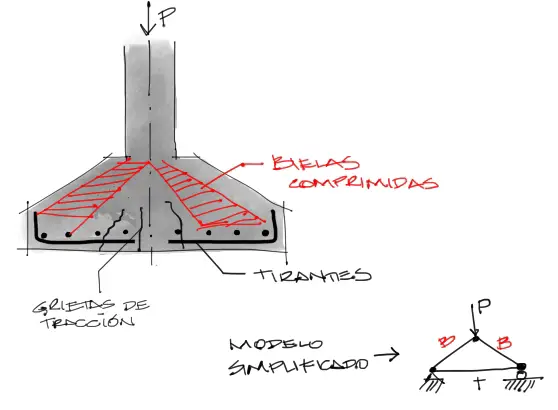
En el equilibrio de los tirantes, los únicos aceros que cumpen una función estructural serían los aceros circulares en una especie de comportamiento de estribo cerrado (como en el caso de estribos de columnas). Los aceros radiales solo cumplen una función constructiva y de armadura de reparto por retracción y fraguado.

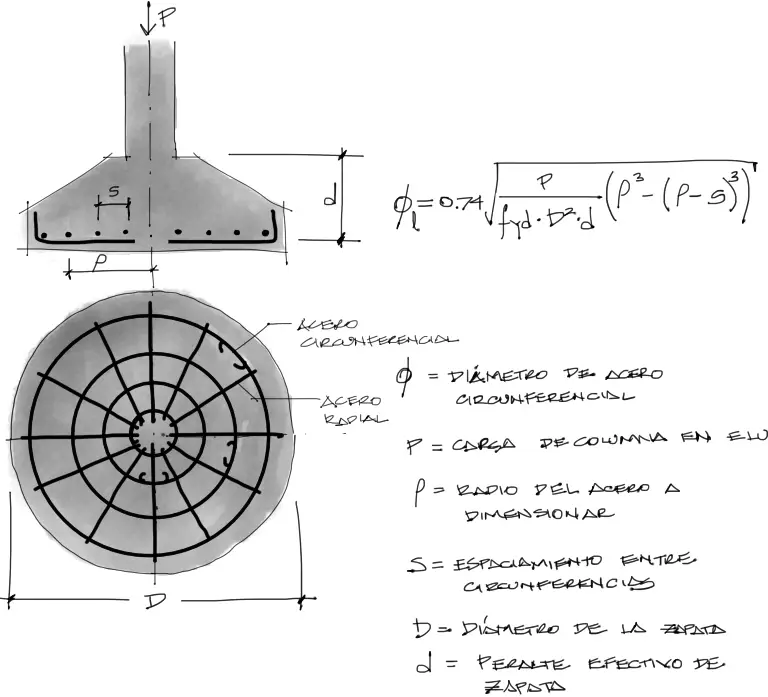
El problema de este cálculo es que para espaciamientos uniformes, el diámetro de cada circunferencia de acero se incrementa a medida que nos alejamos del centro. Esto hace que el armado sea poco práctico.

Por otro lado, el armado radial, debe ser de una quinta parte del acero circunferencial. Calavera sugiere la fórmula:

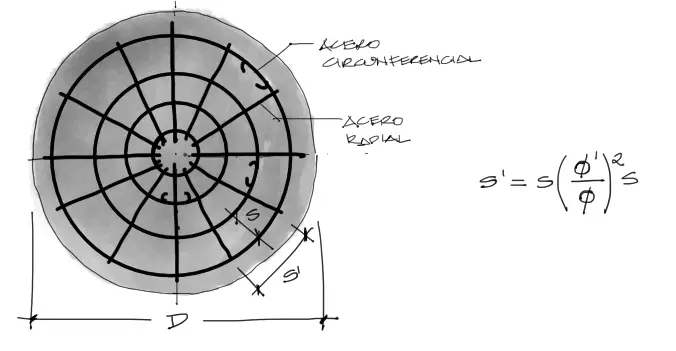
Donde ɸ representa el diámetro de la barra circunferencial y ɸ’ el radial. así mismo s’ corresponde al espaciamiento entre barras radiales. Como el diámetro de las barras se incrementa a medida que nos alejamos del centro, es mejor tomar ɸ como el diámetro de la barra perimetral más gruesa, y s’ corresponderá también a la distancia entre barras en el perímetro de la zapata.

Cabe mencionar que este armado solo sirve para zapatas que cumplen un peralte mínimo que garantice que la zapata es rígida y que puede funcionar bajo la hipótesis de cálculo de biela-tirante. Este peralte mínimo es:

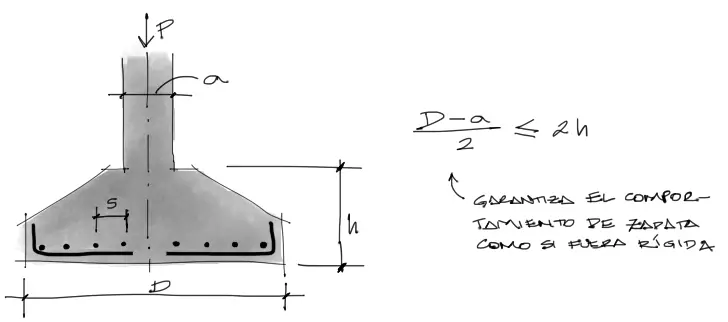
Sin embargo como se mencionó al comienzo, el doblado de las barras, sumado de la variación de diámetros de las barras circunferenciales, más el encofrado circular hacen nada práctico el armado de este tipo de zapatas.

Un aspecto que debo mencionar es que como estos aceros circunferenciales son los únicos que nos resisten la tracción de la base y a la vez cada circunferencia está empalmada en un punto, en cada circunferencia se presenta un punto débil. En este sentido se debe procurar que los empalmes queden en diferentes sectores de la zapata para cada acero circunferencial.

Asimismo, se debe apuntar los ganchos de cada circunferencia de acero hacia arriba, procurando que los ganchos se introduzcan en la zona de compresión del hormigón (zona superior de la zapata) para que funcionen de mejor manera.

Todos estos cuidados a tomar en cuenta hacen poco práctica la construcción de este tipo de armaduras sin equivocaciones por parte del obrero. Esto hace que se prefiera el siguiente tipo de armado, aunque en teoría consiga mayores cuantías de acero que el circunferencial.

Refuerzo de disposición ortogonal

Debido a las dificultades estudiadas en el tipo de refuerzo radial, es más sensato reforzar la zapata a partir de un arreglo rectangular de aceros.

Se puede partir de un análisis de flexión de la zapata en las direcciones ortogonales paralelas a la dirección del acero:

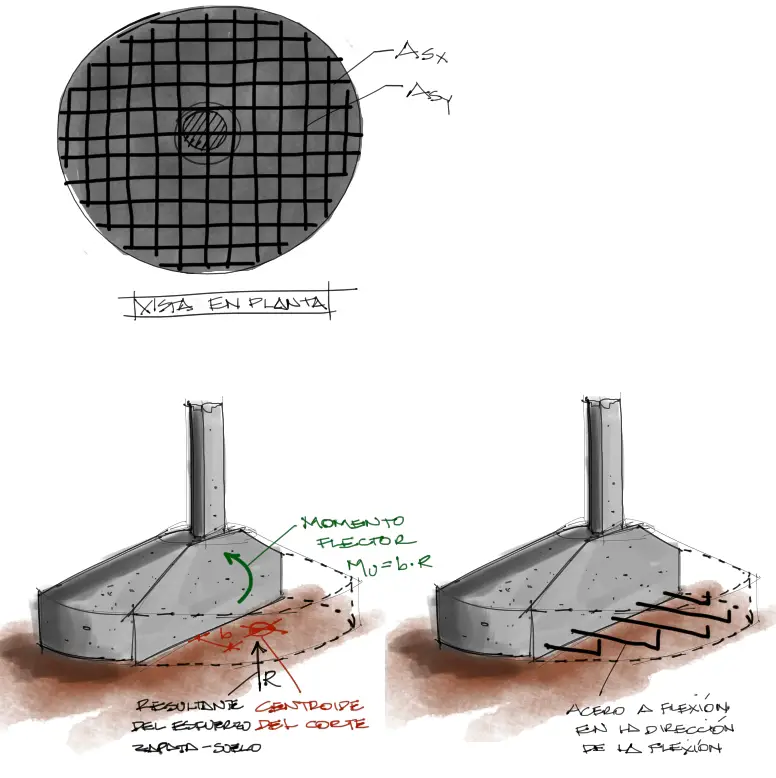
En las direcciones no ortogonales se supone que el momento de flexión Mu es el mismo, por la simetría radial de la zapata. Sin embargo el acero ya no es palalelo o perpendicular al momento flector, dándose el caso más crítico a 45° de las direcciones ortonogales X y Y. En estos casos el refuerzo a flexión que resiste Mu será:

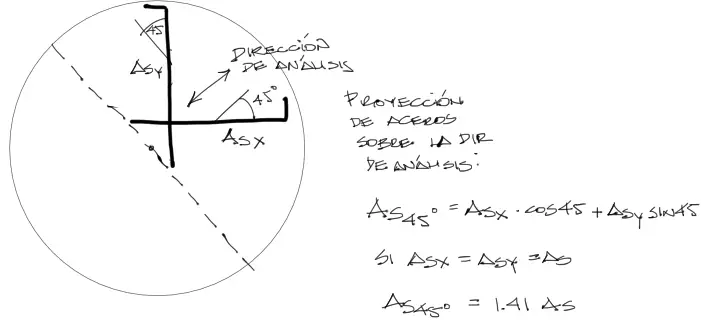
En cualquier caso el refuerzo en dirección de 45° respecto a las direcciones ortogonales será mayor al necesario, sin embargo el exceso de refuerzo compensa la simplicidad del armado.

Verificación a cortante por punzonamiento

Al igual que en zapatas cuadradas o rectangulares, la verificación a cortante por punzonamiento al rededor de la columna es inmediato. Para entender mejor el cálculo por punzonamiento, te recomiendo leer el artículo de DISEÑO DE HORMIGÓN DE ZAPATA CONCÉNTRICA. Si la columna es circular se deben interpretar las variables de la manera siguiente:

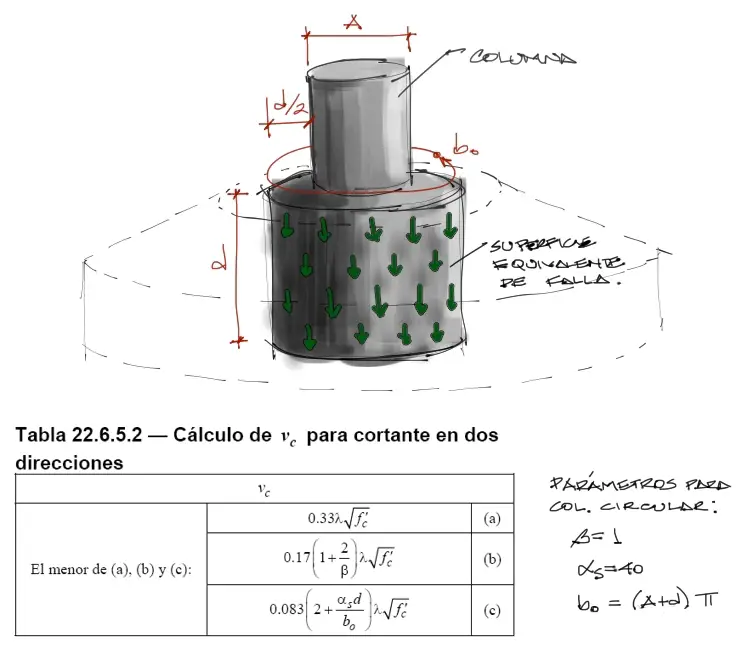
Beta es la relación entre lados largo y corto de una columna cuadrada. En el caso de columnas circulares esta relación será siempre 1. Alfa_s corresponde a la posición de la columna respecto a la zapata. Valdrá 40 para columnas centradas a la zapata, 30 para columna al borde de la zapata, y 20 para columna en esquina de la zapata. bo es el perímetro crítico por donde fallaría por cortante la zapata en caso de que los esfuerzos solicitantes fueran altos. Corresponde al perímetro alejado una distancia d/2 desde la cara de la columna.

Se calculan las tres fórmulas mostradas y la menor de las 3 corresponde a la resistencia del hormigón al punzonamiento. Las unidades de este resultado están en unidades de esfuerzo (KN/m2). Se puede entonces multiplicar vu por la superficie crítica para así obtener la resistencia al punzonamiento en unidades de fuerza y compararla con la solicitación aplicada Pu.

Conclusiones

La aplicabilidad de este tipo de zapatas es limitada. De hecho no hay situación que no pueda salvarse aplicando una columna cuadrada en vez de una circular. Es por tal motivo que en la vida real son pocos los ingenieros que han tenido la oportunidad de ver la construcción de una zapata circular.

Sin embargo, por lo menos para conocimiento general, es bueno tener presente la manera de verificar o calcular los esfuerzos de suelo,capacidad portante y refuerzo de una zapata de esta geometría.

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE HORMIGÓN ARMADO ←←←