Planteamiento del problema

Se desea determinar la deflexión y pendiente de deflexión en el extremo derecho del voladizo. La rigidez constante de la viga es de EI.

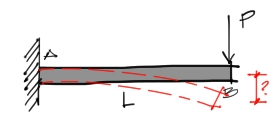
teoría de área de momento

Abordaremos el problema a partir de la teoría de área de momento ya que el caso es adecuado. Como tenemos uno de los extremos inmóvil y complétamente horizontal (en el empotramiento) ya demás el área bajo la curva de momento es sencilla de medir, el método de área de momento es el más apropiado.

La teoría indica que entre dos puntos A y B existe una diferencia de pendiente θAB que es igual al área bajo la curva de momento flector dividido entre la rigidez. A la vez existe una flecha tB/A que es igual al área de momento por el centroide de la figura medida desde el punto B, y todo dividido entre la rigidez.

Resolución de la deflexión y pendiente

Como se mencionó antes, el método de área de momento en este caso es un método rápido y adecuado ya que conocemos que la pendiente en el punto A es igual a cero y forma una línea horizontal de referencia respecto al punto B. Esto simplifica mucho los cálculos y el cálculo de la deflexión en B se resuelve en un solo paso.

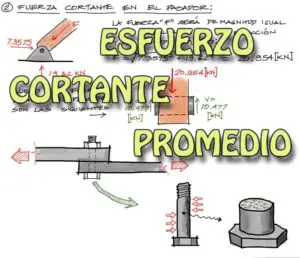
Para resolver el ejercicio primero debemos resolver los diagramas de cortante y momento flector de la viga, que para este caso en particular es bastante sencillo.

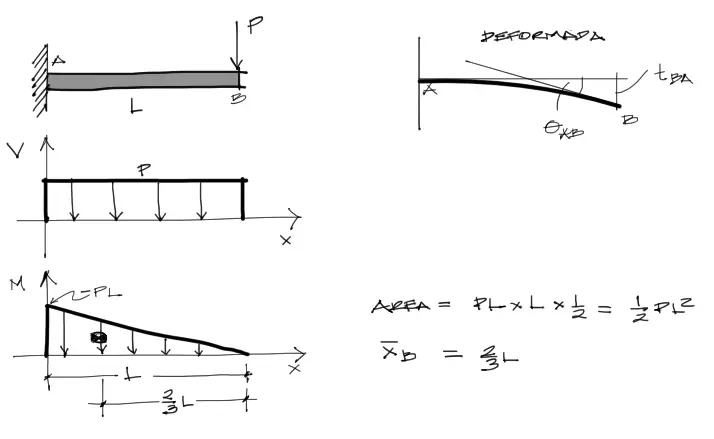
Posteriormente determinamos el área debajo de la curva de momento flector y además el centroide medido desde el punto B de la curva.

Luego la aplicación de la fórmula es inmediata. La pendiente θAB es la misma que la pendiente en B respecto a la horizontal, y la flecha tB/A es la flecha de la viga respecto a la horizontal, por tanto con esto termina el ejercicio:

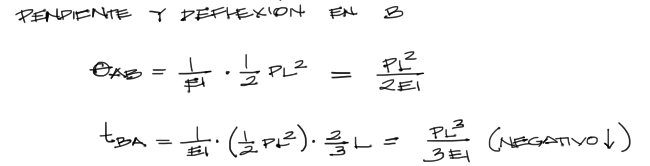
Ecuación de la deflexión a lo largo de la viga

Si se desea encontrar la ecuación de la deflexión a lo largo de toda la viga, debemos aplicar la teoría de la ELÁSTICA DE LA VIGA e integrar 4 veces la ecuación de la elástica donde para este caso en particular la carga distribuida q(x) es igual a cero:

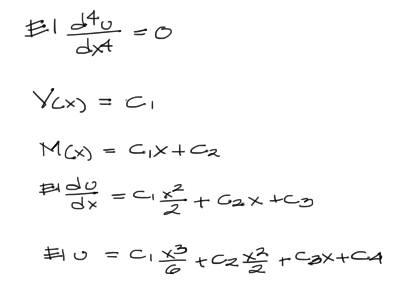
Se generan 4 constantes de integración para lo que necesitamos 4 condiciones de contorno.

Como sabemos cuanto vale el cortante y el Momento flector en X=0, eso nos ayuda para encontrar las dos primeras constantes C1 y C2.

Para conocer las otras dos constantes podemos aplicar condiciones de contorno de deformación. Sabemos que en X=0 la deflexión es igual a cero y también su pendiente, por tanto en X=0: du/dx=0 y u=0. Reemplazando ambas respectivamente en la penúltima y última ecuaciones se consiguen las 4 constantes mostradas en el procedimiento antes de este párrafo.

Finalmente reemplazando todas las constantes C1, C2, C3, C4 encontradas en la última ecuación integrada, se tiene la deflexión en función de la coordenada X para la viga.

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE RESISTENCIA DE MATERIALES ←←←