
¿Qué son las deflexiones?
Las deflexiones son las deformaciones perpendiculares al eje de la viga, responsable de la mayoría de los reclamos de clientes, ya que al deformarse la viga como en la figura, se deforma consigo todo lo apoyado a ellas, como muros de ladrillo o elementos divisorios de vidrio.
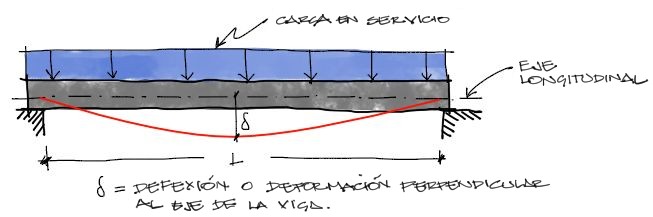
El concepto de deflexión se aplica a elementos de viga y losa para deflexiones verticales producto de cargas gravitacionales, pero también se aplica a columnas para deflexiones producto de cargas laterales de sismo o viento.
Resistencia Vs deformación
Se cree erroneamente que el cálculo estructural es un cálculo sólamente de resistencias de los elementos estructurales. Muchos ingenieros civiles olvidan que algunos de los elementos más crítidos (luces grandes de vigas o losas) deben verificarse también a deflexiones.
Según la mayoría de las normativas el cálculo de resistencias de elementos de hormigón armado se realiza a partir de cargas factorizadas o mayoradas.
En el caso de la Norma ACI 318-25, la mayoración de cargas gravitacionales para el cálculo de resistencias se da a partir de las combinaciones de carga siguientes:
- U = 1.4D
- U = 1.2D + 1.6L
Sin embargo cuando debemos calcular las deflexiones de los elementos estructurales, estos cálculos deben realizarse con las cargas sin factorizar.
- S = 1.0D + 1.0L
¿Para qué se calculan las deformaciones?
Las deflexiones de vigas en estructuras tienen directa relación con la habitabilidad de una estructura. Mientras más se deflecte la estructura, menos segura se sentirá para el usuario final.
Las estructuras deben cumplir con requisitos de seguridad al momento de ser habitados. Estos requisitos están en directa relación con la resistencia de la estructura. Sin embargo también se deben cumplir límites máximos de deformabilidad, y estos están relacionados con las deflexiones de los elementos estructurales.

Un edificio que resista a las cargas de diseño, pero que se deforme mucho, causará una sensación de inestabilidad en el usuario y esto repercutirá en reclamos, susceptibilidades e incluso procesos judiciales hacia la los responsables.
Cálculo de deflexiones en vigas
El cálculo de deflexiones es un tanto complejo y consta de dos partes.
- Deflexiones inmediatas
- Deflexiones diferidas en el tiempo
En este primer artículo abordaremos el cálculo de deformaciones inmediatas.
Cálculo de deflexiones elásticas
Las deformaciones elásticas de una viga se pueden obtener a partir de la teoría clásica de deformaciones de vigas.
Es suficiente con aplicar conceptos de resistencia de materiales clásicos para la obtención de deflexiones:
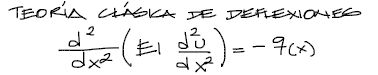
A partir de la ecuación clásica de cálculo de deflexiones se pueden obtener deflexiones de elementos estructurales sencillos o complejos. Para las deflexiones de elementos sencillos existen tablas con las deflexiones al centro del tramo
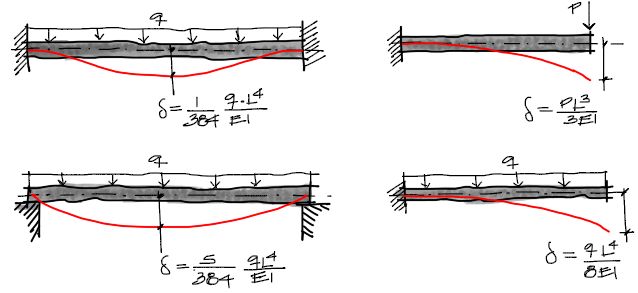
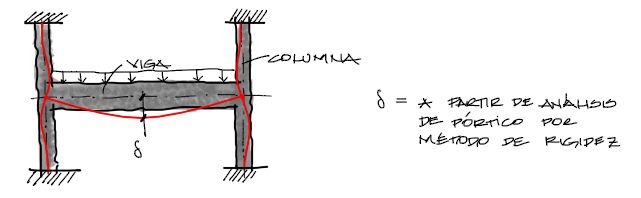
para estructuras más complejas puede aplicarse el método de elementos finitos y así obtener las deflexiones buscadas.



Esta entrada tiene 8 comentarios