Continuación
Para no hacer la resolución muy cargada en una sola página, me tomé la libertad de separarlo en varias partes. Si aún no viste la obtención de la matriz de rigidez del pórtico que ves en la figura, te convendría revisar la PRIMERA PARTE DE RESOLUCIÓN DEL EJERCICIO antes de seguir con esta.
El enunciado es el siguiente:
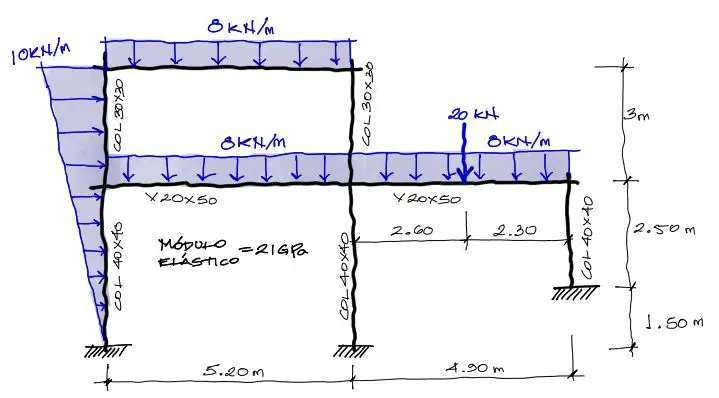
Para el análisis de los desplazamientos de la estructura se necesitan dos cosas. Por un lado la matriz de rigidez, y por otro lado el vector de cargas y fuerzas. Por tanto a continuación nos enfocaremos precisamente en este punto.
Cargas
El siguiente paso para el análisis del pórtico es el encontrar los vectores de carga de esta estructura.
Las cargas se dividen en general en dos tipos: Cargas distribuidas y cargas puntuales. Por comodidad yo le asigno al vector de cargas distribuidas una letra mayúscula {F} y al vector de cargas puntuales la letra {P}
Cargas distribuidas
El caso más general de carga distribuida a manejarse para programar es la carga trapezoidal cargada de extremo a extremo. Si existiera algun caso de viga que solo tuviera mitad de la luz cargada, entonces se debe dividir la viga en dos tramos con nudos en el punto del fin de la carga distribuida.
En nuestro caso de ejemplo, las cargas van de extremo a extremo del nudo, excepto entre los nudos 5 y 9, donde existe una carga puntual. En estos casos igual se debe dividir la viga en dos tramos. Es por eso que se colocó un nudo (7) entre 5 y 9.
Las cargas distribuidas deben transformarse a cargas puntuales equivalentes en los extremos de la viga, según los Momentos de Empotramiento Perfecto. Estos momentos y cargas verticales equivalentes las encuentras en el enlace que acabo de escribir.
Las cargas distribuidas tanto perpendiculares a la viga (en negro) como longitudinales (en rojo) se muestran en la siguiente imagen.
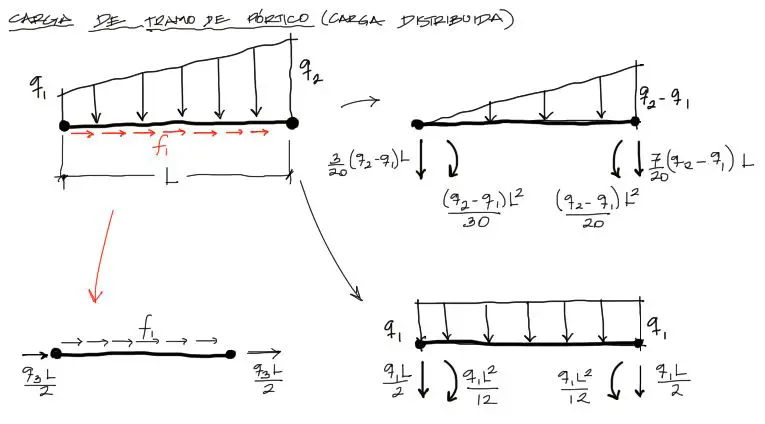
La carga trapezoidal se puede dividir en dos cargas más elementales: la triangular y la rectngular. Si te fijas en las tablas de momentos de empotramiento perfecto del enlace, notarás que tanto para la triangular como para la rectangular ya existen las cargas equivalentes en los extremos del tramo. Si bien en la tabla lo que se muestran son las reacciones en los empotramientos de la viga, para calcular la carga equivalente a la distribuida solo se debe cambiar de signo a las reacciones.
Para la carga longitudinal a la viga simplemente se multiplica la carga distribuida «f» por la longitud de la viga y se divide el resultado entre dos. rara vez existirá una carga longitudinal a la viga no constante en función de x: f(x).
Notarás que aquí tratamos al tramo de análisis como si fuera una viga con el eje longitudinal coincidiendo con la horizontal. Más adelante nos ocuparemos de rotar el elemento para que esté en coordenadas globales.
Una vez encontradas las cargas equivalentes en coordenadas locales de la barra en análisis, el vector de cargas distribuidas {F_local} quedará así:
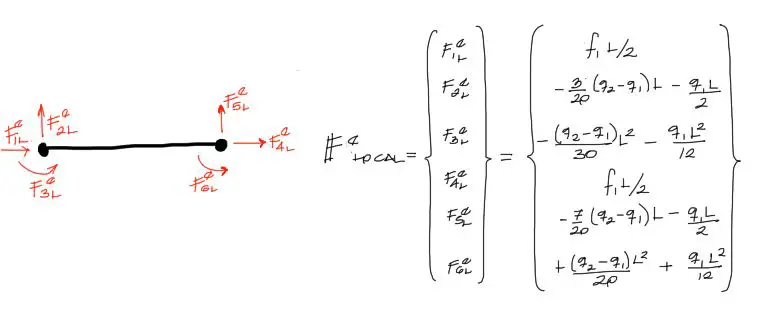
Nota que indico que se trata de coordenadas locales al escribir un superíndice «L» en el nombre del vector, y una «e» indicando que se trata de un solo elemento.
Rotación del vector de cargas distribuidas
La rotación del vector de cargas distribuidas equivalentes {f_local} se logra a partir de la matriz de transformación {T} que se utilizó también en las matrices de rigidez de cada elemento. En las matrices de rigidez se multiplicó {T_trans}x{Klocal}x{T}.
Entonces para la rotación del vector a las coordenadas globales, se aplica {F} = {T}x{F_local}. O lo mismo reemplazando valores:
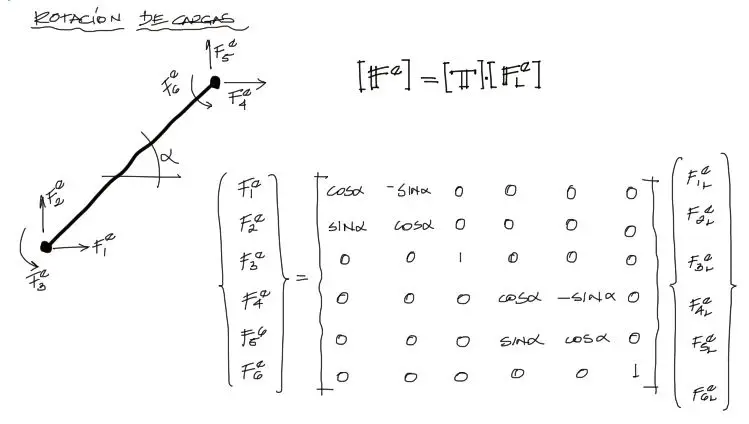
Debemos notar que este vector rotado tiene 6 componentes, que deben tomar la posición de los grados de libertad globales al momento de sumarse con los vectores de los otros elementos. Esto se verá a continuación.
Ejemplo – Cargas de elemento 2
Se escogió de ejemplo el elemento 2 para un cálculo detallado de cargas equivalentes por dos motivos. 1) el elemento está rotado 90 grados (la medición de la rotación del elemento siempre se realiza a partir del eje X positivo en el sentido antihorario). 2) Las cargas son trapezoidales y es el caso más complejo de análisis de carga equivalente. Entonces se tiene el siguiente esquema:
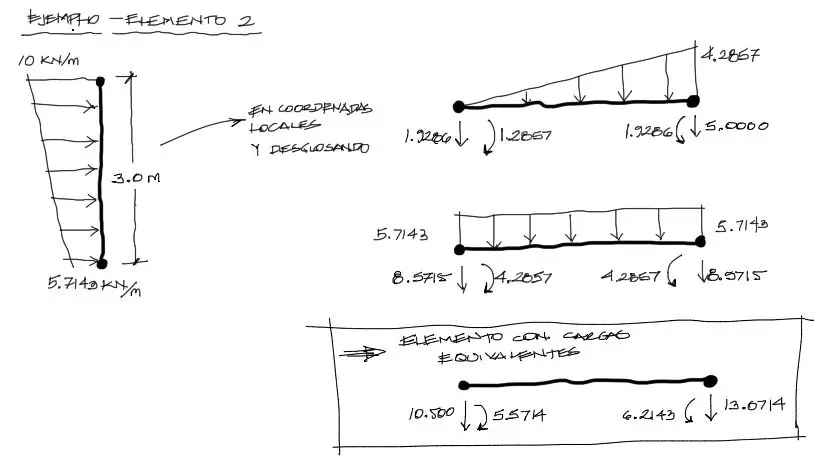
Se divide la carga trapezoidal en rectangular y triangular en coordenadas locales (barra horizontal) para determinar las cargas equivalentes según las fórmulas del anterior apartado. El reemplazo es directo.
Si la carga trapezoidal estuviera en el otro sentido (q1 mayor a q2) simplemente habría que invertir los valores de la carga triangular. Este sin embargo no es el caso.
Luego se suman los aportes de la carga triangular y rectangular para conformar el vector de cargas equivalentes en coordenadas locales. Se tiene entonces:
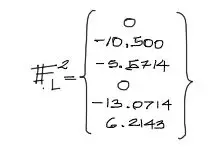
Este vector se debe rotar a partir de la matriz de transformación para un ángulo de 90°. Se procede a la rotación:

Notemos que el vector F2 ya no lleva el subíndice «local» luego de la rotación. Por otro lado se anotaron en rojo los índices de la posición que tomará cada uno de estos valores del vector cuando se traslade al vector de fuerzas con los 27 grados de libertad en columna.
Ejemplo – Cargas de elemento 7
Para este elemento el procedimiento es similar aunque más sencillo, pues no existe carga trapezoidal y además que la rotación de este elemento es de cero grados. Se procede al cálculo de cargas equivalentes a partir de los momentos de empotramiento perfecto entonces.
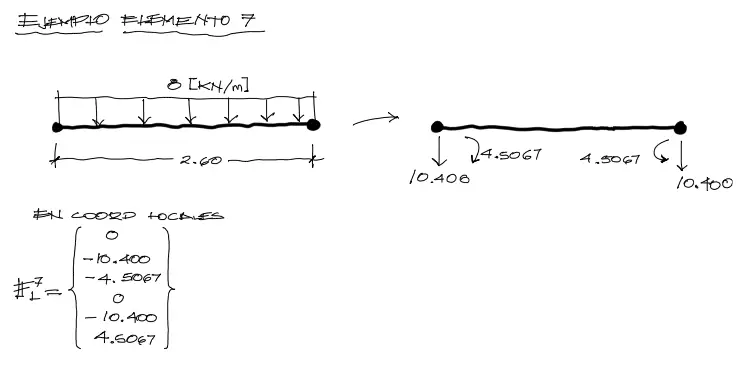
Una vez calculadas las cargas equivalentes y trasladadas al vector de fuerzas locales se realiza el cómputo de la rotación (a pesar de que en este caso no exista la rotación, se procesa la multiplicación para mostrar que el procedimiento mecánico se debe repetir para todos los elementos). Obviamente el vector Global es igual al local en este caso.
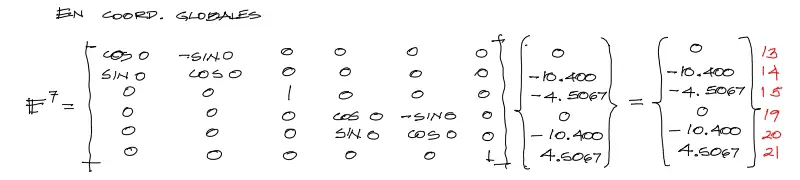
Se deben notar dos aspectos en este vector encontrado. Primero, el vector de fuerzas equivalentes no incluye la carga puntual de 20 KN aplicada en el nudo derecho del elemento. Las cargas puntuales aplicadas en la estructura se deben cargar en otro vector de cargas puntuales que mostraremos más adelante.
El segundo punto a destacar es que en este caso los índices en rojo no son correlativos, sino que saltan del 15 al 19. Esto sucede también en la matriz de rigidez del elemento 7 y se debe al salto en la numeración de los nudos. AL momento de trasladar estos valores al vector de cargas equivalentes con los 27 grados de libertad, los 6 valores se separarán en dos partes para tomar su posición global.
Suma de aportes de cargas equivalentes {F}
Una vez obtenidas las cargas equivalentes de todos los elementos, se deben sumar. Para esto, cada elemento debe tomar las posiciones de los índices rojos mostrados arriba, en un vector de 27 posiciones (correspondiente a los 27 grados de libertad del ejercicio). Luego se suman todos.

Cargas puntuales {P}
La generación del vector de cargas puntuales es más sencillo. Se debe simplemente armar un vector {P} vacío de 27 filas e ir transportando dentro todas las cargas puntuales en el grado de libertad correspondiente. En este caso la única carga puntual es de 20KN apuntando en la dirección negativa en Y, por tanto los -20KN se cargan en el grado de libertad 20 (coincidencia).
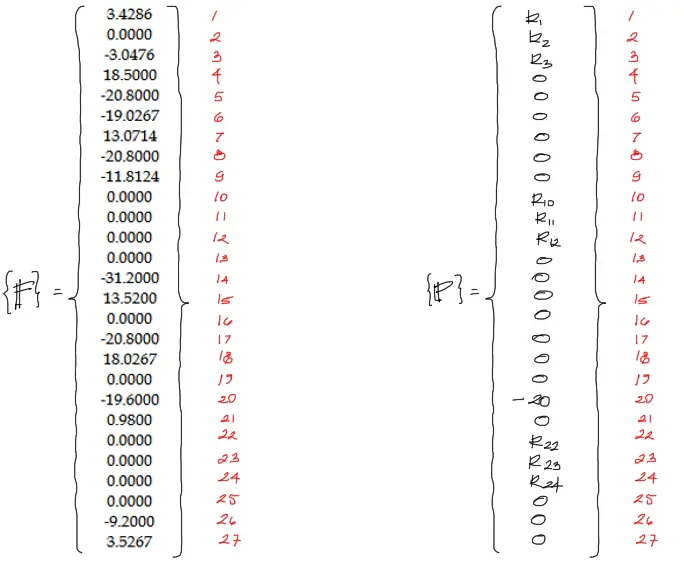
Además de las cargas puntuales, nota que se anotan en este vector las reacciones producto de los grados de libertad restringidos. en este caso por tratarse de empotramientos, los tres restringidos de cada nudo de la base tienen desplazamiento cero, y por tanto, en estos grados de libertad aparecen reacciones Ri.
Código de ensamblaje en Octave (Matlab) y vídeo tutorial
En la publicación del enlace puedes ver un vídeo tutorial donde enseño como ensamblar el vector de fuerzas distribuidas de manera automática en Octave o Matlab. Además puedes descargar el código *.m
ENSAMBLAJE DEL VECTOR DE CARGAS DISTRIBUIDAS POR OCTAVE/MATLAB 
Qué sigue?
A continuación se resuelve el sistema de ecuaciones para encontrar los desplazamientos del sistema. Esto se realizará en el siguiente enlace, para no extender esta explicación en una sola página.
autor: Marcelo Pardo
→→→3ra PARTE: SISTEMA DE ECUACIONES Y CÁLCULO DE DESPLAZAMIENTOS →→→