Enunciado
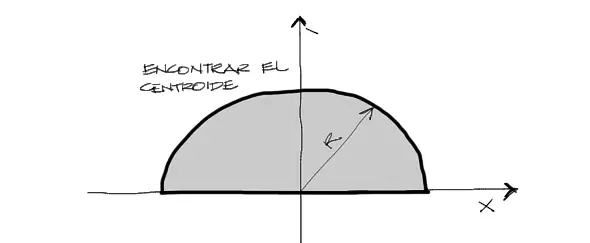
Encontrar el centroide del semicírculo mostrado en la imagen siguiente:
Resolución
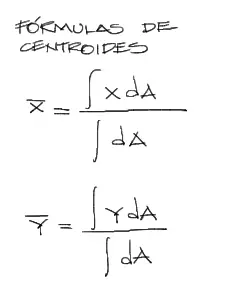
Fórmulas de centroide
Referenciando la pieza según ejes coordenados cartesianos, el centroide de la pieza se expresa a partir de las siguientes dos fórmulas:
Sin embargo si queremos integrar el diferencial de área a partir de coordenadas cartesianas el trabajo de integración se complica bastante. Es en este sentido que es mejor aplicar la transformación de coordenadas cartesianas a coordenadas polares para el trabajo diferencial e integral. Entonces el elemento diferencial de área que podría bien ser dx·dy es preferible concebirlo a partir de arcos y radios:
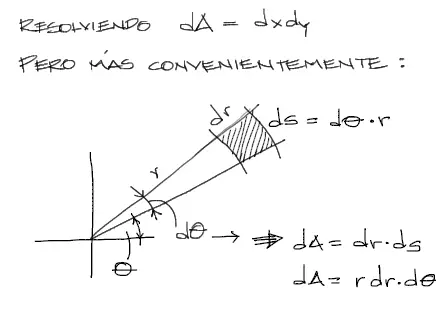
Se debe tomar el cuenta en este procedimiento que el diferencial de arco ds es para ángulos pequeños igual al radio multiplicado por el diferencial de ángulo.
Diferencial de área
Una expresión común a ambas fórmulas de centroyde en X y en Y es el denominador de ambas fórmulas: la integral del área. Es por eso que primeramente integraremos esta integral. El diferencial de área es igual a r·dr·dθ. por tanto la integración es inmediata, tomando en cuenta los límitas para el radio desde cero hasta R y para el ángulo desde cero hasta π.
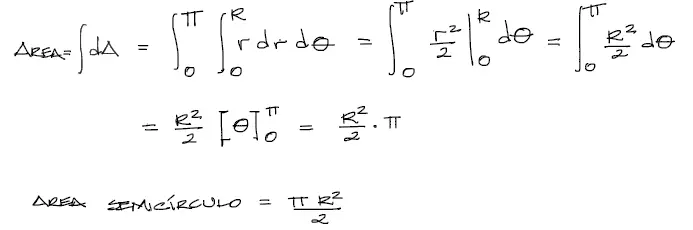
Centroide en X
Para resolver el numerador debemos previamente convertir el término dentro de la integral “x” en su equivalente polar a partir de radios y ángulos. Se tiene entonces:
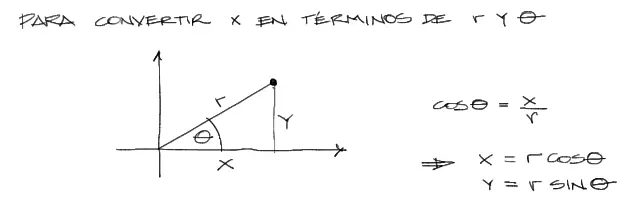
Luego reemplazando esta conversión en la ecuación ʃxdA y luego integrando, se tiene:
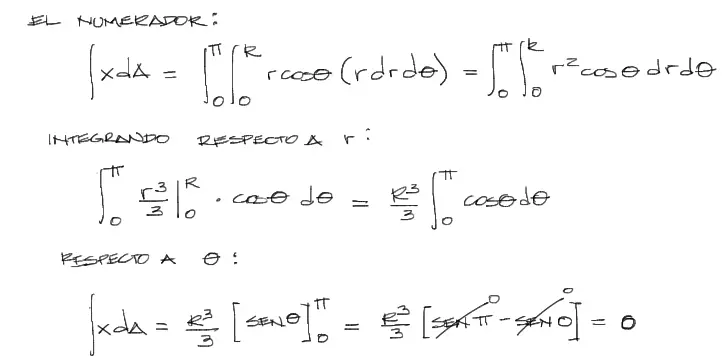
Y finalmente reemplazando tanto numerador como denominador en la fórmula de centroide en X
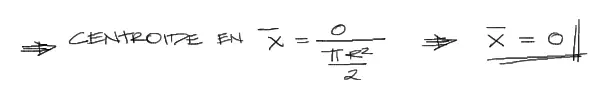
Centroide en Y
Se repite el proceso para el numerador de centroide en Y, tomando en cuenta que y = r·sinθ. Entonces reemplazando todas las variables en coordenadas polares:
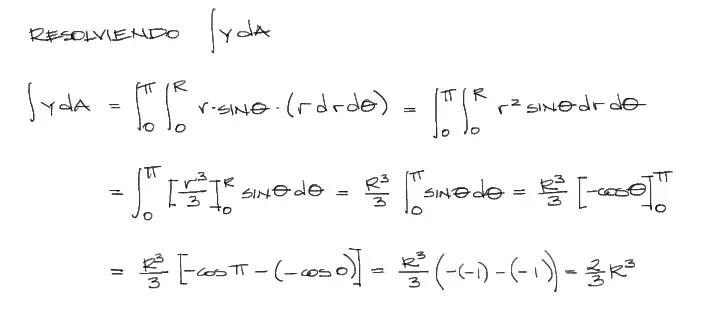
Ahora con el numerador y el denominador reemplazados en la fórmula del centroide en Y:
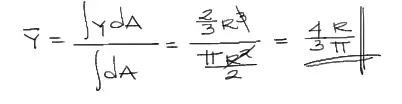
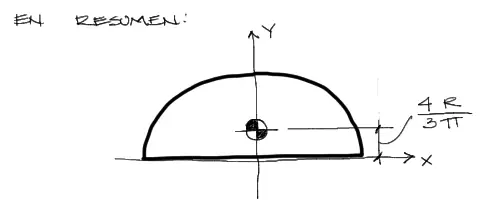
Graficando
La posición gráfica del centroide de la pieza es
autor: Marcelo Pardo
←←← VOLVER A TABLA DE CONTENIDO DE ANÁLISIS ESTRUCTURAL←←←
←←← VOLVER A TABLA DE CONTENIDO DE RESISTENCIA DE MATERIALES ←←←