Enunciado

Encontrar la deflexión de la viga mostrada a continuación sometida a carga distribuda:

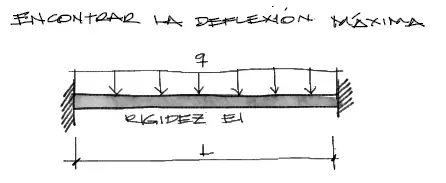
Resolución

Método de la elástica

Se aplicará la resolución por el método de la elástica, integrando la ecuación diferencial de la viga:

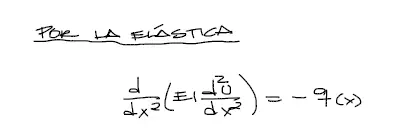
Como la inercia EI es constante y la carga también, se puede simplificar la ecuación como:

Luego integramos cuatro veces hasta obtener la deflexión de la viga u sin derivar respecto de X

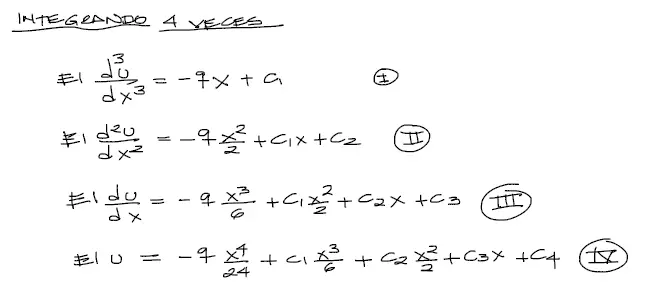
Se generaron 4 constantes de integración que se deben averiguar

Condiciones de contorno

Tanto al arranque (x=0) como al final de la viga (x=L) la deflexión o desplazamiento vertical de la viga es nulo, por tanto u=0. De la misma manera en los mismos puntos, por el empotramiento, el giro de la viga es cero, y en esencia du/dx=0. Entonces:

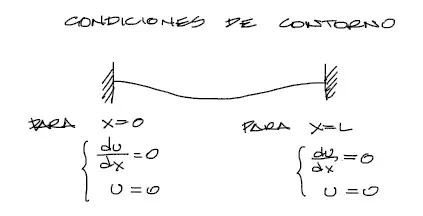
Constantes de integración

Son 4 constantes de integración por resolver y además se tienen 4 condiciones de contorno por lo que el problema está completamente definido. Se reemplaza x=0 y u=0 en la cuarta ecuación intgrada y x=0 con du/dx=0 en la tercera. Se procede de la misma manera para las condiciones de contorno en x=L.

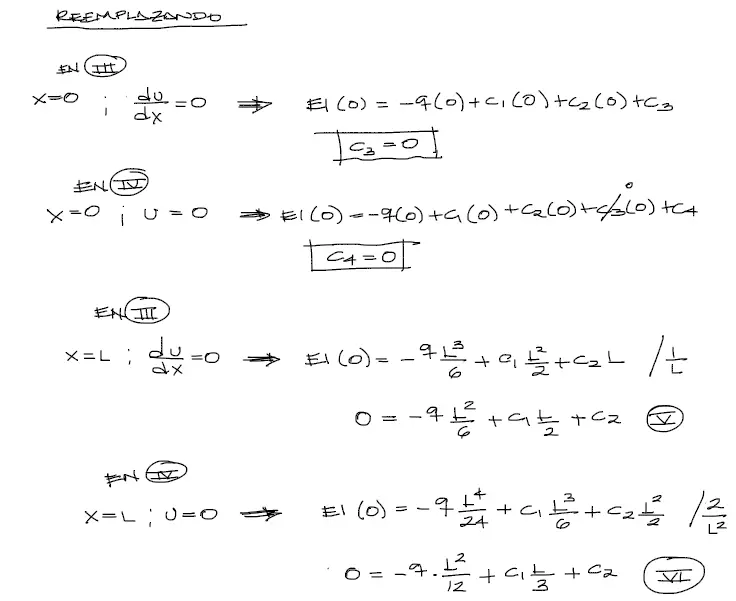
De los reemplazos en x=L obtenemos dos ecuaciones con dos incógnitas. Restamos ambas ecuaciones

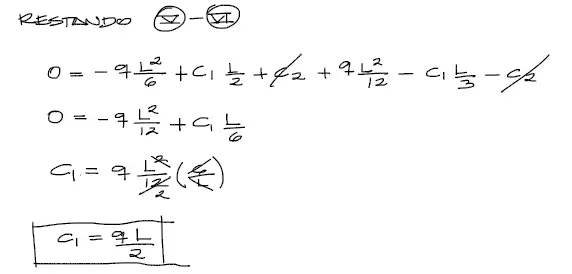
Obtenido C1, reemplazamos este valor en la ecuación (V)

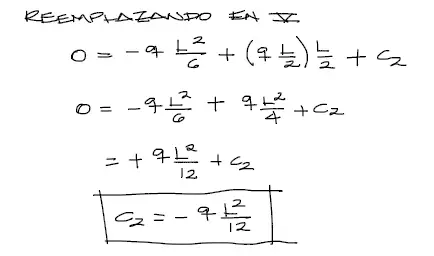
La ecuación de la elástica de la viga

Con las 4 constantes encontradas se puede volver a escribir la ecuación de la elástica integrada para cualquier punto de la viga «x»

Luego, reemplazamos dentro de la elástica el punto de deflexión máxima x=L/2 dentro de la ecuación de la elástica en función de x:

gráficamente se tiene:

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE RESISTENCIA DE MATERIALES ←←←