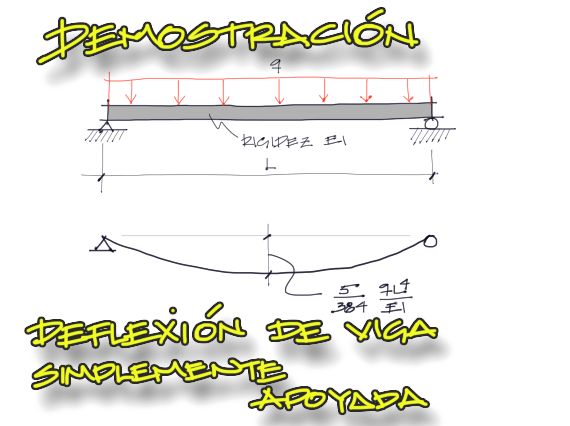
Demostración de ecuación de deflexión de viga simplemente apoyada

Enunciado

Se debe encontrar la deflexión de la viga simplemente apoyada con carga distribuida, con los datos de longitud y rigidez mostrados.

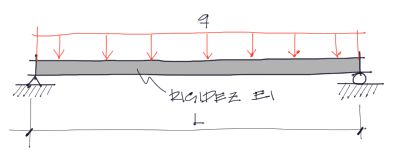
Demostración

Se comienza por la definición de la ecuación de la elástica de la viga para una carga distribuida constante:

Al integrar 4 veces, se generan 4 constantes de integración. Éstas se resuelven con 4 condiciones de contorno:

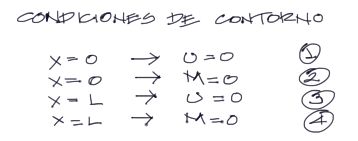
Se reemplazan estas 4 condiciones en las ecuaciones de momento flector (segunda derivada de U) y deflexión de la viga.

La constante C3 está en función de C1 que ya fue encontrada. Se realiza el reemplazo de C1 en la condición de contorno 3 y se tiene:

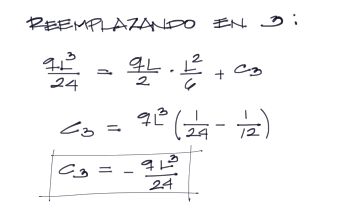
Finalmente reemplazando las cuatro constantes en las ecuaciones de la elástica, se tiene toda la información de la viga. Recordemos que la tercera derivada de la deflexión representa el cortante, la segunda derivada representa el momento flector, la primera derivada indica la pendiente de la viga en función de (x) y la última ecuación representa la deflexión de la viga multiplicada por la rigidez EI.

Si queremos encontrar la deflexión al centro de la viga, reemplazamos x = L/2, y operando:

Notar que la deflexión U debe despejarse de la rigidez. El resultado es ya el conocido valor de 5/384*q*L^4/EI de la bibliografía. El signo negativo indica que la deflexión se dirige hacia abajo en el eje de las “Y”.