
Planteamiento
Las fórmulas del método de pendiente deflexión puede que te resulten conocidas y son las que se muestran a continuación:
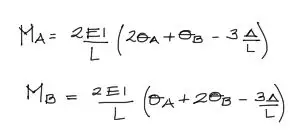
Desarrollo
Para llegar a estas fórmulas, asumiremos un elemento de viga empotrada en sus dos extremos y con una longitud L, Además esta viga tiene rigidez EI.
A esta viga le imponemos giros en ambos extremos, y además un desplazamiento del extremo derecho, como se muestra en la figura.
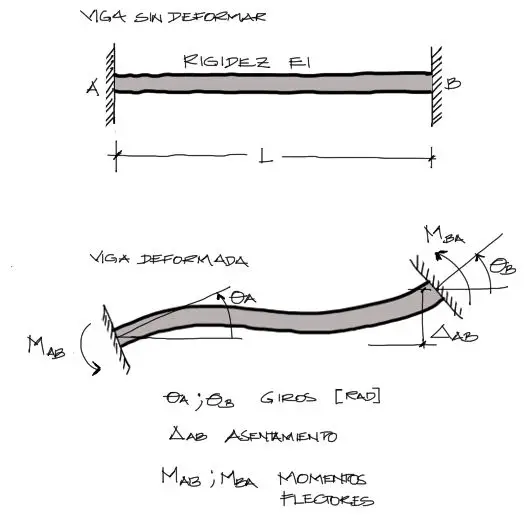
Se desea entonces encontrar la relación que existe entre estos giros y desplazamiento impuesto, y los momentos flectores en los extremos producto de estos giros. Los momentos en los extremos los llamaremos Ma y Mb, tal cual se muestra en la imagen arriba.
Estrategia
Para resolver esta viga emplearemos la teoría de la elástica de la viga, donde para este caso particular la carga distribuida es cero, por tanto, se tiene:
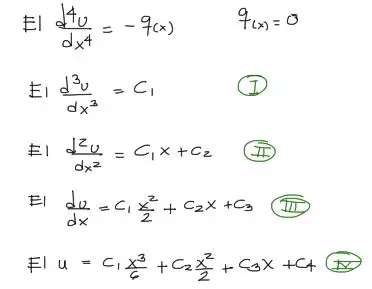
De la ecuación de la elástica, se hizo la integración respectiva 4 veces, y las ecuaciones formadas son las mostradas arriba. Para resolver el problema se necesitan además 4 condiciones de contorno y así resolver las cuatro incógnitas generadas C1, C2, C3, C4.
Las condiciones de contorno son: en el extremo izquierdo, x=0, se tiene deflexión u = 0 y pendiente du/dx = GiroA. En el extremo derecho x = L se tiene una deflexión u = DeltaAB y un giro du/dx = GiroB. Eso se muestra en la siguiente figura:
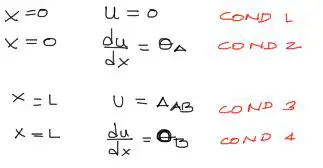
Resolución de las constantes de integración
Con el reemplazo de las condiciones de contorno del extremo izquierdo, en x=0, se encuentran las constantes C3 y C4 inmediatamente, reemplazando u y du/dx en las ecuaciones de la elástica III y IV:

Las otras dos condiciones de contorno en x=L se reemplazan nuevamente en las ecuaciones III y IV de la elástica, y se obtiene el siguiente sistema de dos ecuaciones con dos incógnitas (C1 y C2).

Se resuelve C1 del sistema tras unas cuantas operaciones.
Para encontrar C2, se reemplaza C1 en la ecuación VI y se tiene:
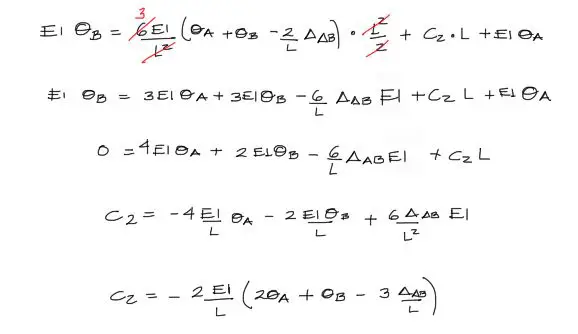
Ecuación general de momento en función de X
Reemplazando C1 y C2 en la ecuación de la elástica II, se obtiene el momento flector en función de x:
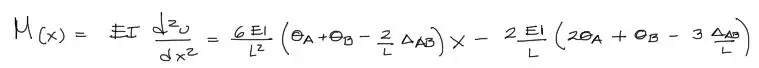
De esta ecuación, para conocer el momento en el extremo izquierdo Ma, se puede reemplazar x = 0. Para Mb del extremo derecho se reemplaza X = L. Se tiene finalmente:

Como ves, hemos encontrado ya la respuesta buscada, con una leve discrepacia de signos. Esta discrepancia de signos en el Ma se debe a que el momento encontrado corresponde al diagrama de momentos. Si transformamos este momento negativo a la convención de signos de las ecuaciones de equilibrio, tenemos:
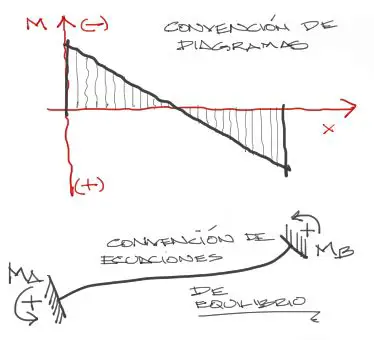
y finalmente entonces se tiene:
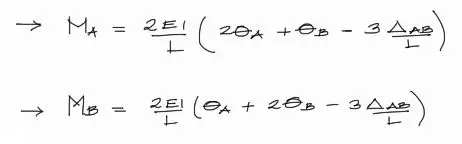
Para completar las ecuaciones se debe incluir a las ecuaciones de momento Ma Y Mb, los aportes de momento de empotramiento perfecto por parte de las cargas en el tramo. Estos momentos de empotramiento perfecto MEP los sumamos a cada ecuación de momento y queda:
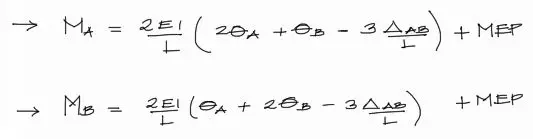
autor: Marcelo Pardo
← ← ← VOLVER A TABLA DE CONTENIDO DE ANÁLISIS ESTRUCTURAL← ← ←
Hola, muchas gracias por tu enseñanza.
Una pregunta: Cuando estudié este método, aprendí a utilizar:
(3EI/L)(@N-Phi)+Me
Donde (por razones del teclado dela teléfono no puedo detallar bien la ecuación):
EI: Rigidez
@N: Teta del Nodo cercano (Rotación del Nodo Cercano)
Phi: 3Delta/L (Desplazamiento de un apoyo)
Me: Momentos de Empotramiento Perfecto
Continuando con la duda, usaba esa ecuación cuando en un tramo de la viga sólo uno de sus extremos estaba empotrado, esto a la vez conllevaba que yendo en dirección del extremo “no empotrado” al que si lo estaba el Mij fuera “cero” o mejor dicho esa ecuación era nula. Algo que también afectaba y/o cambiaba era que los momentos de Empotramiento para ese tramo se calculaban como tal (extremo empotrado y el otro no) que a su vez por estar uno de sus extremos no empotrados ese momento era “cero”.
Espero haberme explicado y lo que deseo que me aclares es la forma o por qué puede llegarse a las mismas respuestas de esta manera, como influyen esos pequeños cambios, lo que me puedas explicar acerca de esto será aceptado de la mejor manera.
Muchas gracias de antemano y éxitoen todo.