Introducción

Se analizó en una publicación anterior Introducción a diagramas e interacción cuál es la manera de obtener diagramas de interacción de la resistencia de un material para piezas de sección homogenea. Esa publicación servirá de muy buena base para realizar la demosatración de las fórmulas del diagrama de interacción de una columna de hormigón armado

Una de las principales diferencias entre este diagrama de interacción con los diagramas de materiales homogeneos es que en hormigón armado se trabaja con la sección fisurada. Esta diferencia se debe a que se debe aprovechar la máxima resistencia del hormigón y del acero (estado límite último). Sin embargo al trabajar tan cerca de los límites de rotura de los materiales estos sufren altas deformaciones y estas deformaciones fisuran al hormigón.

Demostración de las fórmulas

partimos de una sección de hormigón como la mostrada a continuación, donde las dimensiones de la sección, h, b, d, d’, y las cantidades de acero As y As’ son conocidas:

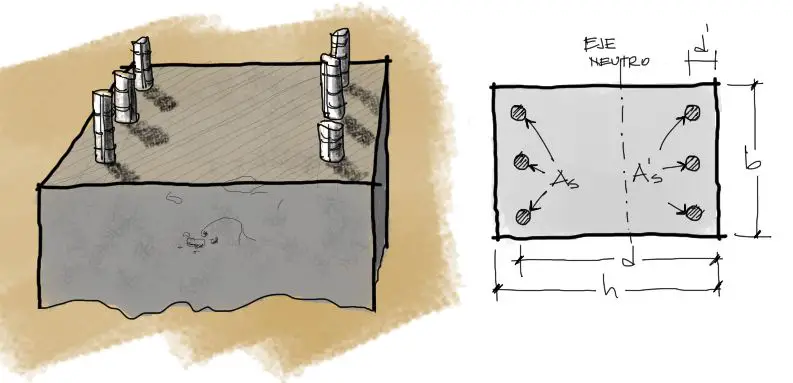
Por simplicidad se analizará una sección de hormigón con solamente aceros en las posiciones mostradas. Más adelante se hará el análisis para más filas de acero en las caras laterales perpendiculares al eje neutro. El acero As se refiere al acero que en situación de Momento flector puro estaría opuesto a las fibras de compresión. As’ corresponde al acero que en caso de flexión pura estaría comprimido junto con el bloque de compresión de hormigón.

En la anterior publicación apliqué una fuerza axial que generaba esfuerzos de compresión internamente a la sección e hice lo mismo para un momento de fuerza. Posteriormente realicé la combinación de ambos efectos y analicé los esfuerzos internos que se generan. Posteriormente hice una parametrización de las solicitaciones en función a una variable de excentricidad “e”.

Se hará un análisis similar aquí. Para eso partimos de los siguientes esfuerzos y fuerzas internas en la sección de la columna aplicadas en el centro de la sección:

Se debe hacer un breve análisis de los esfuerzos internos en esta sección. Para empezar, el motivo por el cual solo una fracción de la columna se encuentra en compresión es porque el análisis ya se lleva a cabo en una sección agrietada. Por otro lado la fuerza de tracción y la fuerza de compresión en el acero marcadas ambas en amarillo se debe a fuerzas del acero llevadas al límite de fluencia. Para entender mejor los conceptos de sección agrietada te recomiendo leer el artículo de Cuantía balanceada y ver el vídeo correspondiente al final de ese texto.

En el manejo de variables, el subíndice “n” de Pn y Mn se refiere a “nominal”, que en otras palabras se refiere a la carga máxima que puede resistir el material (equivalente al Padm y Madm del artículo anterior).

Equilibrio de fuerzas

La fuerza interna de compresión “Pn” en la sección debe equilibrarse con los esfuerzos internos dentro de los materiales multiplicados por la sección donde se aplican. En el caso de la sección de acero tanto a tracción como a compresión, el esfuerzo del acero “fs” y “fs'” se aplica sobre la sección transversal de los aceros As y As’ respectivamente. Nota que a diferencia de vigas de HoAo, el esfuerzo del acero no necesariamente llega a la fluencia “fy”. Esto dependerá de las deformaciones generadas en la columna en base a la posición de Pn y de la magnitud de “e”. Veremos más adelante este concepto.

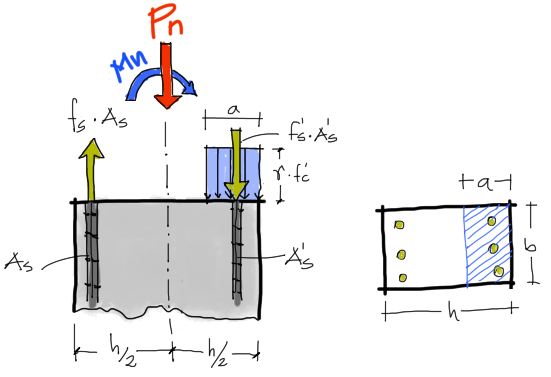
En el caso del hormigón, el esfuerzo generado por la compresión es ɤ·fc’ donde ɤ=0.85. Este esfuerzo es aplicado en una superficie a·b como se ve en el gráfico. Resumiendo, la fuerza interna Pn genera fuerzas equivalentes en la sección iguales a:

En esta ecuación no entra el momento resistente Mn, pues se trata de un momento flector y no una fuerza

Equilibrio de Momentos

Al igual que con fuerzas, el momento flector interno resistente Mn se puede escribir como la equivalencia de fuerzas del hormigón y acero producto de los esfuerzos internos generados. Si tomamos como pivote el centro de la columna, las fuerzas excéntricas al centro generan brazos y a la vez momentos de fuerza. Al equilibrar estos momentos de fuerza se tiene:

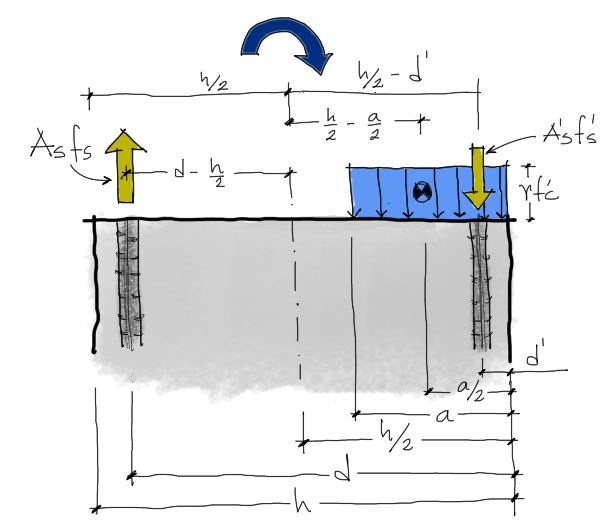
Recuerda que el pivote es el centro de la columna. Entonces:

Diagrama de compatibilidad de deformaciones

Habia mencionado arriba que debido a la naturaleza de los esfuerzos de columnas, los aceros a tracción y compresión pueden no fluir al momento en que el hormigón falla. Por ejemplo, se pueden dar las siguientes situaciones de deformación de la viga al momento de la falla del hormigón:

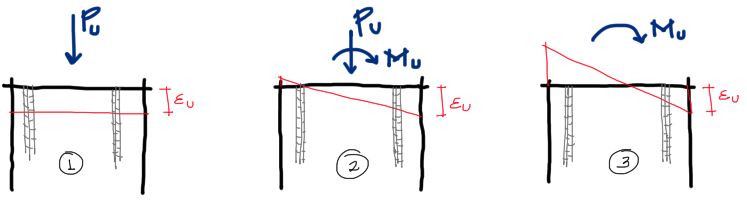
Las líneas rojas corresponden a la deformación de la columna. Nota que a pesar de que los esfuerzos sean plásticos en la columna, las derformaciones siempre son planas en línea recta transversalmente. En todos los casos se analiza la deformación en el punto de falla del hormigón con una deformación unitaria de εu = 0.003

Las fuerzas Pu y Mu se refieren a las solicitaciones externas que deforman el elemento

Caso 1 La carga es solo de compresión, por tanto la deformación es de compresión y uniforme en toda la sección. En este caso el acero As y el acero As’ toman la misma deformación que el hormigón y son iguales a 0.003

Caso 2 En una situación de fuerzas combinadas de flexión y compresión, el diagrama de deformaciones es inclinado. Sin embargo, las magnitudes de Pu y Mu podrían ser tales que no generen una deformación significativa en los aceros a tracción As, y por tanto al momento de la falla del concreto, el acero a tracción no llega a la fluencia. (Es por eso que en el equilibrio de fuerzas, la fuerza de tracción del acero se representa por As*fs (y no con la expresión As*fy como en el caso de vigas).

Caso 3 Este caso de análisis corresponde a las deformaciones de la sección cuando la columna se comporta más como una viga. En este caso la flexión es predominante y al momento de la falla del hormigón el acero ya habrá fluido. En la gráfica 3 se ve como el acero lleva deformaciones sustanciales al momento de la falla del hormigón. En esta configuración de falla el acero puede tomar deformaciones mucho más grandes que la deformación que logra la falla balanceada (εs= fy/Es y εu = 0.003).

Necesitamos saber qué pasa con el bloque de compresión a partir de estos diagramas. La altura del diagrama de compresión es “a” y está relacionada con la altura al eje neutro “c” de la sección mediante la fórmula a = β1·c . ¿Recuerdas que en un anterior post hablé de que los esfuerzos en la viga están en función de la excentricidad de la carga?. Pues estos esfuerzos también podemos calcularlos en función a la posición del eje neutro.

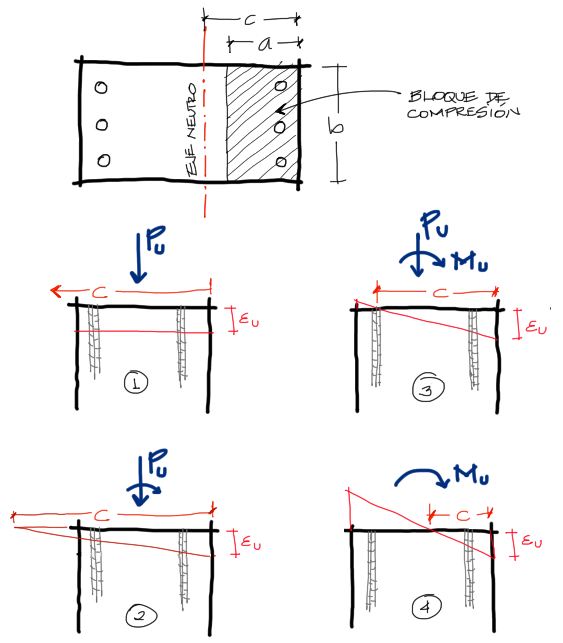
En los cuatro casos vemos como a medida que la flexión aumenta y la carga axial disminuye, el eje neutro pasa de una situación de posición infinitamente lejana a la izquierda de la sección (1) hasta una posición muy cercana a la cara derecha de compresión de la columna (4).

Parametrizando las ecuaciones de Pn y Mn

Si te fijas en las ecuaciones de resistencia Axial y Momento nominales:

Ambas ecuaciones están en función a variables que aun no conocemos:

• La altura del bloque de compresión “a”
• El esfuerzo de los aceros a tracción fs
• El esfuerzo de los aceros a compresión fs’

Por otro lado recuerda que al comienzo del artículo indiqué que las dimensiones h, d, d’ y las secciones de acero As y As’ son conocidas (pues a partir de estas dimensiones intentaremos encontrar la resistencia de la columna).

La forma de conocer estas variables desconocidas es a partrir del diagrama de compatibilidad de deformaciones que mencioné en el anterior subtítulo, de la siguiente manera. Por geometría podemos deducir cuanto se deforma el acero a tracción y el acero a compresión en función de la posición del eje neutro “C” y asumiendo en todos los casos que el hormigón entra en fluencia a una deformación unitaria igual a 0.003 (asumimos que el hormigón entra en fluencia en todos los casos pues llevamos a este material al límite de su compresión. Solo de esta manera podemos establecer que la pieza falla).

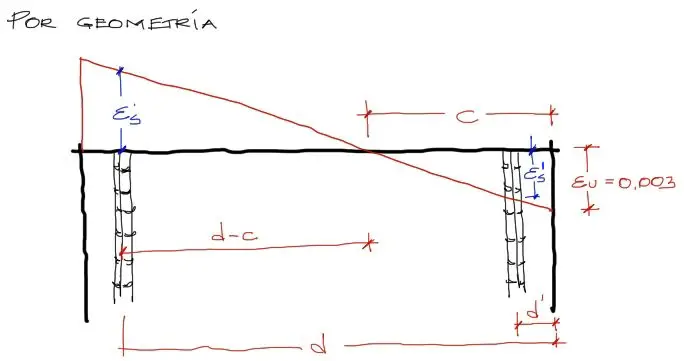
Nos fijamos en el triángulo c-ξu. Todos los triángulos que obtengamos a partir de este triángulo, serán semejantes. Por tanto podemos igualar la relación de los lados de este triángulo con los lados de ξs’-(d-c) y también con el triángulo ξs-(c-d’). Queda entonces:

Luego, sabemos que el esfuerzo es igual al módulo elástico del material E por la deformación unitaria ξ. cambiando las variables para el acero, con Es = módulo elástico del acero = 200GPa, se tiene:

Finalmente reemplazando las penúltimas ecuaciones en estas últimas:

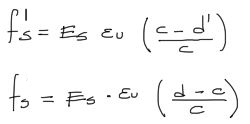
De las últimas ecuaciones ya tenemos los esfuerzos del acero en función de variables conocidas, excepto “c” que es nuestro parámetro variable. La única restricción para este último par de ecuaciones es que ni fs ni fs’ superen el límite de fluencia fy. Si se sobrepasaran debemos utilizar fy en vez de fs en las ecuaciones de Mn y Pn. Finalmente, la variable “a” que al comienzo del subtítulo dijimos que no conocíamos, la podemos conocer en base a la relación entre el eje neutro y el bloque de compresión del concreto:

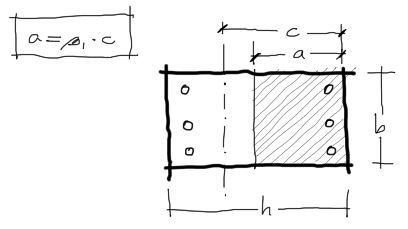
De esta ecuación, la variable β1 está en función a la resistencia característica del hormigón f’c (la figura se muestra a continuación). Por otro lado a no debe sobrepasar la altura h de nuestra sección transversal. Si se sobrepasara, utilizamos “h” en vez de “a”

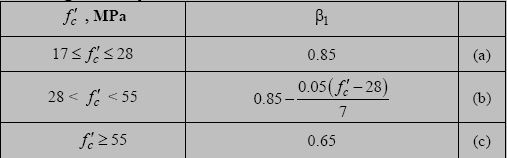
Con todo esto tenemos las fórmulas necesarias para resolver nuestro diagrama de interacción con acero en los extremos de la columna.

En resumen

En resumen el procedimiento a seguir consiste en ir encontrando Mn y Pn en función a las variables debajo de Mn y Pn en las fórmulas abajo. La única variable desconocida “c” la imponemos nosotros desde valores muy pequeños hasta valores tan grandes como 100 [m] si se quisiera. Para cada valor de “c” le corresponde un valor de “Mn” y “Pn”. Se forman entonces pares ordenados [Mn,Pn] que se irán graficando en un sistema coordenado cartesiano.

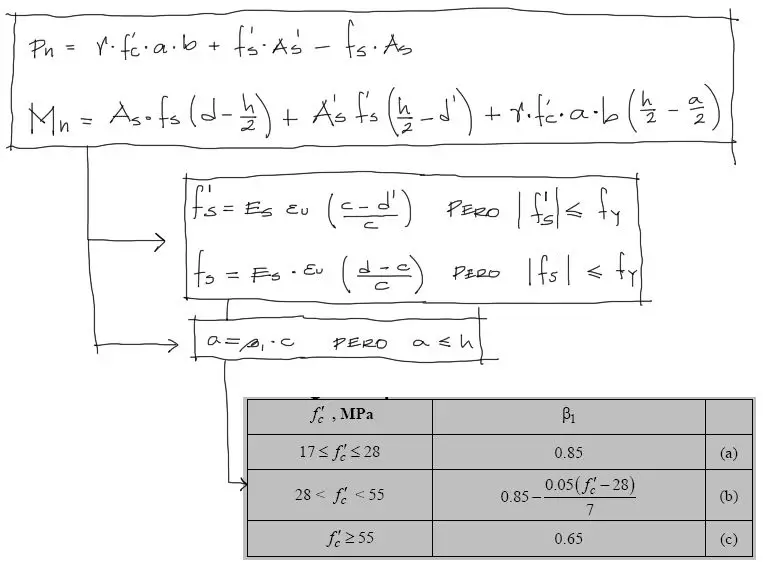
Graficando

Los puntos que se vayan formando deberán adoptar la forma como se muestra en la siguiente imagen:

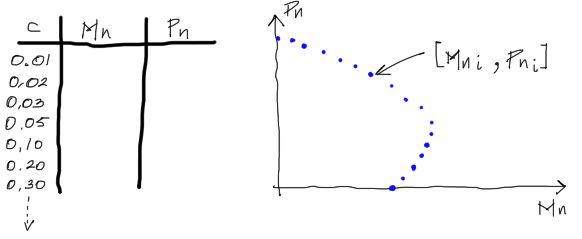
En una siguiente publicación haré un ejemplo gráfico de toda la teoría explicada

Factores de seguridad

Además de todo el procedimiento mencionado, deben aplicarse factores de seguridad a la resistencia nominal [Mn,Pn] de la columna. Al tratarse de un elemento que en caso de colapso pone en riesgo la integridad de toda la estructura, estos factores de seguridad reducen la resistencia de la columna casi a la mitad. Por ejemplo en el caso de vigas los factores de reducción de resistencia son de ø=0.9 en cambio para nuestro estudio de columnas con predominante compresión axial, el factor de seguridad será de ø=0.65 multiplicado además por 0.8 para salvar excentricidadaes no previstas. De esto se hablará en más detalle más adelante.

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE HORMIGÓN ARMADO←←←