Antecedentes

Antes de leer este artículo se deben haber leido o repasado el artículo Vigas T – Consideraciones Iniciales. Lo que se garantiza a partir del enlace nombrado es que la viga T esté adecuada en medidas del Ala y en cuanto a la cantidad máxima de acero a flexión con la que se puede reforzar a dicha viga.

Una vez verificada la sección efectiva de la viga T (ancho máximo y altura mínima de las alas de la viga) y conseguida la cantidad de acero máximo a flexión con la que se puede reforzar la viga, estamos en condiciones de comenzar a diseñar la cantidad de acero necesaria a flexión que llevará la viga para solicitaciones “Mu” generadas a partir de las cargas.

Solicitación “Mu”

A partir de lo que se analizó en el anterior artículo, hasta el momento no se ha utilizado para nada el dato de la solicitación a flexión Mu producto de las cargas en la viga.

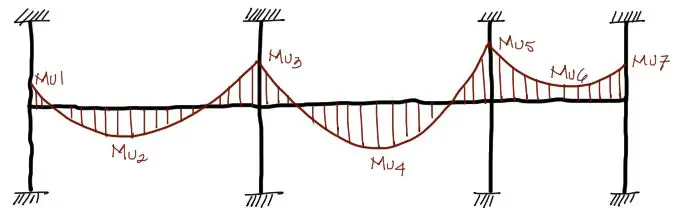
Conviene resaltar en este punto que a diferencia de las vigas rectangulares, en el caso de vigas T conviene diferenciar el sentido o la dirección de la flexión. Si bien en vigas rectangulares la flexión podía ser positiva o negativa y solo había que alternar el acero de diseño en función a la dirección del momento flector, en vigas T no es tan sencillo.

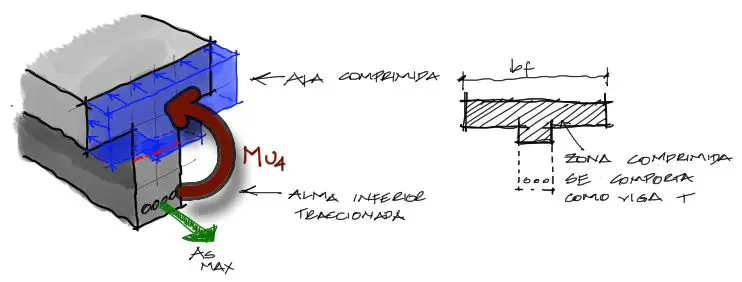
En una viga T si el momento a flexión es positivo estamos ante una situación donde la viga se tracciona inferior del alma y se comprime el ala. En este caso el análisis de la viga como sección T es totalmente apropiado.

Sin embargo si el momento fuera negativo para una viga T, lo que se comprime es la parte inferior del alma y la zona de tracción es todo el sector superior donde se encuentra el Ala. En estos casos la viga debe ser tratada como una viga rectangular cuyo ancho de viga ya no es el ancho del ala “bf” sino el ancho del alma “bw”.

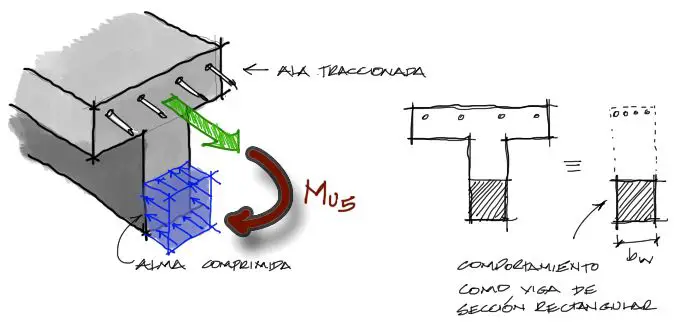
Teniendo todo esto en cuenta, procedemos con el diseño de las vigas T cuya zona de compresión se encuentre en todo el ancho del ala “bf”. Para momentos flectores que compriman la parte inferior del alma, referirse al Diseño a flexión de vigas rectangulares.

Diseño de acero a flexión

El diseño a flexión de vigas T de concreto tiene dos caminos, igual que en el caso de la verificación del acero máximo As-max del anterior artículo. El primer caso de análisis consiste en una situación de esfuerzos de la viga donde Mu solicitará el bloque de compresión con una altura “a” más pequeña que “hf”. El segundo caso de análisis se da cuando los momentos solicitantes Mu son tan fuertes que comprimen una zona de la viga que es tan grande que abarca una altura de compresión más alta que “hf”.

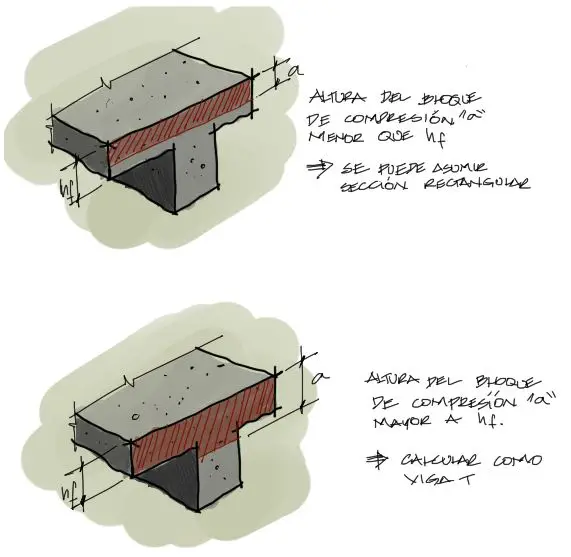
Se debe primeramente calcular la cantidad de acero que debería llevar la viga producto de la solicitación Mu como si la viga fuera una sección rectangular de ancho constante “bf”. A partir de este análisis una vez determinada la cantidad de acero “As” que resista a “Mu”, se verifica si la altura del bloque de compresión “a” es más pequeño que la altura del ala “hf”. Si fuera este el caso, se deja el análisis como está y “As” es la sección de acero a utilizar en el diseño. Si sucediera lo contrario debe hacerse un ajuste al bloque de compresión, como se verá más adelante.

Cuando “a” es menor a “hf”

Esta es la primera situación mencionada. Como por debajo de la zona de compresión del hormigón sombreada se supone que la viga está agrietada y trabajando a tracción, no importa la forma de la viga por debajo de la profundidad “a”. Por tanto puede analizarse la viga como si fuera rectangular. Veamos como realizar el análisis de viga imaginando que toda la viga es de ancho constante “bf”

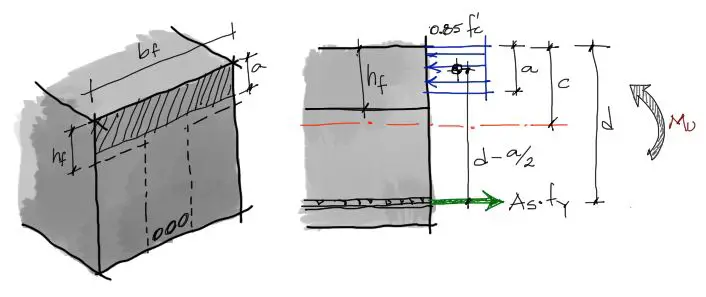
En este análisis aún no conocemos la profundidad de la cota “a” ni la cantidad de acero que llevará la viga. Lo que si conocemos son las dimensiones de la sección transversal, las resistencias adoptadas para el análisis f’c y fy, y por último conocemos la solicitación a momento flector Mu a partir de los diagramas de momento flector.

Las incógnitas “a” y “As” se calculan simultaneamente a partir de un sistema de dos ecuaciones con dos incógnitas. Estas dos ecuaciones se obtienen del equilibrio de suma de fuerzas horizontales y de la sumatoria de momentos de fuerza.

Estas dos ecuaciones pueden resolverse reemplazando “a” despejado dentro de la segunda ecuación como se muestra a continuación. Este reemplazo genera una ecuación de segundo grado donde la incógnita es As.

Esta ecuación de segundo grado puede resolverse mediante la famosa solución de ecuaciones de segundo grado mostrada arriba, donde los coeficientes de As², As, 1 son respectivamente los correspondientes a “a”,”b”,”c” en la ecuación de segundo grado. Se aplican los coeficientes a la solución y se obtiene la solución de As (Se toma la solución más pequeña, lo que corresponde a omitir la solución con el signo positivo en la raiz).

A partir de la solución de As ya podemos conocer la altura del bloque de compresión del concreto “a” reemplazando As en la primera ecuación:

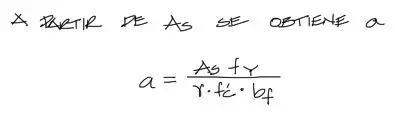
Finalmente corresponde hacernos la pregunta: ¿Es “a” más pequeño que “hf”? Si es afirmativa, el cálculo termina ahí. Si la respuesta es negativa, debemos continuar con el siguiente ajuste.

Cuando “a” es mayor a “hf”

En este caso, la forma del bloque de compresión toma una figura compuesta de rectángulos de diferente altura.

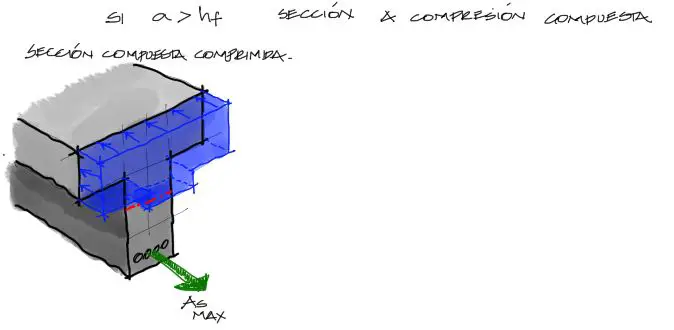
Al igual que en el anterior artículo de consideraciones preliminares, aquí dividiremos la zona comprimida en dos. Una zona comprimida compuesta por el Ala de la viga, y otra por el alma de la viga.

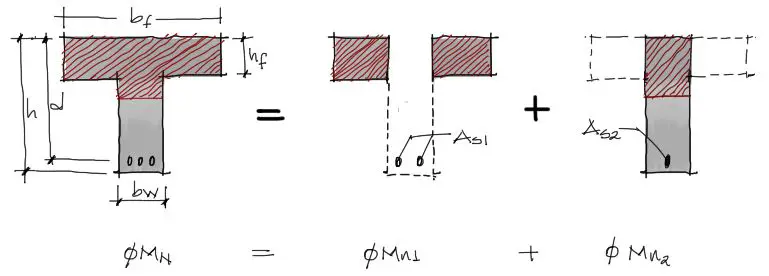
Estas dos fases separadas de la viga hacen el cálculo de la cantidad de acero mucho más sencilla. La suma de los pares compresión-tension de ambas fases resistirán respectivamente con Momentos Flectores nominales Mn1 y Mn2 respectivamente, factorizados por Ø=0.9 para flexión. La suma de ØMn1+ØMn2 será igual a la resistencia a momento flector de toda la viga.

Como estamos diseñando la viga para que la resistencia a momento flector sea igual al momento solicitante, entonces reemplazamos ØMn por Mu.

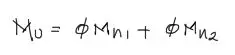
De esta ecuación se conoce por el momento solo Mu. ØMn1 y ØMn2 son incógnitas que trataremos de la siguiente manera.

Cálculo de ØMn1

ØMn1 que es la resistencia aportada por el Ala comprimida y la cantidad de acero As1 puede determinarse fácilmente a partir de que sabemos que toda el ala está comprimida, y su resultante puede calcularse multiplicando área achurada por esfuerzo a compresión. Esta resultante debe ser igual a la resultante a tracción del acero y luego despejamos As1.

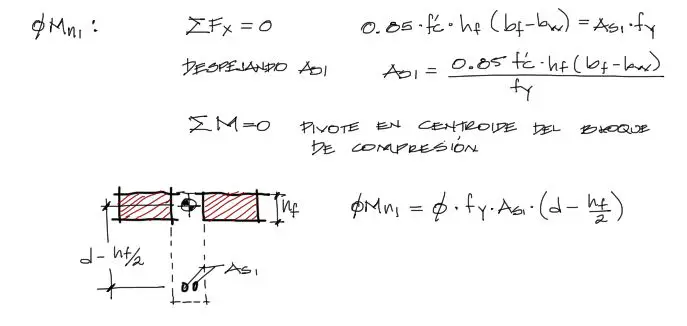
Con As1 conocido, ya se puede entrar al equilibrio de momentos, donde ØMn1 debe ser igual al par generado por las resultantes a compresión y tracción. Convenientemente se puede escoger el centroide del bloque de compresión como pivote de la suma de momentos, y así el momento resistente ØMn1 es igual a la resultante de fuerzas As1*fy multiplicada por el brazo (d-hf/2).

Cálculo de ØMn2

Conocidos entonces Mu y ØMn1, se los despeja de la ecuación Mu=ØMn1+ØMn2. Este momento ØMn2 deberá ser resistido por el par de compresión del alma de la viga y As2.

Al igual que con vigas rectangulares, podemos formar un sistema de dos ecuaciones (suma de fuerzas horizontales y suma de momentos) con dos incógintas “a” y “As2”, como se muestra a continuación:

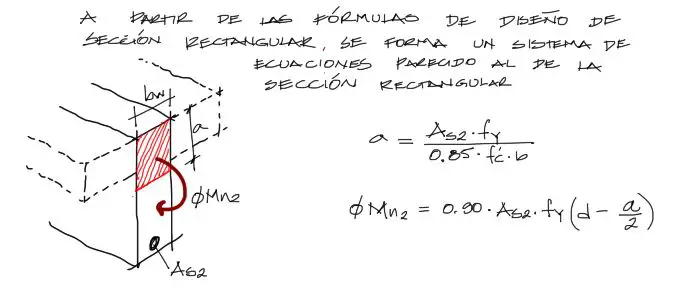
Se resuelve el sistema generando la ecuación de segundo grado con incógnita As2 como analizamos líneas arriba, de donde As2 es la expresión mostrada a continuación:

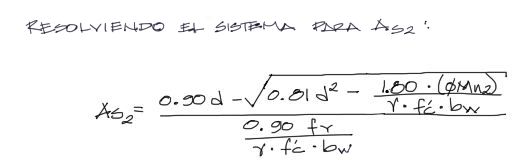
Finalmente la cantidad de acero que debe llevar la viga T consiste en la suma de los aportes de As1 y As2,

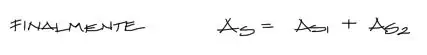
y con esto termina el cálculo de cantidad de Acero a flexión para una viga T.

Programa

En el siguiente enlace puedes utilizar un programa que te permite calcular automáticamente el acero a flexión de vigas T.

– PROGRAMA DE CÁLCULO DE ACERO A FLEXIÓN EN VIGAS T

Qué sigue?

Además del diseño a flexión corresponde hacer el cálculo de resistencia a cortante y diseño de estribos de la viga. Sin embargo eso se tratará en otra publicación.

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE HORMIGÓN ARMADO ←←←