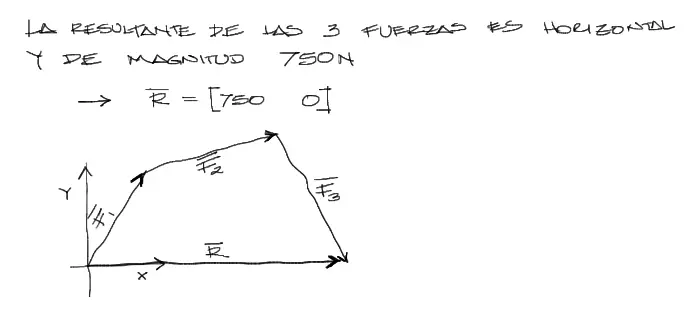
Enunciado
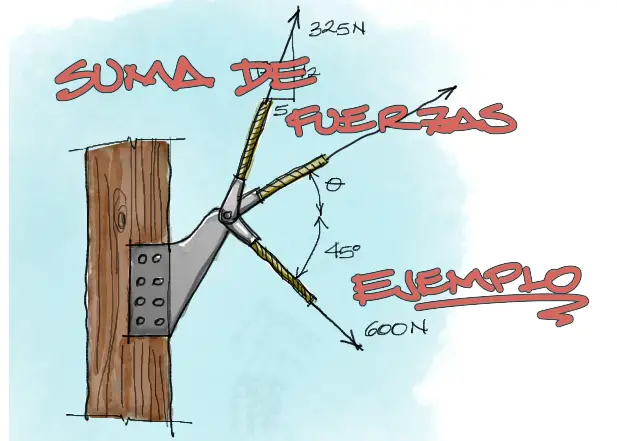
Resolver la fuerza F y la dirección θ del vector mostrado en la imagen de tal manera que la resultante de las tres fuerzas mostradas sea completamente horizontal y de magnitud 750[N]
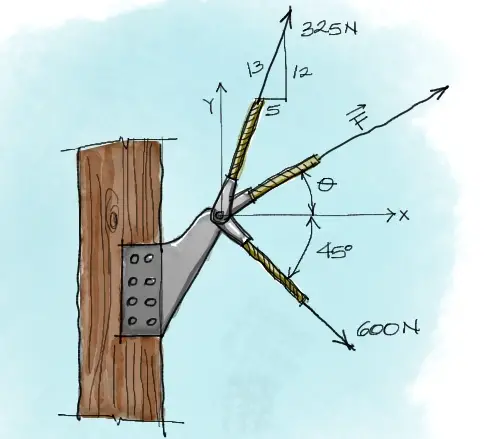
Resolución
Por simplicidad nombraremos a los vectores en orden de arriba hacia abajo como F1, F2, F3:
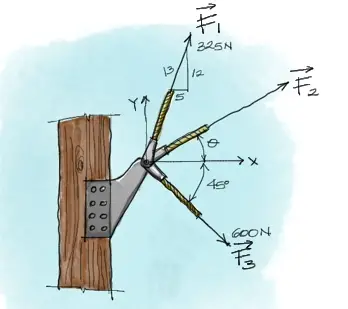
El siguiente paso es descomponer en componentes cada vector.
Componentes de F1
Por proporción de triángulos se tiene

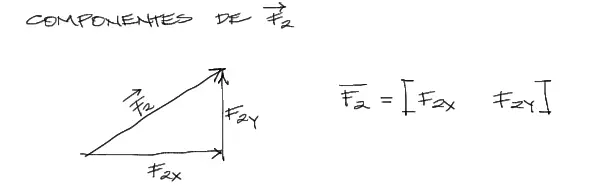
Componentes de F2
Como el vector F2 es desconocido, podemos conservar sus componentes como incógnitas F2x y F2y
Componentes de F3
La descomposición trigonométrica correspondiente a partir del ángulo de 45 es sencilla. Se debe tomar en cuenta sin embargo que luego de descomponer el vector, la componente Y del vector F3 debe tomar signo positivo en la notación vectorial entre corchetes.
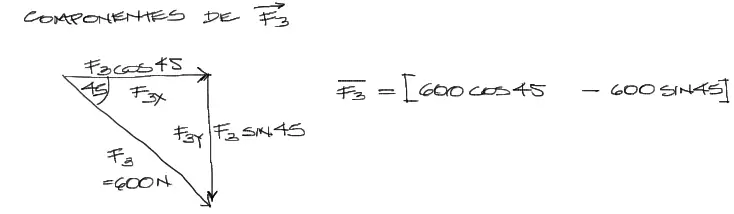
Razonamiento del problema
Se debe leer entre líneas que lo que el enunciado nos indica es que la componente Y de la fuerza resultante es igual a cero, ya que esta fuerza R es completamente horizontal. Además su magnitud es de 750N, entonces queda:
Suma de componentes
La suma de vectores es igual a la suma de sus componentes, por tanto hacemos la suma de las componentes en X y la suma de las componentes en Y de los tres vectores e igualamos estas sumas a las componentes de R

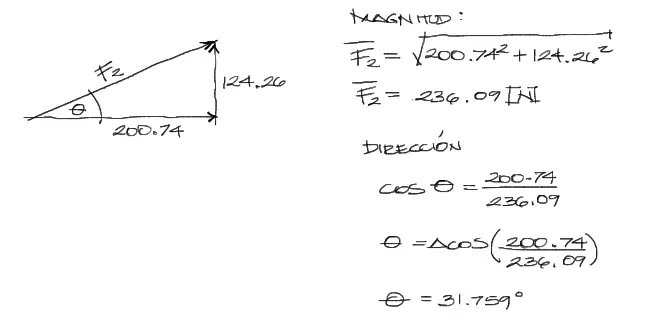
Despejando las incógnitas F2x y F2y se tienen los resultados mostrados arriba. Con estas componentes ya podemos obtener el módulo y dirección del vector F2 fácilmente.
Módulo y Dirección de F2
A partir de pitágoras obtenemos la magnitud de F2, y a través de cos(θ)=catetoAdyacente/hipotenusa obtenemos θ:
autor: Marcelo Pardo