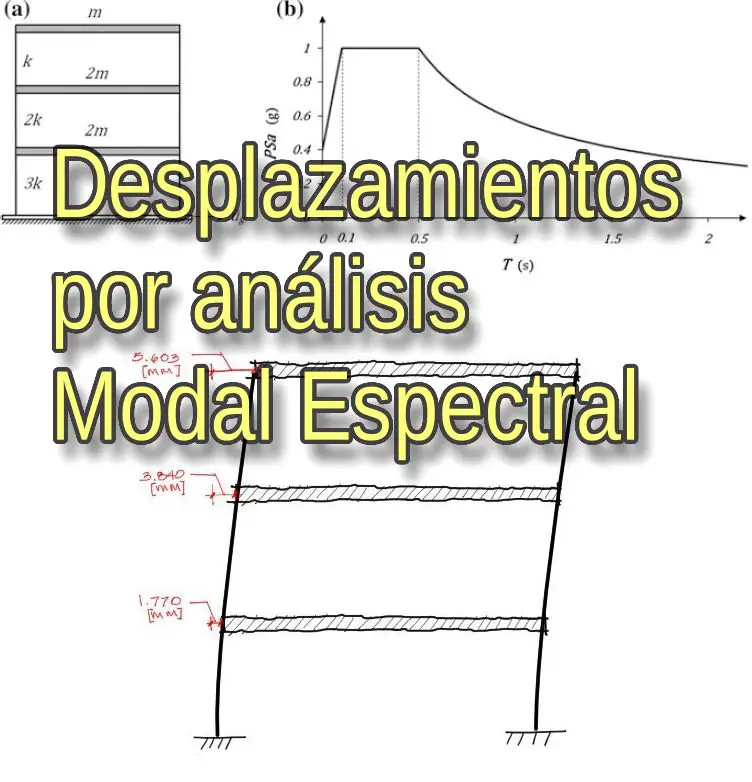
Enunciado

Este ejemplo está reproducido del libro “BASIC EARTHQUAKE ENGINEERING – SUCUOGLU AKKAR.

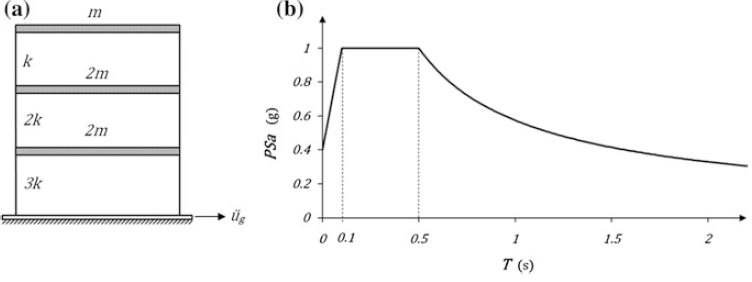
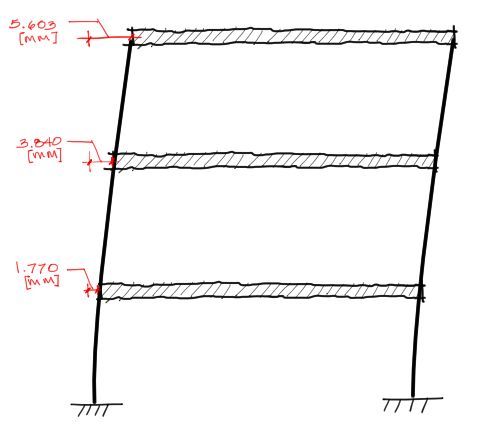
Se piden resolver los desplazamientos máximos de la estructura mostrada abajo, a partir del espectro de respuesta mostrado también en la gráfica.

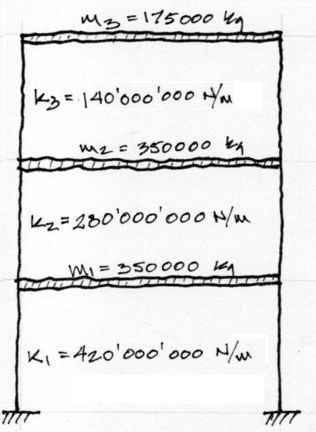
La rigidez de las columnas k = 140000 KN/m entendiendose a k como la rigidez de las dos columnas. La masa de los diafragmas es m = 175000 kg.

Solución en vídeo

Solución

El libro comienza proporcionando los valores y vectores propios de inicio. Sin embargo nosotros calcularemos todos estos valores desde cero.

Valores y vectores propios

Para comenzar, debemos homogeneizar las unidades en las cuales se nos proporcionan las rigideces y las masas. Las unidades de rigidez deberían estar derivadas de las unidades de masa multiplicadas por la gravedad. En nuestro caso si la masa está en [kg] y la gravedad en [m/s2], la rigidez debería trabajarse en Newtons. Por tanto:

Luego armamos las matrices de masa y de rigidez:

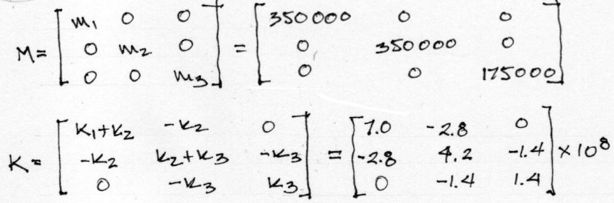
Estas matrices se arman a partir de teorías del método de rigidez.

La ecuación de movimiento homogénea (sin cargas externas) y sin considerar amortiguamiento, obtenida del análisis dinámico es la siguiente:

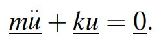
A partir de esta ecuación se obtienen los valores y vectores propios de la estructura. Estos valores propios y vectores propios responden a la solución del polinomio característico obtenido del determinante de la siguiente ecuación:

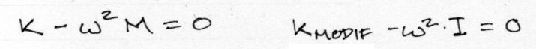
La expresión de la izquierda sin embargo, se puede modificar dividiendo la fila 1 entre la masa1, la fila 2 entre la masa 2 y así sucesivamente. De esta manera se obtiene un sistema equivalente como el de la derecha donde la matriz que acompaña a “ω” es la matriz identidad, y esta nueva expresión ya puede ser resuelta por algoritmos ya desarrollados.

Matricialmente el procedimiento descrito se ve como sigue:

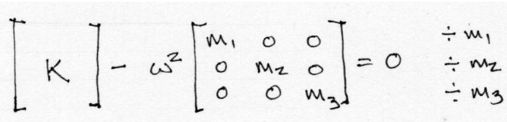
Hechas las correspondientes divisiones, resolvemos los Eigenvectores del sistema:

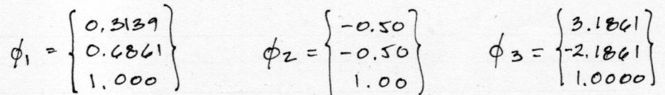
Asimismo los valores propios o Eigenvalores, una vez aplicada la raíz, son los siguientes:

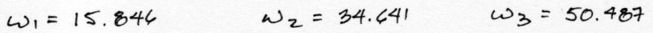
El término “ω” es la llamada frecuencia natural circular de vibración del sistema. Sus unidades son de radianes/segundo. A partir de esta frecuencia se pueden obtener los periodos naturales de vibración de la estructura son:

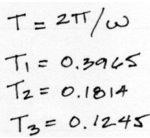
Normalización de masas

La normalización de las masas es una práctica conocida en el cálculo dinámico, que ayuda a reducir operaciones aritméticas. Las masas modales se obtienen a partir de la multiplicación del Eigenvector fila por la matriz de Masa y luego por el mismo Eigenvector en columna. operando se tiene:

Para las otras masas modales se repite el proceso:

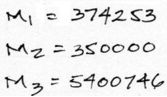
Factores de excitación modal

Al igual que con las masas modales, los factores de excitación modal se obtienen para simplificar operaciones aritméticas al momento de calcular las solicitaciones o deformaciones finales del sistema. Se denotan por la letra “L” y se obtienen a partir de la multiplicación del Eigenvector fila, por la matriz de masas y por el vector columna de unos. Numéricamente:

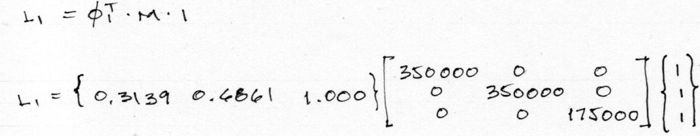
Repitiendo operaciones con todos los factores:

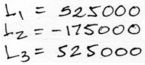
Desplazamientos máximos

Los desplazamientos máximos obtenidos para cada modo se pueden obtener a partir de la siguiente expresión:

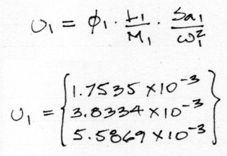
En la expresión mostrada todos los términos son conocidos, exceptuando la pseudo aceleración Sa1. El valor de Sa1 se obtiene a partir del espectro de respuesta del enunciado arriba mostrado. Para el periodo natural de vibración T1, T2 y T3, la pseudo Aceleración Sa1, Sa2 y Sa3 respectivamente son 1, 1 y 1. Con todos estos datos el reemplazo es directo. Para los desplazamientos máximos de los modos de vibrar 2 y 3 sucede algo similar:

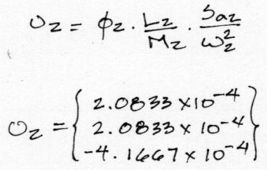
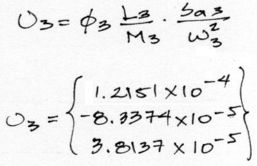
Las unidades de estos desplazamientos están en las mismas unidades en las que se operaron todos los datos. en este caso están en [m].

Desplazamiento Modal Espectral

Los desplazamientos modales espectrales de cada nudo para el diseño de la estructura se obtendrán mediante el método SRSS (Square Root of the Sum of the Squares). En español significa la raiz cuadrada de la suma de cuadrados. Consiste en la raiz cuadrada de la suma de los cuadrados del desplazamiento de cada modo, para cada nudo. Matemáticamente:

Gráficamente esto se ve de la siguiente manera

Estos son los desplazamientos que deberán utilizarse para el diseño de la estructura.

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE DISEÑO SÍSMICO ←←←