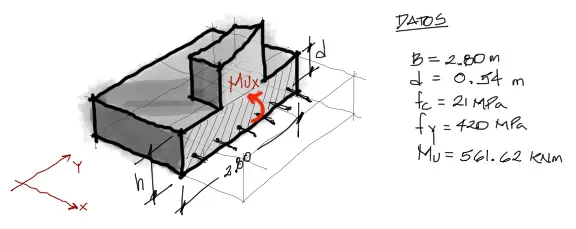
Datos del problema
Esta es la continuación del diseño de una zapata concéntrica muy básica.
En la primera parte del diseño se determinó la dimensión de la base de la zapata para que el suelo resista la carga Pserv. Todo el detalle de este análisis lo encuentras en:
Ejemplo de diseño de base de zapata Concéntrica.
Ahora abordaremos el diseño a flexión de la zapata. Para eso necesitamos los siguientes datos de la imagen
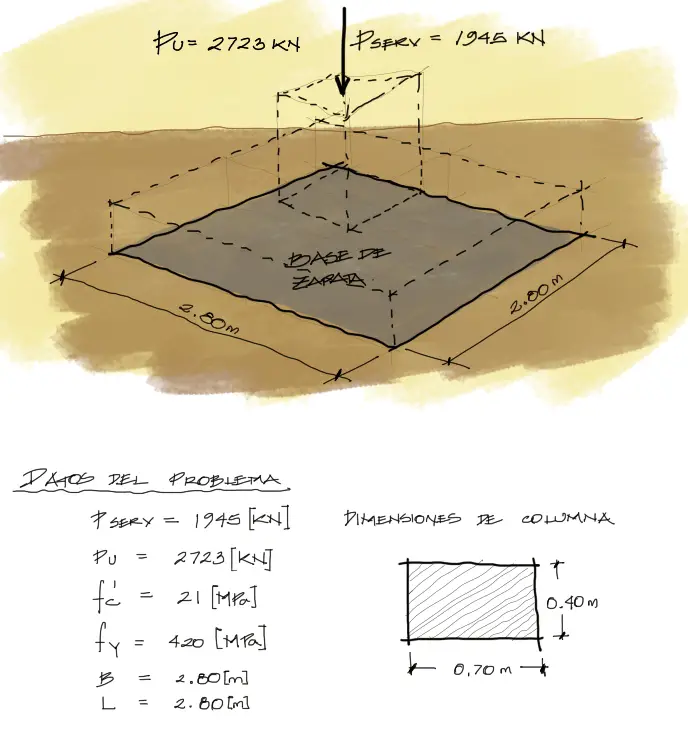
Aparecen nuevos datos más allá de los datos necesarios en el anterior artículo de diseño de la base de la zapata. Esto se debe a que en el diseño de las dimensiones de base no se necesitaban resistencias de ningún otro material más allá de la resistencia del suelo.
En este artículo además de la carga de servicio de la columna, utilizaremos las cargas mayoradas axiales Pu que llegan de la superestructura. Además necesitamos resistencias de acero y concreto. Ṕara estos materiales escogeremos resistencias típicas de 420MPa y 21MPa respectivamente.
Altura de zapata
La altura a usar de la zapata no es un dato. Debemos determinarla nosotros en base un poco a la experiencia y un poco en base a reglas sencillas de proporciones. Para zapatas prismáticas como la que utilizaremos en el diseño, una zapata debe tener un peralte de aproximadamente 1/5 de la base.
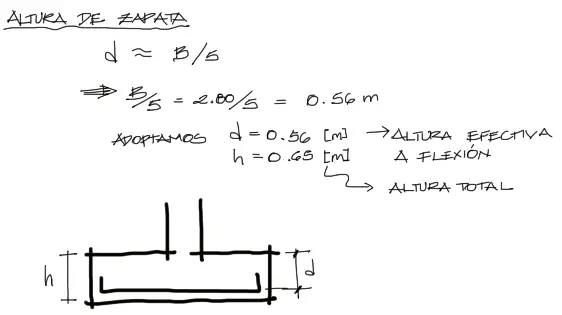
En este caso se obtiene a partir de esta relación, una altura o peralte de zapata de 0.56m. Este resultado es solo una referencia, pudiendose adoptar dimensiones ligeramente mayores o menores a 0.56 para la altura efectiva de la losa. En este caso adoptamos este mismo resultado como altura efectiva “d”. Para la altura total de la losa o zapata adoptamos 0.65m.
Puede impresionarte la cantidad de recubrimiento de hormigón que existe entre la base de la zapata y el eje de los aceros, sin embargo para fundaciones el recubrimiento de hormigón a la cara del acero debe ser de 7.5cm mínimamente. Si a estos 7.5cm le sumamos un radio promedio de acero de 1cm, ya tenemos 8.5 de distancia de la base al eje de aceros. Nosotros tomamos 9cm por redondear.
Momento de Flexión en la Zapata
Las zapatas cuadradas deben diseñarse a flexión en ambas direcciones. El problema podría parecer simétrico sin embargo debido a las dimensiones disparejas de la columna, se debe realizar un análisis separado en cada dimensión.
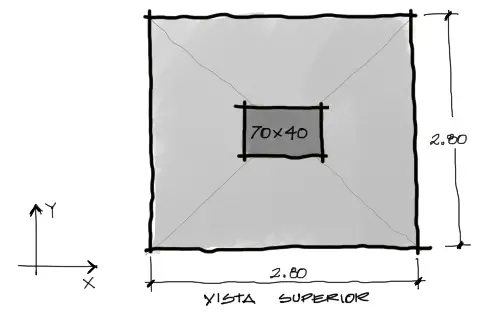
En la imagen arriba se ve que la columna es de dimensiones de 40×70 centímetros, por tanto debemos analizar la flexión crícita de la zapata en las dos caras de la columna, como se muestra en la siguiente imagen:
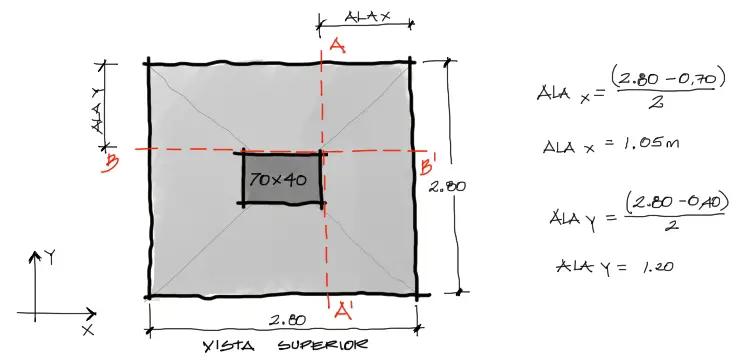
Por simple geometría podemos calcular las Alas o voladizos en cada dirección a partir de las caras de las columnas. La diferencia de distancias de 1.20 y 1.05 hacen que las magnitudes de flexión sean distintas también en cada dirección.
Flexión en el Ala Y
Realizamos un dibujo del perfil de la zapata en esta dirección, como se muestra en la imagen siguiente. El ala Y está sometida a una carga igual al esfuerzo de reacción del suelo hacia la estructura.
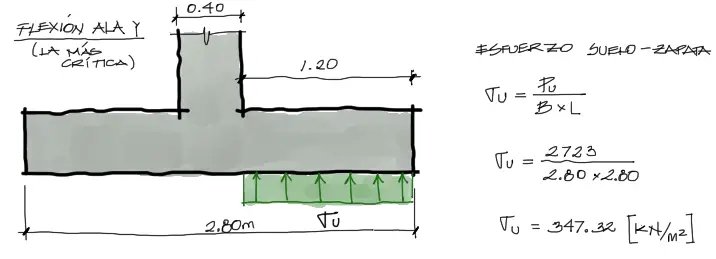
Debido a que ahora estamos en un diseño de una pieza de hormigón, debemos utilizar las cargas mayoradas o cargas últimas Pu=1.2D+1.6L de la estructura. Este valor es un dato proporcionado al inicio del artículo y que fue obtenido a partir de un análisis estático del pórtico de la estructura.
En este caso la carga sobre el Ala Y es el esfuerzo producto de la carga de la columna dividida entre toda la superficie de la zapata, y da como resultado un esfuerzo de 347.32 KN/m2.
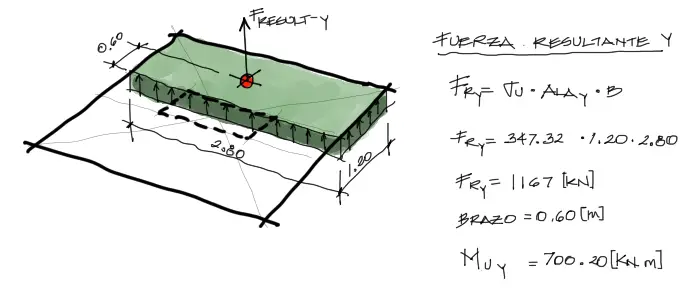
Este esfuerzo debe multiplicarse por la superficie del AlaY para encontrar la resultante de fuerza aplicada sobre el Ala. Posteriormente calculamos el momento flector igual a la resultante por el brazo, según el siguiente análisis:
Diseño de acero para la dirección Y-Y
Habiendo calculado el momento flector, tenemos todos los datos para el cálculo de acero en la zapata. Obviamente la flexión genera tracción en las fibras inferiores de la zapata y en consecuencia, acero inferior.
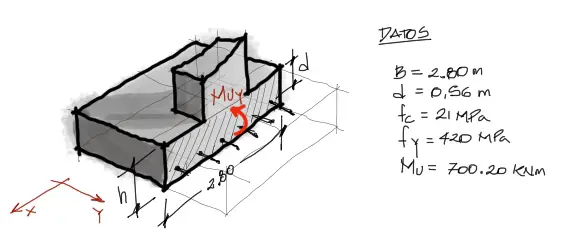
Podemos para el diseño a flexión valernos de un pequeño programa que escribí y que nos entrega directamente la cantidad de centímetros cuadrados de acero a flexión en función a los datos de la imagen anterior. El programa lo encuentras en Programa de flexión de losas de Hormigón Armado. Se reemplazan entonces los datos:

Se obtienen entonces 33.94cm2 de acero necesarios. Para zapatas de las dimensiones analizadas, conviene el uso de acero de 16mm. De esta manera se obtiene un espaciamiento entre barras de al rededor de 20cm más o menos. Espaciamientos menores a 15cm y mayores a 30cm no son tan adecuados.
El programa nos entrega el área neta de acero necesario. Para traducir esta cantidad de acero en número de barras, podemos obtener a partir de la tabla de SECCIONES DE BARRAS DE ACERO. A partir de esas tablas, una barra de ø16mm tiene una sección de 2.01cm2. La cantidad de barras necesarias se obtiene de la división de AsTotal/As1ø16 y se redondea al techo superior.
Flexión en el Ala X
Un análisis similar puede realizarse para la dirección X de la zapata. Nota que el “voladizo” o distancia del Ala X en este caso es menor a la dirección en Y. Entonces es natural pensar que la flexión en esta dirección también será menor.
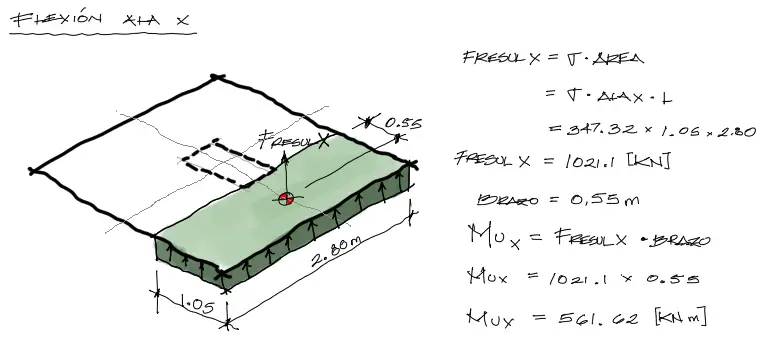
Diseño de acero en la dirección X-X
El momento flector obtenido en esta dirección es de 561.62[KNm]. Ya que el acero en esta dirección no puede ir exactamente a la misma altura que el acero en la dirección Y, se lo pone justo encima. Debido a esta sobreposición, la altura efectiva del acero en esta dirección será ligéramente menor a la altura d=56cm. Ya que estamos utilizando acero de 16mm, debemos restarle dos radios de 1cm a nuestra altura efectiva quedando en la dirección X-X una altura efectiva de análisis a flexión de d=54cm. Para esta altura y con todos los datos ya conocidos se tiene:
Reemplazando nuevamente los datos en el programa, se tienen los siguientes resultados:

En este caso el acero mínimo es mayor al acero As obtenido por flexión. En este caso entonces se debe utilizar el Acero mínimo como acero de refuerzo. Cabe recalcar que el acero mínimo de zapatas es el mismo acero mínimo de losas llenas y es igual a 0.0018*420/fy*b*h.
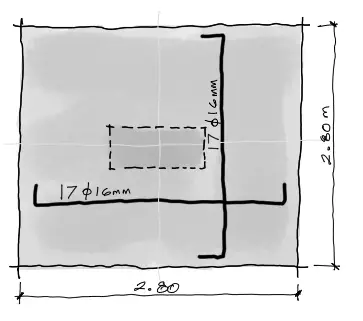
Dibujo de refuerzo
Tras todo el análisis realizado se debe siempre dibujar la distribución de acero en el elemento:
Qué sigue
El trabajo de diseño no concluye aquí. Deben realizarse dos verificaciones a cortante. Si las verificaciones a cortante no cumplieran con la resistencia se debe incrementar la sección o peralte de estas zapatas.
autor: Marcelo Pardo



Buenas tardes inge. Espero todo vaya bien.😎
Solamente con una pregunta respecto a la Flexión en el Ala X.
El Brazo está propuesto como 0.55m ¿Es correcto ese dato? Tengo la impresión de que es 0.525m.
¡¡Saludos!!
Miguel tienes toda la razón!! Eres mi corrector más eficiente! jjeje! lo cambiaré. Muchas gracias
Ingeniero, muy buen día.
Con un par de preguntas sobre este tema.
1.- ¿Los esfuerzos de reacción deberían tomarse como un esfuerzo en forma trapezoidal o en la forma uniformemente distribuido como lo propones?
2.- ¿Será que no es necesario obtener excentricidades en X e Y?
De antemano muchas gracias.
Inge Marcelo, muuuuchas gracias por el aporte de tanto conocimiento y sugerencias. Ojalá Dios te dé tiempo y ganas para seguir con esta labor.
Por otro lado, quiero hacerte unas preguntas y, si tu tiempo te lo permitiera, esperaría las puedas leer y apoyarme con tus sugerencias:
1.- Los datos de este ejemplo vienen de https://marcelopardo.com/ejemplo-diseno-base-zapata-capacidad-portante/
¿Por qué la cohesión es igual a cero (0)?
2.- Revisando algunos autores, como McCormac o Nilson, he visto que la metodología que utilizan para el cálculo de aceros
y concreto en zapatas es un tanto diferente. ¿Quién propuso la metodología que nos expones en este ejemplo y las
subsiguientes revisiones de “d”?
3.- Si me salen dos diámetros diferentes, es decir si tengo 17 varillas de 16mm en un sentido y 11 varillas de 20mm en el
otro sentido. ¿Cuál parrilla iría arriba de la otra?
4.- ¿Cómo calculas el área de acero máximo?
De antemano muchas gracias.
Miguel buenas tardes. respondo a tus preguntas.
1) La cohesión es cero porque el suelo es de clasificación Granular
2) Justamente la metodología que utilizo es la de esos libros para el diseño de acero. Qué método proponen esos autores? tal vez lo pasé por alto
3) El acero que va abajo siempre es el que recibe más momento solicitante
4) Está en función a la cuantía máxima.
Un saludo!!
Buenas tardes ingeniero.
Gracias por responder. Respecto al inciso 2), yo no había notado que es exactamente igual, el cálculo del momento y la cantidad de acero, respecto a lo que propone McCormac, lo que pasa es que me confundió la manera en que él lo hace.
Él propone utilizar Mu/(phi*b*d^2) y eso le da un esfuerzo en “psi” que después busca un valor de “rho” que están tabulados en unas tablas al final de su libro, para comparar con el “rho” mínimo por flexión. Pero básicamente es lo mismo. Ahora, McCormac si propone utilizar el acero mínimo a flexión como acero mínimo en zapatas. Y no como lo indica el ACI que propone el acero mínimo por contracción y temperatura.
¡¡Saludos ingeniero!!
Miguel buenas tardes: interesante lo que mencionas del acero mínimo de zapatas. voy a revisarlo. Muchas gracias!