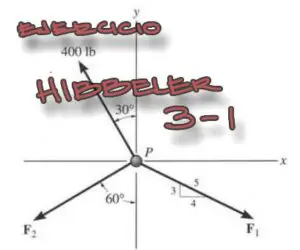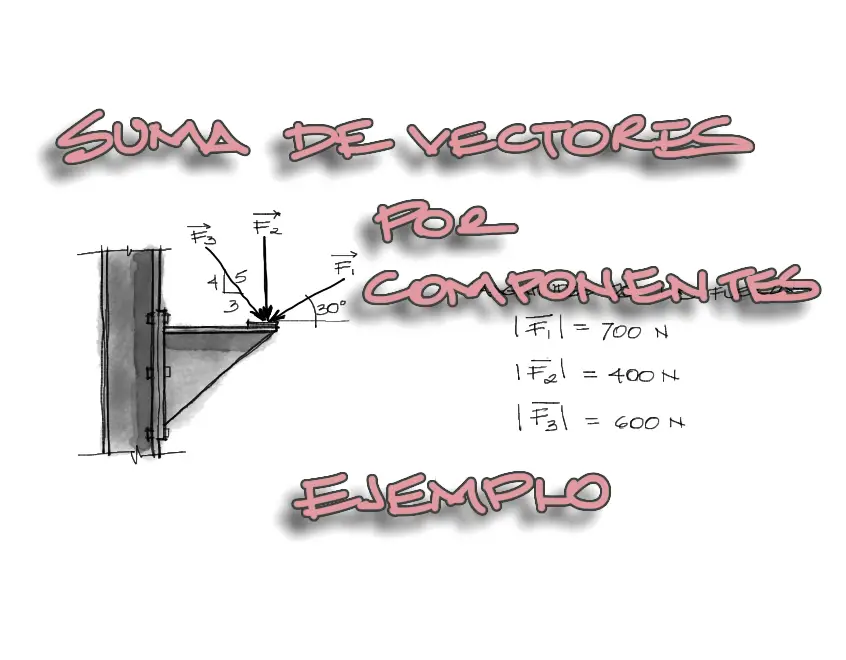
Enunciado
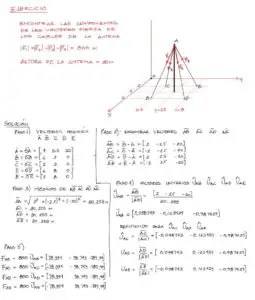
Encontrar las componentes de los vectores F1, F2, F3. Luego encontrar la resultante de las tres fuerzas, así como su magnitud y la dirección medida desde el eje X positivo

resolución
Componentes de las fuerzas
Si bien podemos obtener directamente las componentes de los tres vectores, es mejor graficarlos de nuevo y además con el punto de aplicación del vector en la cola del mismo y apuntando en la dirección del enunciado. Así no hay confusión en la dirección de las componentes del vector resultante. se tiene entonces:
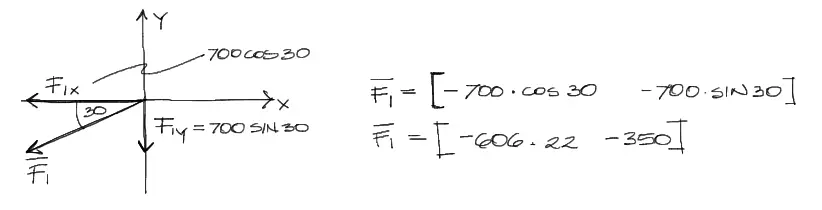
El vector F2 apunta hacia abajo, así sus componentes son simplemente:

Finalmente para el vector F3, debemos trabajar con triángulos semejantes, por tanto usamos las relaciones:
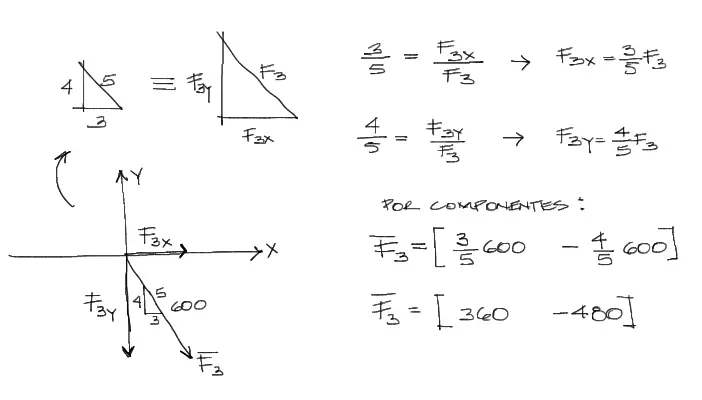
En los 3 casos se debe tener presente la dirección de las componentes a partir de los gráficos: o sea, positivas si las componentes apuntan hacia la derecha o arriba, y negativas si las componentes apuntan abajo o izquierda.
Suma de fuerzas
La suma de las fuerzas es la suma de las componentes. El cálculo es directo
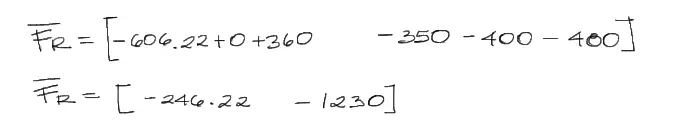
Módulo de la fuerza resultante
Obtenidas las componentes del vector resultante, el módulo del vector se obtiene a partir de pitágoras:
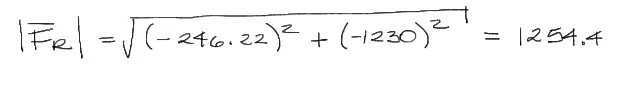
Dirección de la fuerza resultante
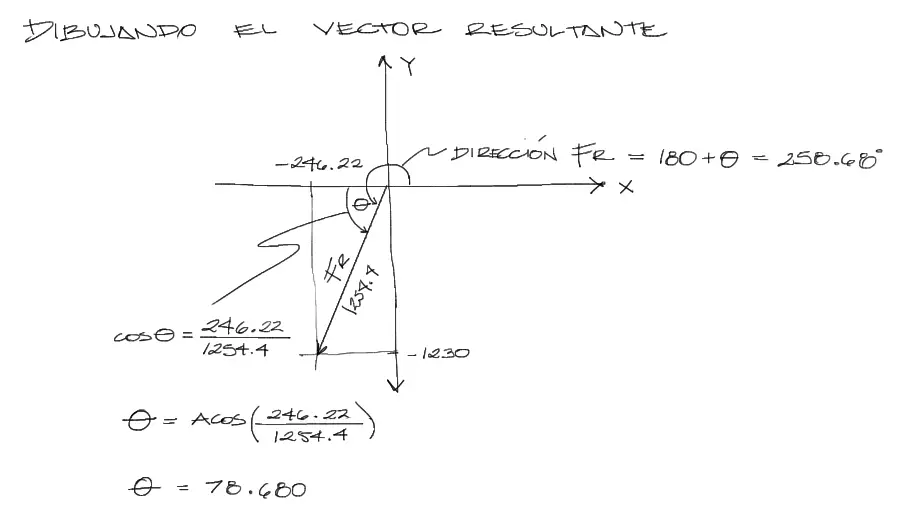
Antes de obtener el ángulo medido desde el eje X positivo, es conveniente obtener el ángulo TITA que es finalmente un ángulo agudo, fácil de calcular a partir de funciones trigonométricas desde la relación con el ángulo y el triángulo que lo contiene. Entonces conformamos el triángulo del ángulo “tita” primeramente, obtenemos su magnitud por cosenos, y finalmente a este ángulo tita le sumamos 180°
autor: Marcelo Pardo