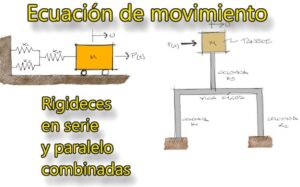
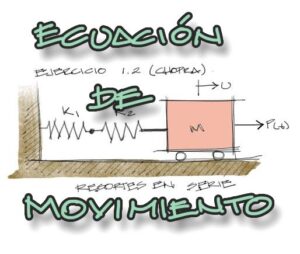
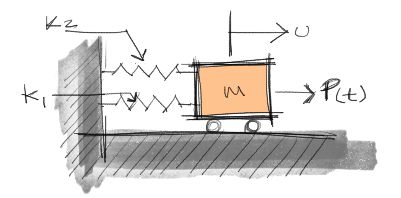
Enunciado
Determinar la ecuación de movimiento (y la rigidez del sistema) para el sistema mostrado en la imagen.
este es el ejercicio 1 del tema 1 de Chopra
Solución
Al resolver el ejercicio, conviene primeramente explicar las fuerzas que actuan en la masa M del sistema.
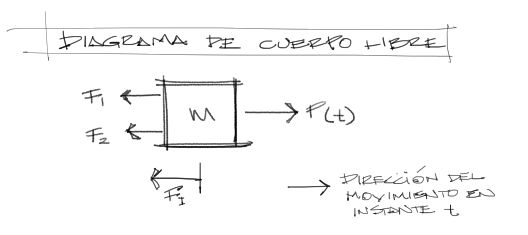
Aplicando el equilibrio dinámico de D’Alembert podemos ver que en la dirección opuesta a la aceleración P(t), actuan:
– La fuerza del resorte k1
– La fuerza del resorte k2
– La fuerza ficticia de inercia en dirección contraria al movimiento FI.
Posteriomente podemos aplicar la ecuación de equilibrio:

Explicamos las cuatro expresiones de la ecuación obtenida:
- FI: Fuerza de inercia (ficticia)
- F1: Fuerza del resorte con rigidez k1
- F2: Fuerza del resorte con rigidez k2
- P(t): fuerza externa desplazando a la masa una magnitud “u” (deformación)
Reemplazando todas las expresiones en la ecuación de movimiento:
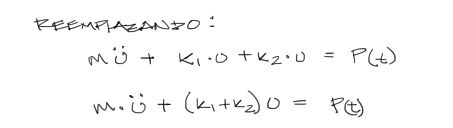
Debido a que los resortes se aplican en paralelo, las fuerzas de ambos resortes se suman. La suma de las fuerzas de los resortes resulta directamente en la suma de las rigideces de sus resortes (k1 + k2).
Consideraciones adicionales
Este modelo matemático es uno de los más sencillos para describir las ecuaciones de movimiento, y le es correspondido un sistema estructural más realista. Este sistema realista está representado a continuación por dos columnas deformables y una viga indeformable e infinitamente rígida. A la vez, la masa se concentra en el centro geométrico de la viga.
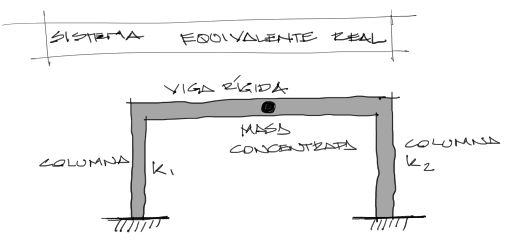
Este sistema es muy común en galpones, casas de una planta y sistemas en general de un solo nivel. La masas puede concebirse concentrada en un solo punto cuando la viga o losa representa un diafragma rígido poco deformable respecto a la deformación de las columnas.
El modelo matemático correspondiente con la dirección del movimiento es:
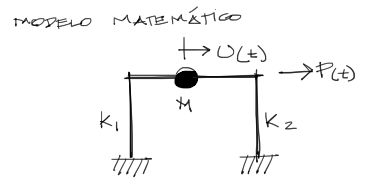
Este sistema de la figura puede describir su movimiento a partir de la ecuaciónd deducida arriba.
autor: Marcelo Pardo