Enunciado
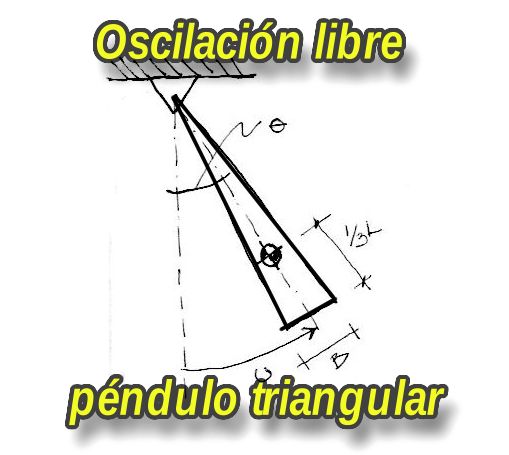
Encontrar la ecuación de movimiento del sistema mostrado en la figura
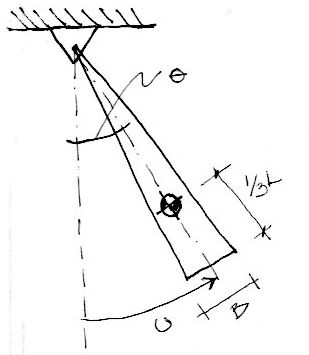
Posteriormente determinar la ecuación para pequeños desplazamientos y encontrar la frecuencia natural del péndulo. La masa del péndulo es “m”
Solución
La masa del péndulo se encuentra ubicada en el centroide del triángulo, o sea, a 2/3*L medidos desde el apoyo, o L/3 desde el extremo.
fuerza inercial
Esta masa genera una fuerza inercial ficticia en el sentido contrario al movimiento. Asumiento movimiento hacia la derecha, la fuerza inercial se dirige hacia la izquierda. Su magnitud será masa por aceleración.

La aceleración rotacional la convertimos en aceleración lineal a partir de arco = radio*ángulo.
fuerza de gravedad
La aceleración de la gravedad genera una fuerza que jala al cuerpo siempre hacia el centro. La componente de esta fuerza que genera ese movimiento es la perpendicular al eje del péndulo. Por tanto:

ecuación de movimiento
La ecuación de movimiento se compone de la suma de todas las fuerzas que actuan en el sistema. En este caso debido a la naturaleza rotacional del sistema, se realiza la suma de momentos respecto al punto de apoyo. por tanto:

Se pueden simplificar términos comunes siempre y cuando se sepa que estos términos son diferentes de cero.
pequeños desplazamientos
Para pequeños desplazamientos, el SIN(ángulo) se confunde con el ángulo en radianes, y por tanto:

reemplazando:
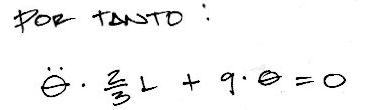
frecuencia natural
La frecuencia natural del sistema se define como la raiz de la razón de la rigidez respecto a la masa. En este caso la rigidez del sistema es el término que acompaña al desplazamiento y la masa el término que acompaña a la aceleración. Por tanto:

autor: Marcelo Pardo