Antecedentes
Si bien esta es una viga isostática y pueden encontrarse sus solicitaciones por método más sencillos, el método aplicado de la elástica permite encontrar además la ecuación de la deflexión de la viga en función a los valores q1 y q2.
Esta resolución posteriormente servirá para la resolución de pórticos con articulaciones por el método de rigidez.
Enunciado
Resolver la viga simplemente apoyada mostrada en la imagen.
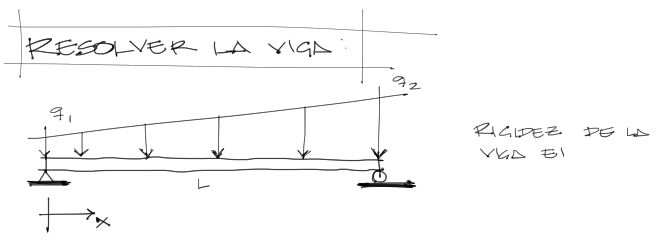
Encontrar los diagramas de cortante, de momento flector, reacciones y deflexión de la viga.
Resolución
La resolución completa y a detalle de la viga puede descargarse del siguiente PDF: Borrador de resolución de viga simplemente apoyada. Método de la elástica.
Ecuación de la elástica
Se adopta el método de la elástica para obtener además las deflexiones de la viga en función de la coordenada “X”
El primer paso de la resolución es conocer la ecuación de la carga en función de “x”. Esta es la ecuación de una recta que pasa por los puntos q1 y q2.

Luego esta ecuación se reemplaza en la ecuación de la elástica.
Integración
Esta ecuación se integra cuatro veces. Las ecuaciones integradas representan respectivamente:
- EI*d3u/dx3: Cortante
- EI*d2u/dx2: Momento flector
- du/dx: Pendiente de deflexión
- u: Deflexión
Realizando la integración, queda:

Condiciones de contorno
Las condiciones de contorno dan un significado físico a las ecuaciones mostraras arriba. Para el presente problema, como en ambos extremos la deflexión y momento flector son cero en los apoyos, se tiene:
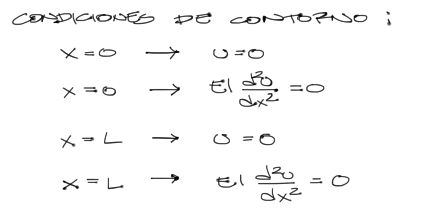
Estas ecuaciones de contorno se deben reemplazar en las integrales de la ecuación de la elástica para encontrar las constantes de integración. Estas constantes son las incógnitas del problema, que una vez encontradas singularizan la solución general obtenida en esas ecuaciones integradas.
Constantes de integración
Reemplazando las condiciones de contorno y operando, se obtiene la solución de las constantes. (La manera más detallada de esta resolución está en el documento borrador cuyo enlace de descarga está arriba).

Ecuación de cortante
Reemplazando la constante C1 en la primera integral de la elástica se obtiene el cortante de la viga.
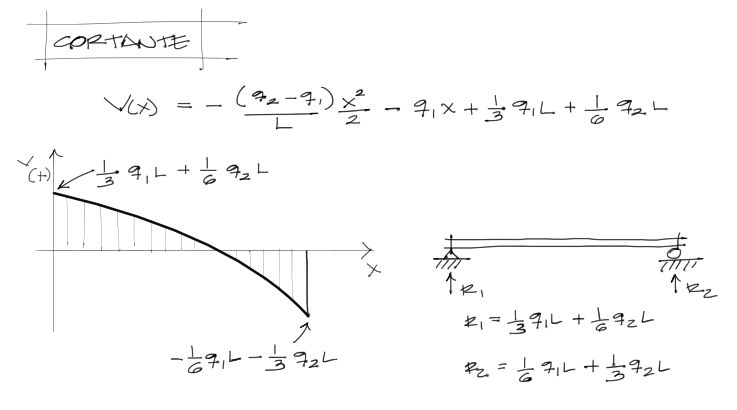
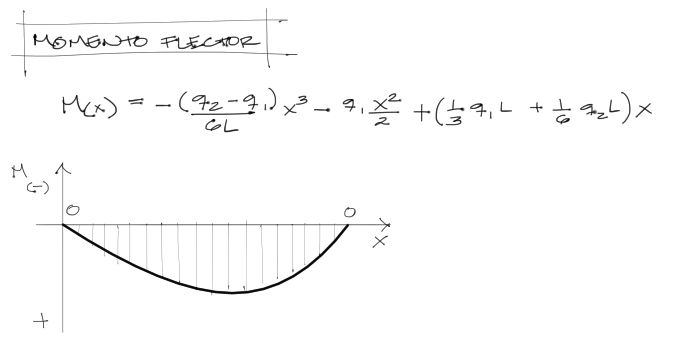
Ecuación de momento flector
Reemplazando las constantes C1 y C2 en la segunda integral de la elástica se obtiene el momento flector de la viga.
Ecuación de deflexión
Reemplazando las 4 constantes de integración en la última ecuación integrada de la elástica se obtiene la ecuación que describe la deflexión de la viga, que en el borrador se comprueba que pasa por cero en ambos extremos de la viga.

autor: Marcelo Pardo