Enunciado

Se resolverá una viga sencilla por el método de integración de la elástica de la viga.

Dada la siguiente viga:

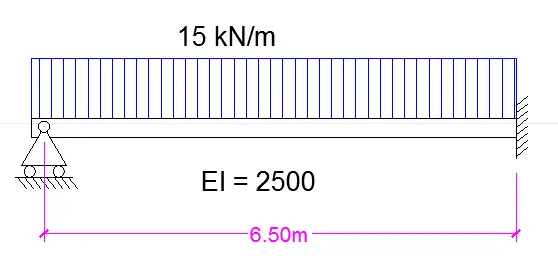
Se debe resolverla por el método de integración de la elástica de la viga

SOLUCIÓN

Las ecuaciones de la elástica de la viga son las mostradas en la teoría y también a continuación. Para verlas a más detalle hacer click en el link de TEORÍA DE RESOLUCIÓN DE VIGAS POR MÉTODO DE LA ELÁSTICA.

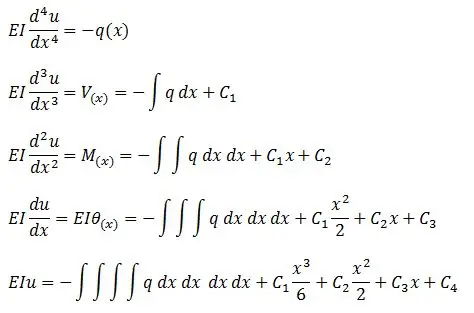
La variable “q(x)” representa la carga distribuida en la viga. Como la carga distribuida es constante de extremo a extremo y los apoyos también se encuentran en los extremos, sólo se usarán estas ecuaciones de la elástica una vez. OJO: Si existieran diferentes tipos de cargas distribuidas o apoyos intermedios, deberá utilizarse la ecuación de la elástica en cada tramo. A futuro se publicará otro ejercicio más complejo mostrando este segundo caso.

Volviendo al presente ejercicio, todos los datos para las cuatro ecuaciones mostradas son:

• q(x) = 15
• EI = 2500 KN-m2

Las constantes C1, C2, C3 y C4 son las que se deben determinar.

Para ello contamos con las condiciones de borde siguientes:

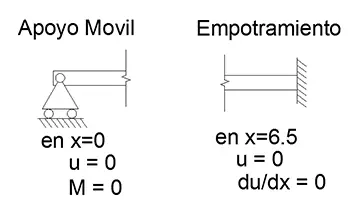
Para x=0, contamos con las condiciones de borde u=0 y M = d2u/dx2=0, por tanto debemos reemplazarlas en las ecuaciones 4 y 2 de la elástica.

Para x= 6.5[m] contamos con las condiciones de borde u=0 y du/dx = 0 que se deberán reemplazar en las ecuaciones 4 y 3 respectivamente.

Reemplazando todos estos datos, tenemos entonces:

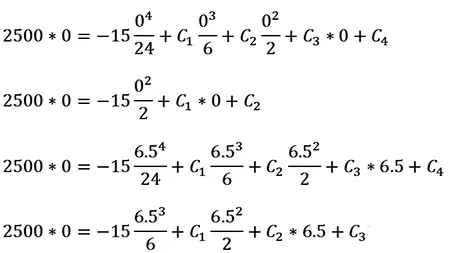
Reordenando los datos y escribiéndolos en forma matricial, tenemos:

Y resolviendo el sistema de ecuaciones, resulta:

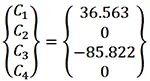
Con estas constantes encontradas ya se tienen todos los datos para la graficación de cortante, momento flector, pendiente de deflexión y deflexión de la viga. Solamente se deben reemplazar las constantes en las ecuaciones de la elástica y graficarlas.

Entonces, se tiene:

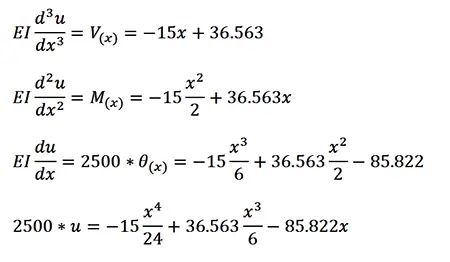
Y graficando estas ecuaciones

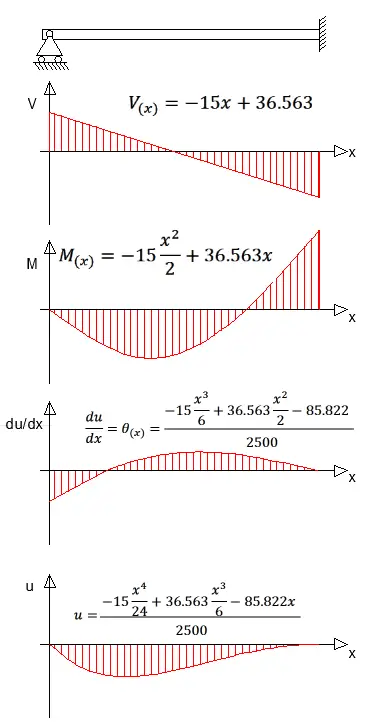
Nota que en las dos últimas ecuaciones se despejó la pendiente «du/dx» y la deflexión «u» del valor de 2500. Este paso es escencial para conocer los valores de pendiente y deflexión reales.

Con esto termina el ejercicio.

Si tienes dudas, las puedes escribir justo abajo de esta publicación