
El problema
En la portada se ve una losa que a la vista tiene un espesor demasiado bajo para la luz que cubre. Esta deflexión excesiva puede deberse principalmente a dos factores:
– Desencofrado temprano
– Espesor muy pequeño en losa para soportar las cargas de diseño

Es bien sabido que en estructuras de concreto, metal o madera, se deben hacer verificaciones tanto a las Resistencias como a las Deflexiones. Muchas veces se realiza solo la primera verificación dejando de lado la verificación a deflexiones cuando son igual de importantes que las primeras.
Medidas del pórtico
Para estimar las dimensiones del pórtico de la fotografía se debe realizar un trabajo de escalado en un programa de CAD. Tengo un tutorial completo de como escalar una imagen fotográfica para poder de ésta, tomar sus medidas. Ese enlace está a continuación:
Te recomiendo ver ese video por unos minutos
Básicamente en el video explico que primero se debe importar la fotografía a analizar a Autocad o Nanocad. La imagen importada estará sin escalas.
Luego se debe buscar una distancia conocida dentro de la imagen, que se pueda asumir como correcta. En la mayoría de los casos la distancia de piso a piso suele ser conocida o bien estimada. Esa distancia acá la estimaremos de 2.7m. Entonces se escala toda la imagen de tal forma que la altura de piso a losa sea de 2.7m. A partir de esa imagen escalada, ya se pueden hacer las demás estimaciones de medida.
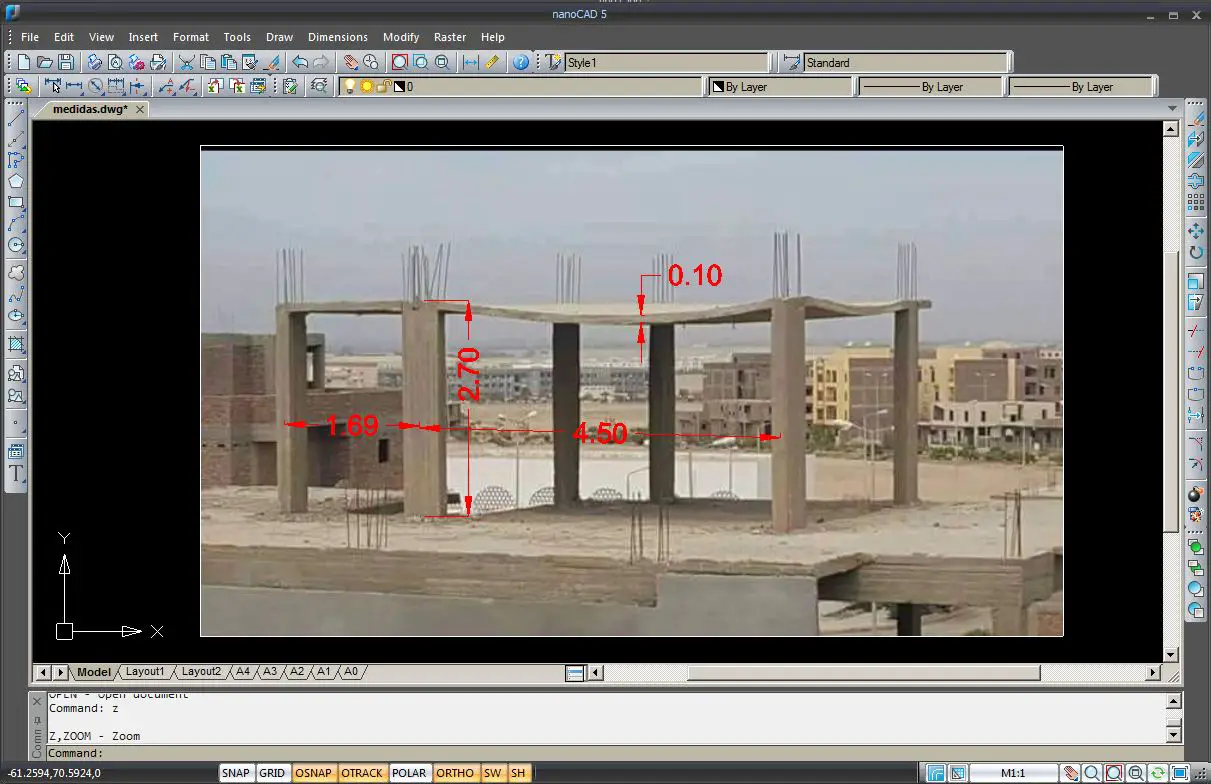
Si bien se incurre en error, este no deberá ser significativo, especialmente para todas las medidas que se encuentren en la profundidad de la primera medida asumida. Algo más difícil de estimar es la medida de profundidad entre columnas. Para fines pedagógicos se asumirá una distancia de 3.5m

Espesor mínimo
La losa a estudiar tendrá la siguiente forma en planta:
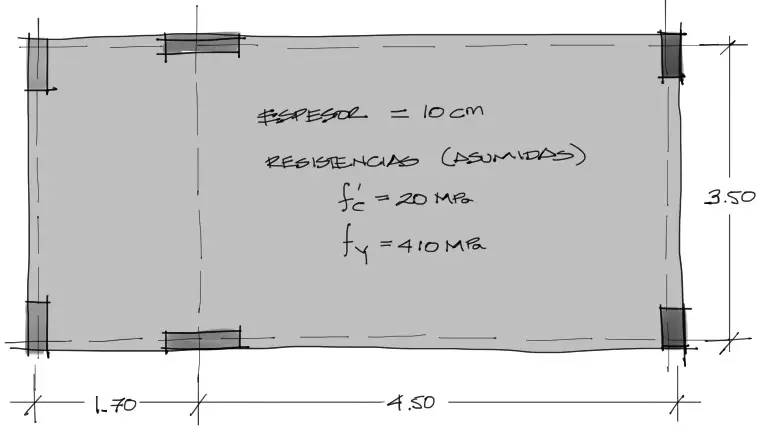
Asumiremos las resistencias tanto de acero como de concreto. Las resistencias asumidas son las mínimas que podrían utilizarse en obra.
Según la normativa ACI en la tabla 8.3.1.1 se indican espesores mínimos de losas en función a la luz más larga que cubren los cuadrantes entre columnas.
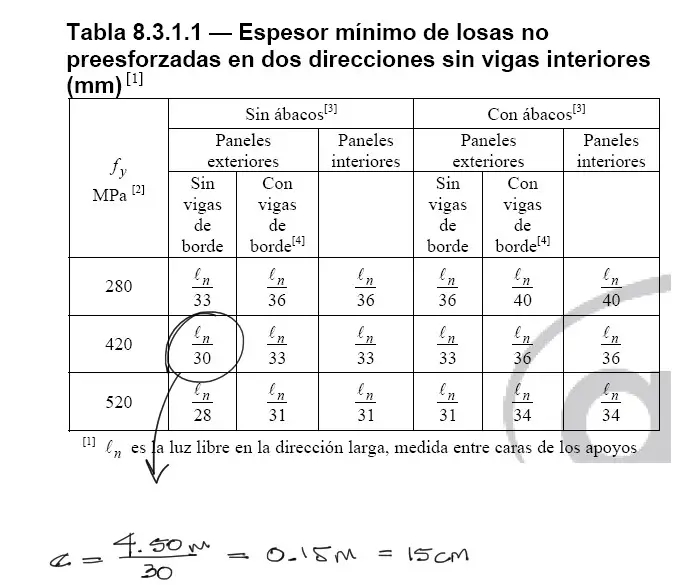
La tabla tiene varias opciones. Para empezar debemos identificar si nuestra losa de estudio tiene ábacos o no. Una losa con ábacos o con capiteles llevará un recrecido en la zona de apoyo con las columnas. Este ábaco ayuda a transferir mucho mejor los esfuerzos de flexión y principalmente de cortante desde la losa hacia la columna.
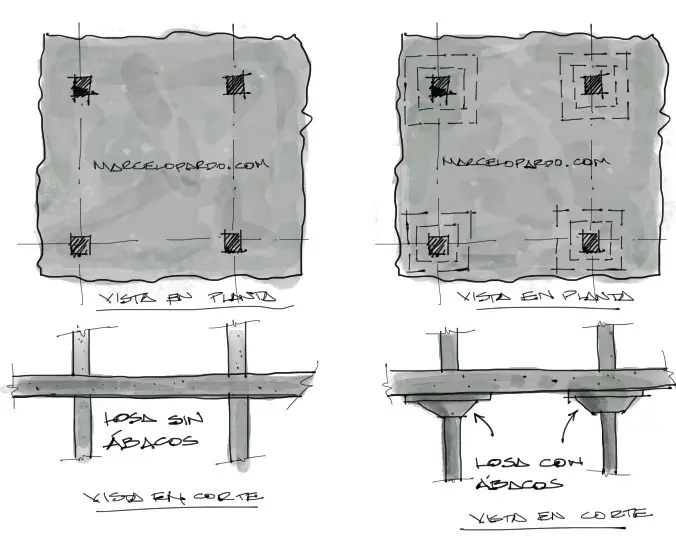
Por otro lado el panel que estamos estudiando es un panel exterior ya que el cuadrante entre las 4 columnas coincide en los bordes con el perímetro de la losa. De hecho cada uno de los cuadrantes tiene tres lados de borde. Finalmente el acero asumido a utilizar será de 410 MPa (uno de los aceros de resistencia más común en el mercado).
Para todos estos parámetros, el espesor de la losa en función a la luz más larga es de L/30. Para nuestro caso el cálculo resulta en una losa de 15cm de espesor.
Análisis de solicitaciones de flexión
El método que utilizaremos para la deducción de solicitaciones es el mencionado método directo que es sugerido en la norma ACI 318-14 en su artículo 8.10. Si bien hay restricciones que en este caso no se cumplen para aplicar el método, al menos a partir de su aplicación obtendremos resultados que se aproximan a los reales en una magnitud tal que nos permita realizar un diseño a mano de la cantidad de acero.
Para aplicar este método se debe dividir el pórtico en franjas en ambas direcciones. Cada división se realiza entre centros de columnas. Luego se analiza cada franja como una viga plana apoyada en las columnas.
Análisis de franjas horizontales
Se realiza la división imaginaria de las franjas horizontales. En este caso por simetría solo debemos analizar una franja de 1.75m de ancho como se muestra en la figura:
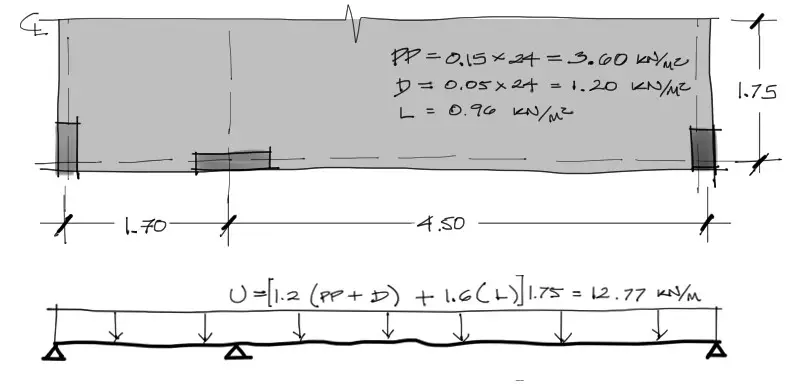
Luego se debe cargar la “viga plana” con las cargas de uso mayoradas y linealizadas:
– Peso Propio PP: espesor de losa x peso específico (24 KN/m3)
– Carga muerta D: compuesta por revoques y recubrimientos equivalentes a 5cm de carpeta de mortero
– Carga viva L: Según la ASCE 7-16, en su tabla 4.3-1 la carga mínima viva para techos es de 0.96 KN/m2
Una vez calculadas las cargas, se deben mayorar. Las cargas muerta y peso propio por 1.2 y la carga viva por 1.6. Además la linealización de la carga para calcular q en KN/m se realiza multiplicando todas las cargas por el espesor de la franja: 1.75m.
Si bien se puede modelar la franja como un pórtico compuesto por vigas y columnas, es mejor asumir un modelo de vigas apoyadas en apoyos articulados. Esto es conveniente para despreciar la rigidez de las columnas en los extremos. Esto transfiere los momentos negativos de la viga en los extremos hacia los positivos en los tramos positivos. De esta manera no se generan momentos en las columnas externas y por tanto no existe transferencia de momento por excentricidad de cortante.
Calculando entonces las solicitaciones de la losa en dirección horizontal:
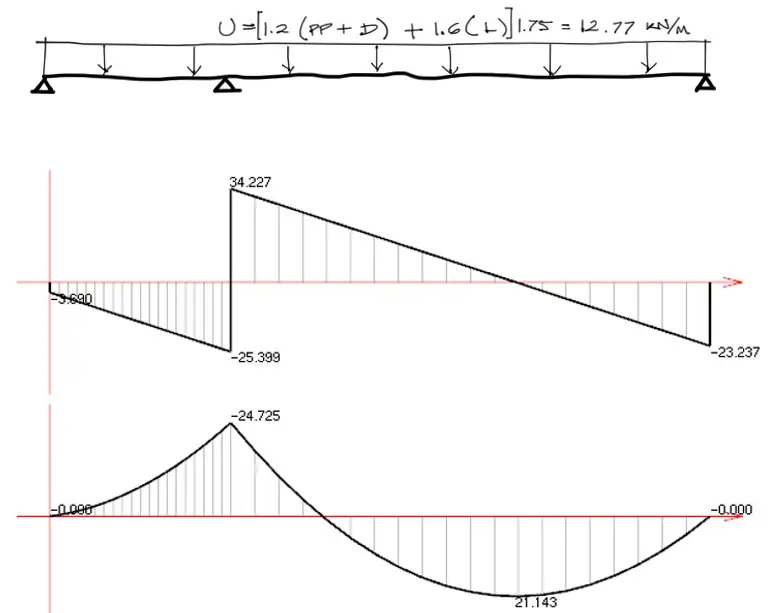
Refuerzo horizontal
Una vez calculadas las solicitaciones de momento, se debe repartir este momento flector dentro de las llamadas FRANJA DE COLUMNA y FRANJA CENTRAL para la sección de losa analizada. Una franja de columna tiene un ancho del 25% del ancho total analizado medido desde el eje de columnas hacia cada lado del eje. La franja central es el ancho restante. Para nuestro caso se tiene:
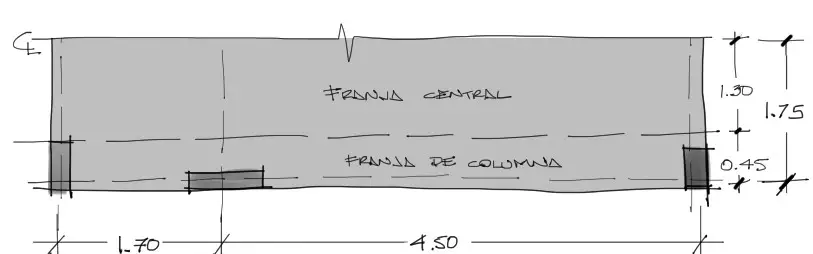
Los momentos calculados en el diagrama de momentos flectores arriba, se debe redistribuir entre la franja de columna y la franja central a partir de los siguientes porcentajes:
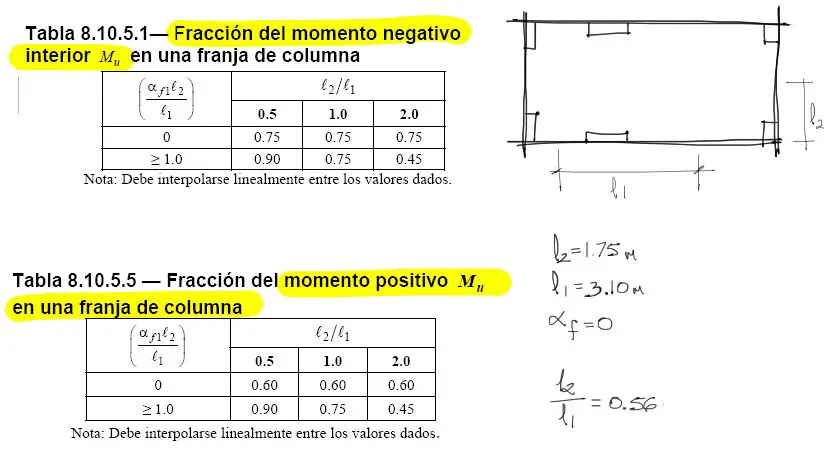
Las tablas mostradas indican el porcentaje de momento que absorbe la franja de columna, según los parámetros de las tablas. (Estas tablas fueron extraidas de la norma ACI 318-14).
La relación l2/l1 es la relación de longitudes centro a centro entre columnas en direcciones perpendicular y longitudinal al análisis, respectivamente. αf corresponde a la relación entre rigidez de viga respecto la rigidez de la losa en la dirección del análisis. Como en nuestro caso no existe viga en la losa, αf es igual a cero. Por tanto para l2/l1 = 0.50 aproximadamente, y para losa sin vigas, en los momentos negativos, 75% del momento negativo debe aborberse por la franja de columna y el restante en la franja central. Además 60% del momento positivo debe abosorberse por la franja de columna y 40% por la franja central.
Aplicando estas directrices se tiene:
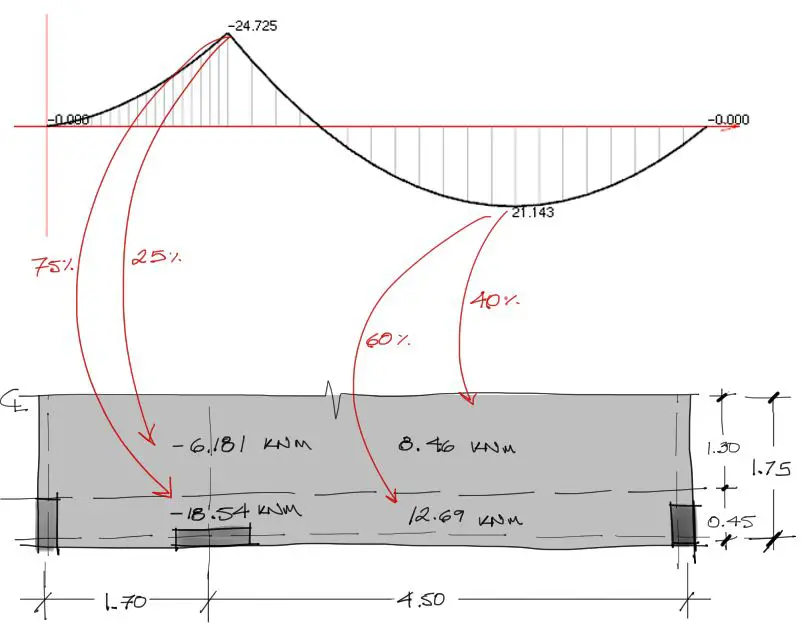
Los momentos distribuidos en las franjas se deben convertir en sección de acero para la zona traccionada de la losa. Esto podemos lograrlo a partir de la teoría de refuerzo a flexión de losas o directamente utilizando un programa de cálculo de diseño a flexión de losas.
Por ejemplo para la solicitación de 18.54 KNm que nos tracciona la zona superior de la losa, introducimos los datos al programa:
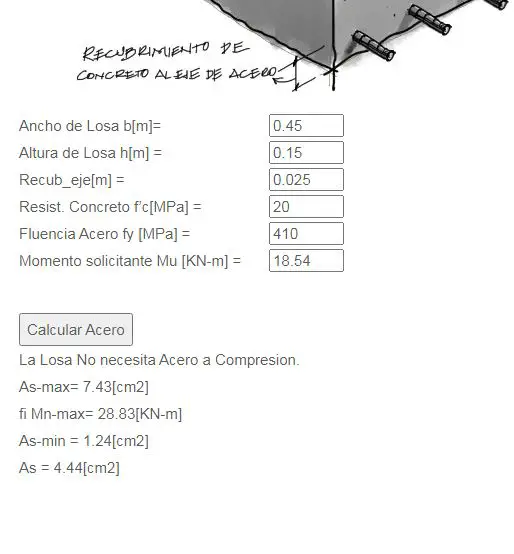
Y el programa nos devuelve una sección de acero de 4.44cm2 que debemos convertir en acero:

Este procedimiento se repite para todos lo momentos obtenidos y se distribuye el acero según el siguiente croquis:
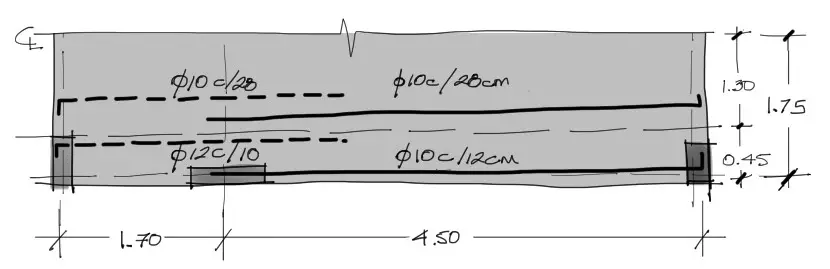
Refuerzo en dirección vertical
En la dirección vertical se procede de la misma manera dividiendo franjas entre centros de columnas, con la ventaja de que en este caso solo tenemos momentos positivos de tramos simplemente apoyados.
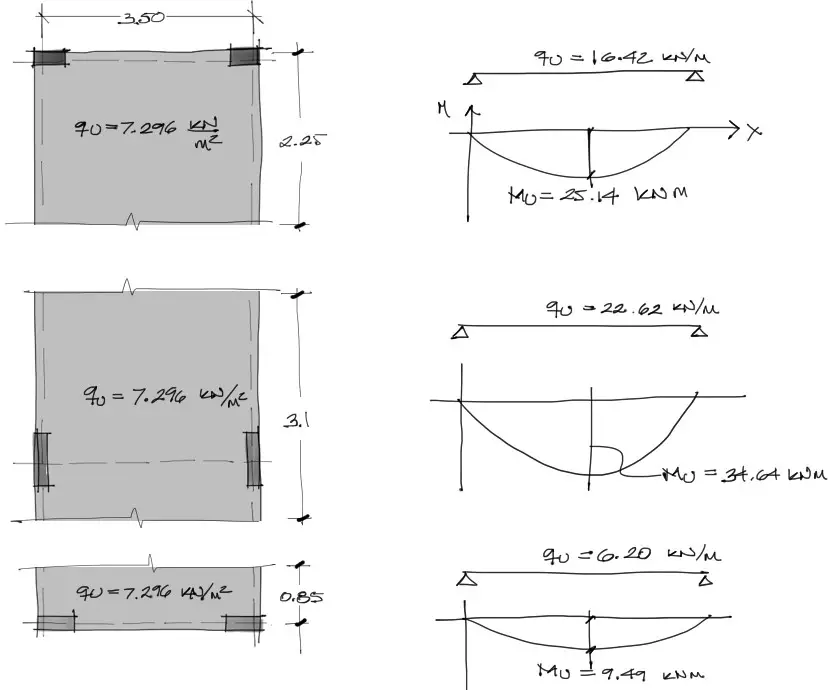
Al igual que en el caso anterior, se divide el momento flector en franjas de columna franjas centrales, con la salvedad de que como en la zona inferior se tienen distancias muy cortas entre columnas, se hizo una división de franja de columna y franja central más a criterio. En defecto, ya dijimos que no se cumplian todas las cláusulas de la aplicación de este método para el refuerzo de losas, por tanto aqui estamos haciendo un cálculo de acero rápido que debería coincidir con el diseño de acero por métodos más sofisticados.
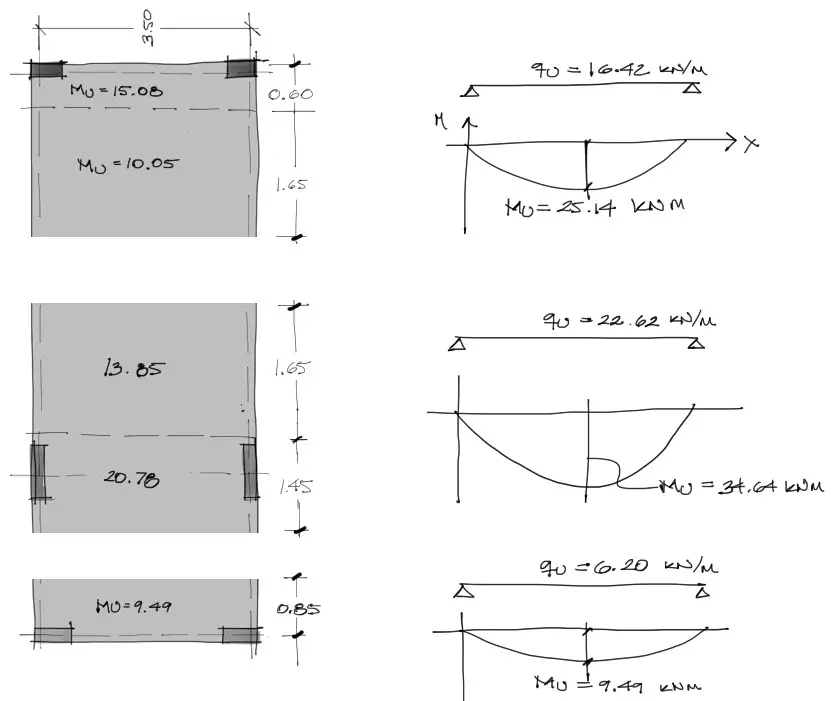
Repitiendo el proceso ya explicado antes, distribuimos el acero con la ayuda del programa de flexión de losas y el razonamiento de conversión de sección de acero a espaciamiento entre barras, esta vez de 10mm:
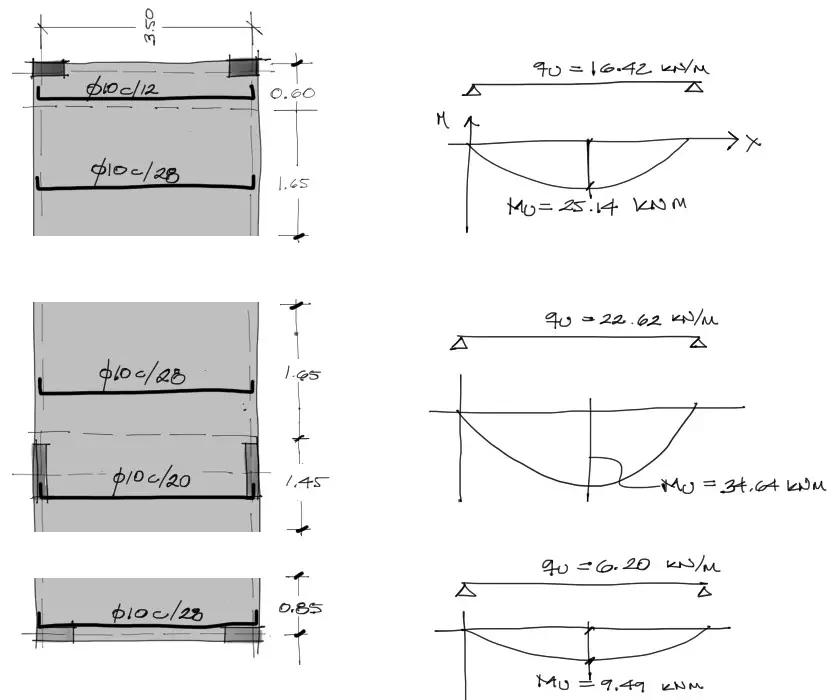
Nota importante
En losas llenas o macizas no es necesario que exista acero inferior y superior en todas las zonas de la losa. Esto solo es necesario para losas de espesor mayor a 30 cm. Para losas de menor espesor a 30cm se debe satisfacer el acero mínimo por retracción y fraguado (que ya fue calculado en el programa) que puede ser colocado solo en una cara de la losa.
Verificación a cortante
La verificación a cortante por punzonamiento debe hacerse para todas las interesecciónes entre columna y losa, sin embargo nos iremos al caso más desfavorable de la esquina derecha superior e inferior de la losa vista en planta. Esta esquina es la más desfavorable ya que el esfuerzo de punzonamiento entre losa y columna se distribuye sobre una superficie de contacto muy pequeña y por tanto el esfuerzo en esta zona será relativamente alto respecto a las otras columnas.
Asumiremos columnas de 20×30 por simplicidad. A pesar de que todas las columnas parecen de una dimensión mayor a 20x30cm de sección, veremos que incluso esta sección pequeña cumple con el punzonamiento, y por tanto cualquier columna de mayor sección también lo hará.
Esfuerzo solicitante
Para encontrar el esfuerzo de cortante en la conexión de columna con losa, primero debemos conocer la reacción de la columna hacia la carga de la losa en Estado Límite Último. Esto es sencillo analizando la viga simplemente apoyada correspondiente a este apoyo del análisis a flexión:
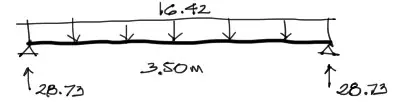
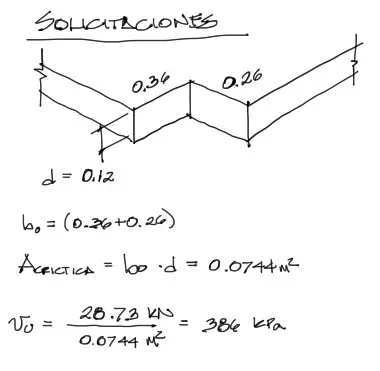
Luego, la sección crítica por la cual los esfuerzos de cortante son más altos, es a una distancia d/2 de la cara de la columna.
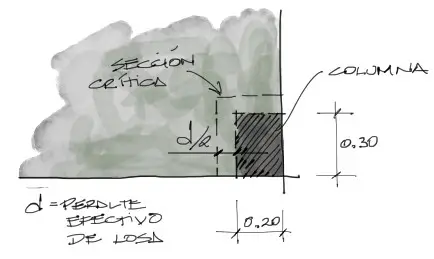
La superficie crítica Acrítico se encuentra a partir de este perímetro crítico bo multiplicado por la altura efectiva de la losa. Y finalmente el esfuerzo solicitante en el contacto entre losa y columna es la división entre la fuerza cortante y el área crítica.
Esfuerzos resistentes de la unión
La resistencia a punzonamiento de la unión de losa a columna se define a partir de tres fórmulas propuestas por la norma ACI318.

Los parámetros de estás 3 fórmulas son:
– f’c: Resistencia a compresión del concreto en MPa
– β: relación del lado largo / lado corto de columna
– αs : 20 para columnas de esquina; 30 para columnas de borde; 40 para columnas centrales
– bo : perímetro crítico (explicado arriba)
– λ: 0.7 para concreto liviano; 1.0 para concreto de densidad normal
– d: peralte efectivo de la losa
Reemplazando todos los datos en las fórmulas, obtenemos las siguientes resistencias de esfuerzo, de las cuales adoptamos la menor:
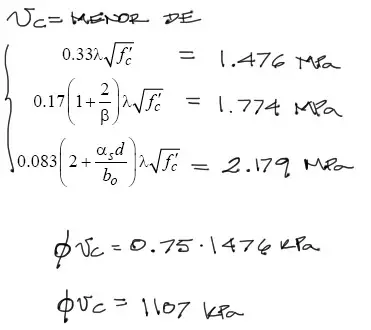
Este esfuerzo vc resistente se debe multiplicar por un factor de seguridad ø=0.75, y el valor obtenido es el esfuerzo de diseño proporcionado por el concreto que debe ser menor al esfuerzo solicitante. En este caso las resistencias SI son mayores a las solicitaciones por tanto la losa resiste a cortante para las cargas de diseño.
En caso de que el cortante resistente de diseño øvc fuera menor que vu, se debe solucionar el problema con una de las 4 alternativas:
– Incrementar altura de la losa
– Incrementar sección de las columnas
– Aumentar ábacos o capiteles a la losa en la zona de columnas
– Reforzar la losa con refuerzo a cortante en la zona crítica
La más práctica de todas ellas es incrementar la sección de columnas o sección de losa.
Fin de los cálculos
Se encontraron hasta aquí todos los elementos necesarios para la construcción de la estructura sin complicaciones de deflexión.
autor: Marcelo Pardo
![Lee más sobre el artículo Diámetros de acero. Diferencias entre acero en [mm] y [pulg]](https://marcelopardo.com/wp-content/uploads/ingenieria_civil/hormigon/acero/diametros_de_acero/00_featured-300x261.png)