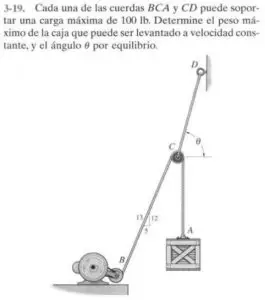
Enunciado

El autor pide resolver la dirección y componentes del vector de fuerza mostrado

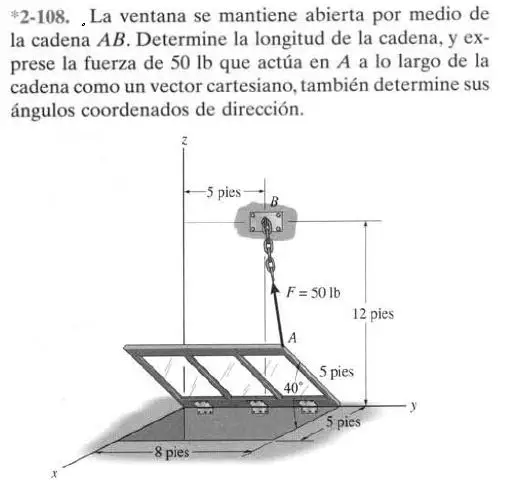
Solución

Vectores posición de A y B

Primero debemos encontrar los vectores posición de A y B, o lo que es lo mismo, las coordenadas cartesianas de estos vectores. Para eso debemos descomponer la geometría de la fuerza como se muestra en el gráfico

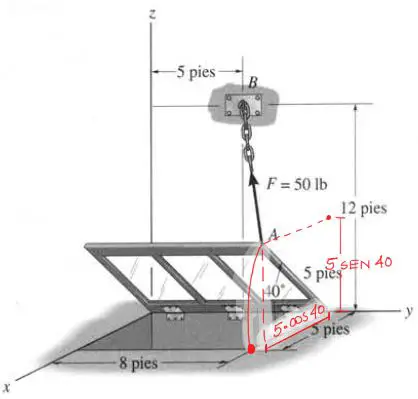
Analíticamente:

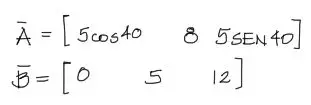
Vector AB

Debemos obtener un vector que apunte en la misma dirección que el vector de fuerza. Este vector es el vector que va desde A hacia B.

El vector AB es la resta del vector posición B menos vector posición A. Restando sus componentes:

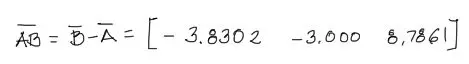
Módulo de AB y Vector unitario AB

Para obtener el vector unitario AB que apunte en la misma dirección que el vector de fuerza, se debe dividir el vector AB entre su módulo.

El módulo de AB es la raiz de la suma de los cuadrados de sus componentes:

Y el vector unitario Uab es AB/|AB|:

Componentes del vector FUERZA

Se tiene como dato, el módulo del vector fuerza, y ya sabemos que Uab apunta en la misma dirección que el vector fuerza, por tanto las componentes de F serán iguales a |F|·Uab donde analíticamente se tiene:

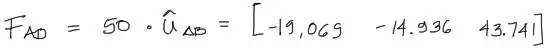
Dirección del vector FUERZA

Las componentes del vector unitario AB son los cosenos directores de este vector. Si despejamos los ángulos de estos cosenos se tiene:

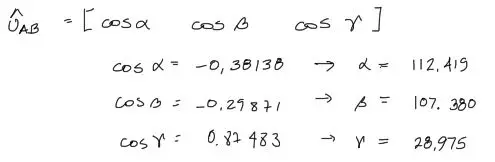
Con eso se termina el ejercicio

← ← ← VOLVER A TABLA DE CONTENIDO DE ANÁLISIS ESTRUCTURAL← ← ←

autor: Marcelo Pardo