Enunciado
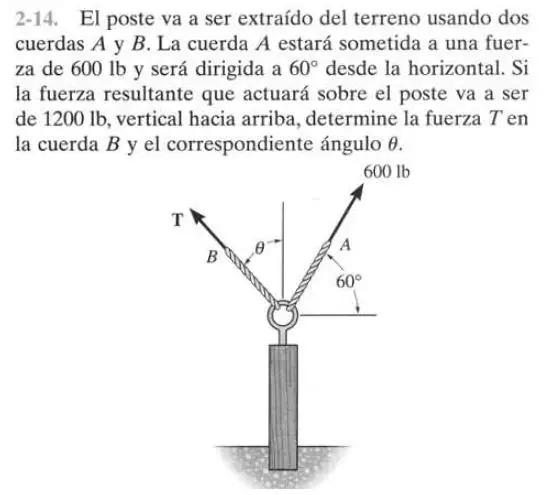
Solución
Primero se deben descomponer los vectores de las dos cuerdas. El vector resultante es el mostrado en verde.
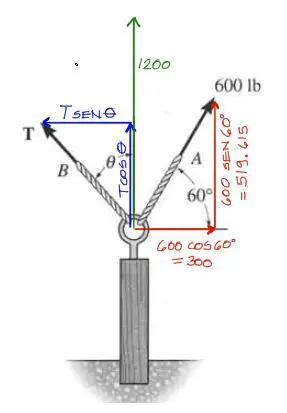
Luego escribimos los tres vectores en función a sus componentes:
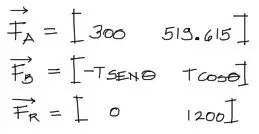
Ahora se deben sumar los vectores Fa y Fb, e igualar al vector resultante Fr. Luego se reordenan los términos.

Para resolver este sistema, dividimos las dos ecuaciones, y de esta manera se simplifica T
La división entre Seno y Coseno genera la función Tangente:

Finalmente se reemplaza el resultado del ángulo en cualquiera de las dos ecuaciones I o II. Escogemos la I.

Con esto termina el ejercicio.
Vídeo
La solución explicada en vídeo a continuación:


EXCELENTE MATERIAL
gracias Oscar!!!!