Concepto

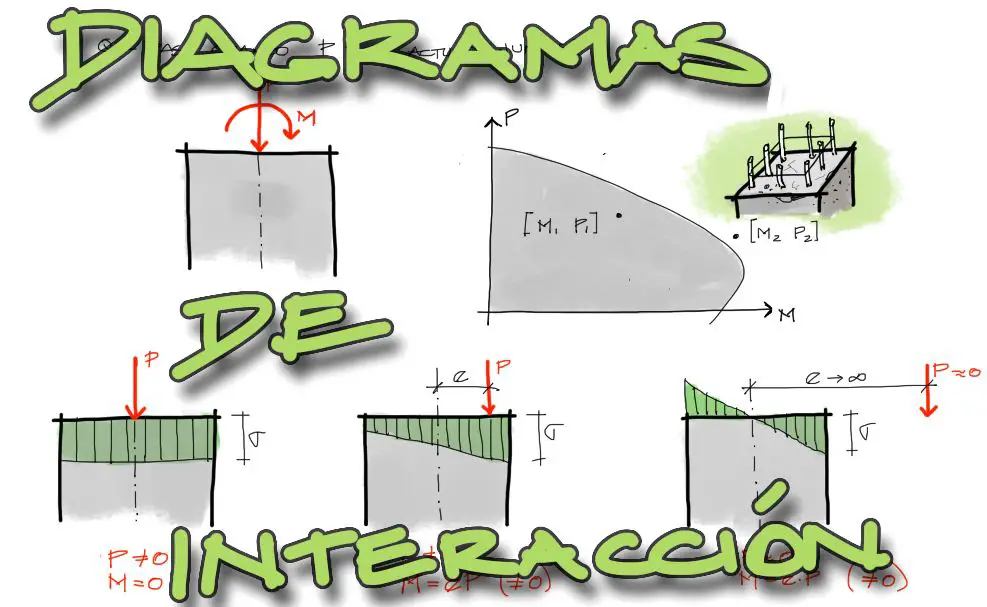
El concepto de diagramas de interacción es ampliamente utilizado en hormigón armado para mostrar de forma gráfica la capacidad resistente de una columna. Estos diagramas se ven más o menos como en la siguiente figura:

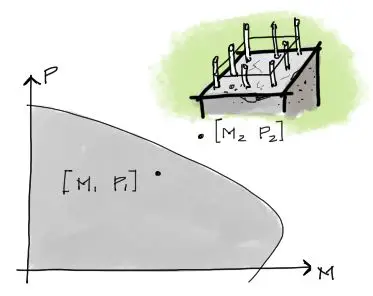
Lo que no está claro en la mayoría de las personas que recién aprende este concepto es la manera de obtener estos diagramas y qué significan exactamente.

En pocas palabras, el diagrama de interacción arriba mostrado indica en un sombreado plomo todo el sector que la sección analizada (una columna por ejemplo) puede resistir en una combinación de esfuerzos entre compresión y momento flector.

Partiendo de lo más sencillo

Fuerza axial admisible

Para entender de mejor manera lo que es un diagrama de interacción, empezaremos por un caso más sencillo de analizar que es el típico caso de compresión simple de una columna. Cuando se aplica una fuerza P de compresión, la sección sufre un esfuerzo interno igual a la fueza sobre el área, como se muestra en la figura.

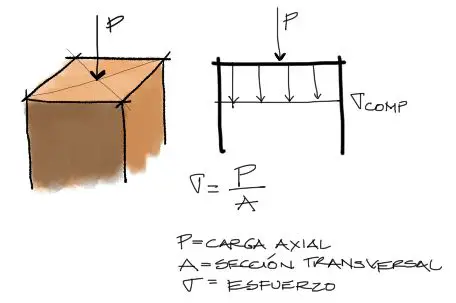
Sabemos que la resistencia del material es limitada, y que esta resistencia se mide también en unidades de esfuerzo. Este límite podemos llamarlo Esfuerzo admisible del material, σ_adm. Por tanto, los esfuerzos σ generados por la fuerza P deben ser menores o iguales a σ_adm para que el material no falle. Gráficamente podemos expresar este último concepto en un diagrama unidimensional como una regla:

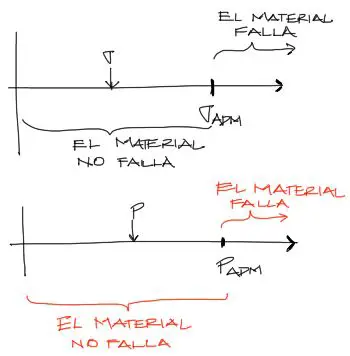
Este diagrama puede expresarse tanto en términos de esfuerzo como en términos de fuerza sin problema.

Momento flector admisible

De la misma manera que con el esfuerzo axial, podemos obtener una relación parecida para los momentos flectores de una pieza.

Los momentos flectores como bien sabemos, generan esfuerzos axiales de tracción y compresión en la pieza analizada, de la siguiente manera:

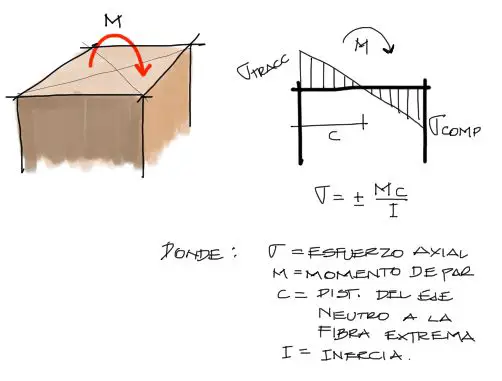
Se utiliza una pieza rectangular en esta figura de ejemplo por simplicidad.

El momento M al generar esfuerzos axiales en la pieza, el momento M podrá incrementarse solamente hasta un punto que los esfuerzos axiales admisibles del material lo permitan (σ_adm). Entonces si despejamos M de la fórmula y reemplazamos σ con σ_adm, se tiene:

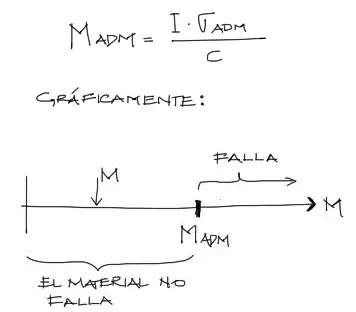
Al igual que con los esfuerzos axiales puede expresarse gráficamente la situación entre el momento solicitante M y su respectivo momento límita M_adm. Si M sobrepasa M_adm el material falla. Por simplicidad en el cálculo anterior se omite el doble signo y se trabaja solamente en valor absoluto.

Ejemplo

En este ejemplo partiremos de los conceptos repasados arriba y extenderemos dentro del mismo ejemplo el concepto de diagrama de interacción para que se comprenda más fácilmente.

Se da una pequeña pieza metálica con la sección transversal de medidas mostradas a continuación. El esfuerzo axial resistente admisible de la pieza es de 250 MPa. Se pide determina cual es la carga P_adm y M_adm (resistentes) que puede soportar la pieza.

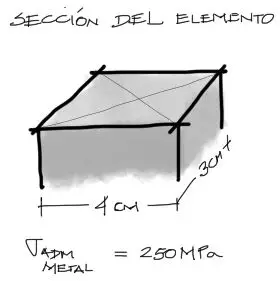
Carga axial admisible

Aplicamos los conceptos ya estudiados, y con un sencillo cálculo encontramos P-adm

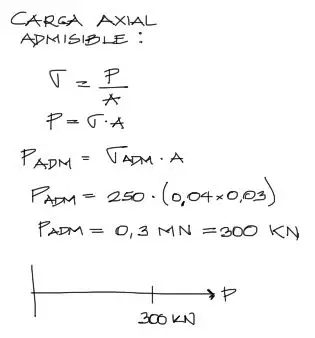
El resultado se obtiene en MegaNewtons, pero a la transformacion a KN vemos que la pieza nos resiste 300 KN a fuerza axial pura.

Momento flector Admisible

Con las fórmulas de flexión ya repasadas arriba, el momento admisible se calcula con la simple aplicación de la fórmula:

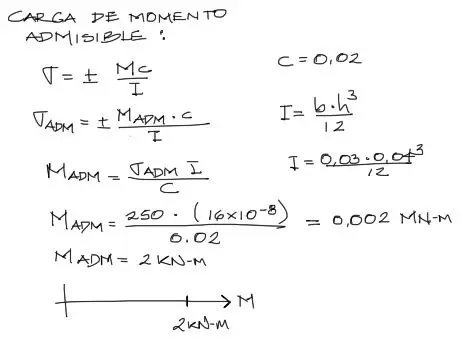
Vemos como en los reemplazos, la pieza soporta un momento flector puro de 2KN-m. Si M sobrepasa los 2 KN-m la pieza fallará.

Combinación de P y M

La pregunta natural a partir del ejemplo anterior surge cuando intentamos cargar la pieza con una combinación de ambas fuerzas.

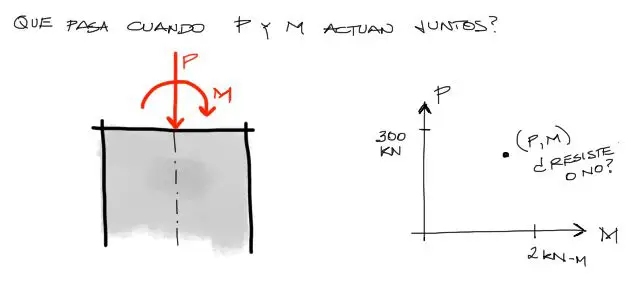
Para eso, podemos aplicar las fórmulas de resistencia de materiales pero además podemos dibujar un diagrama en 2 direcciones con los ejes de fuerzas axiales P y momentos M contrapuestos a 90° como a la derecha del gráfico arriba.

Por tanto, si aplicamos una combinación de P y M a la pieza (columna) este par ordenado [P,M] ocupará un lugar en el plano cartesiano creado. Conocemos además en el plano cartesiano que a fuerzas axiales sin momento flector la pieza resiste 300 KN y a momento flector sin axial la pieza resiste 2KN-m. Esos valores también los tenemos graficados. La pregunta es que sucede en la transición. Para eso necesitamos una frontera en el plano cartesiano para saber si P y M aplicados a la pieza son o no son resistidos por σ_adm.

Dibujo del diagrama de interacción

Para poder dibujar el diagrama de interacción necesitamos manejar las fórmulas que relacionan esfuerzos con fuerzas en base a la menor cantidad de parámetros posible. Para eso, podemos expresar el momento flector M aplicado como una combinación de fuerza «P» y brazo «e». Cuando e=0, el momento es cero, y cuando queremos aplicar una combinación de momento flector y axial a la pieza, podemos expresar a M = e·P. En el caso extremo donde querramos momento flector sin compresión axial en la pieza, elevamos «e» a valores muy grandes y reducimos P a valores cercanos a cero. De esa manera obtenemos un momento casi puro.

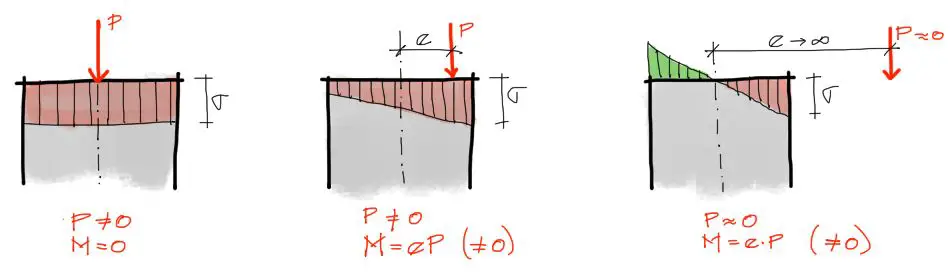
En las tres situaciones mostradas para P en compresión, el esfuerzo de compresión a la derecha dentro de la pieza es el más desfavorable y el que llegará antes a σ_adm, por tanto es este lado del esfuerzo de la pieza el que se analizará.

De resistencia de materiales sabemos que podemos combinar esfuerzos axiales y de momento flector sumándolos como en la fórmula siguiente (si se analizara el esfuerzo en el lado izquierdo de la pieza, los esfuerzo se restarían, pero el lado izquierdo no corresponde al caso crítico):

Como expliqué antes, la fórmula arriba se puede manejar en función a los parámetros P y e, y anular el momento flector de las ecuaciones. Por otro lado reemplazamos σ por σ_adm. De estos reemplazos, podemos conocer el valor de P que logra el esfuerzo límite σ_adm. Para esto despejamos P.

Se genera un sistema de dos ecuaciones con un parámetro variable que es la excentricidad «e». Esto quiere decir que si variamos «e» desde valores de 0 hasta valores muy grandes, tendremos toda la gama de resistencias [M,P] que conformarán la frontera de resistencia de nuestra pieza, y ese es precisamente el diagrama de interacción de la pieza.

Variando entonces e, y encontrando P y M para estas variaciones de «e», se tiene:

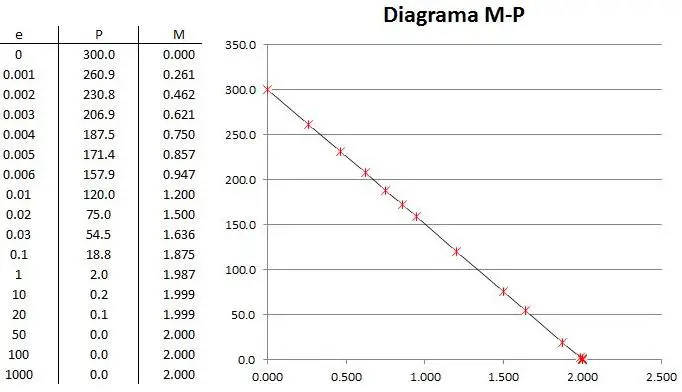
La forma de interpretar el anterior diagrama va como sigue. Si se tiene una solicitación de momento flector y axial [M,P] dibujado sobre la gráfica arriba, si el par ordenado cae dentro del triángulo sombreado, la pieza no falla. Si pasa lo contrario la pieza está esforzada por encima de su resistencia.

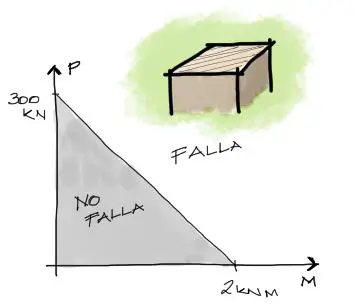Si bien este diagrama solo está dibujado para fuerzas P de compresión y un momento en la dirección analizada, se puede completar el diagrama para los otros 3 cuadrantes del plano cartesiando.

Diagrama de interacción del hormigón armado

Para piezas de hormigón armado, el análisis es un poco más complejo, pero se mantienen los mismos principios de análisis aquí mencionados. Sin embargo al tratarse el hormigón de un material heterogeneo y que además se analiza en estado plástico, el análisis llevará otros conceptos de diagramas de compatibilidad de deformaciones que se analizará en un próximo artículo.

Por el momento es suficiente mencionar que realizando un análisis análogo a la pieza homogenea analizada en el ejemplo arriba, para el hormigón se obtendrá un diagrama de interación de la forma siguiente:

A este diagrama todavía se le deben aplicar factores de seguridad que se explicarán a todo detalle más adelante.

Video

El mismo contenido en forma de vídeo lo puedes encontrar en:

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE HORMIGÓN ARMADO←←←