Comentarios Iniciales
En viviendas modernas y minimalistas está muy de moda el generar sombra o arquitectura estética a partir de losas voladas con grandes luces y siempre surge la incógnita de cuánto es el voladizo máximo que se le puede dar a una losa para dimensiones típicas de vivienda.
En verdad esta es una incógnita que no puede ser respondida de manera muy directa pues cada voladizo es distinto, y se trata de manera diferente.
En ese sentido, en esta publicación veremos la manera de abordar cada tipo de voladizo en particular para la resolución estructural del mismo.
Voladizos de viguetas en una dirección
Es el tipo más común y sencillo de construir y también de calcular. Consiste en volar la losa a partir de un apoyo de viga, donde la losa compuesta por viguetas vuela en dirección perpendicular al apoyo (la viga).
La longitud prudente a volar con este tipo de voladizo es de aproximadamente 1[m] para viguetas de 20cm de altura. Sin embargo estas magnitudes son solo cualitativas.
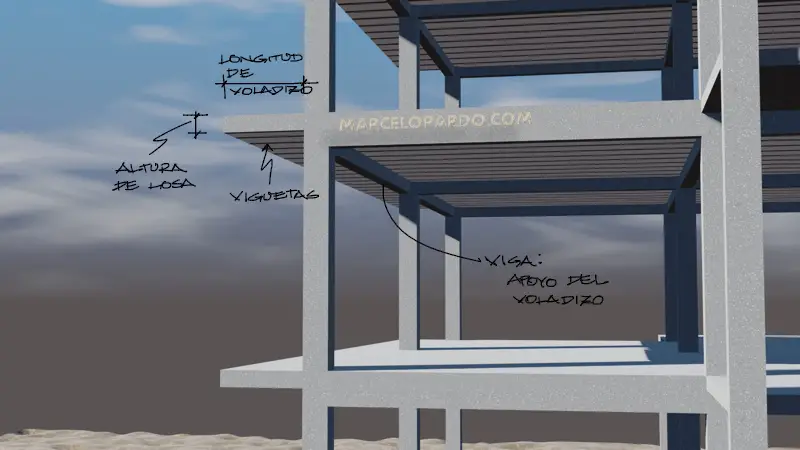El factor crítico en este tipo de voladizos consiste en que las cargas más fuertes de tabique se acomodan en la realidad al borde del voladizo, mientras que muchas veces el calculista considera las cargas distribuidas uniformemente a lo largo de la longitud del volado, y eso puede llevar a una subestimación de las deflexiones.
Una de las ventajas de este tipo de voladizos es que es bastante seguro ante sobrecargas, pues si una de las viguetas estuviera sobrecargada, siempre existirán las adyacentes que ayuden a repartir al carga.
El modelo matemático que rige el comportamiento de estos voladizos es bastante sencillo:
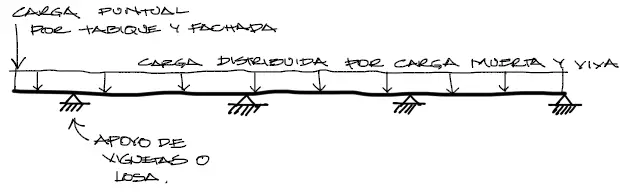
Voladizo de losa en 2 direcciones
A diferencia del voladizo anterior, una losa también puede volar apoyando sobre vigas que vuelan.
En este caso los elementos que vuelan son principalmente las vigas. A partir de este razonamiento, el voladizo puede ser más grande, aunque también más complejo de calcular.
En este tipo de estructura, la losa está apoyada en tres bordes, donde por lo menos uno de ellos es continuo. El cálculo tanto de deflexiones como de solicitaciones de este tipo de voladizo es más complejo, pues entran más variables en el cálculo.
Se podría pensar que sería adecuado armar la losa del voladizo en la dirección perpendicular a las vigas que vuelan, sin embargo eso no es del todo adecuado, ya que se debe procurar a toda costa buscar la redundancia (mayor candidad de apoyos) de la losa para que la carga se redistribuya mejor en todo su contorno y no solo en las vigas que vuelan.
Lastimosamente es difícil estimar a priori cual será la longitud de voladizo máxima alcanzable de este tipo de volado. Dependerá mucho de factores como
– Peralte de viga
– Peralte de losa
– Distancia entre vigas
– Continuidad de la losa respecto a paños adyacentes
– carga en la losa.
El modelo matemático que nos permitirá estimar tanto solicitaciones como deformaciones esquemáticamente es como sigue:
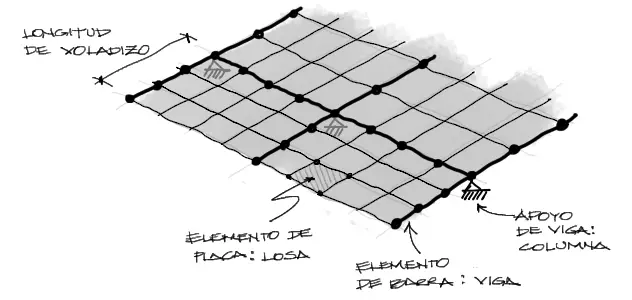Los apoyos en este caso pueden ser apoyos fijos o incluso elementos de barra verticales que emulen columnas. La losa mostrada deberá estar dividida en elementos de placa, lo suficientemente pequeños para que las solicitaciones sean precisas.
Voladizo de losas sin vigas
Este es en cierta manera solo un caso particular al anterior. Sin embargo esta losa en particular solo tiene dos apoyos en dos bordes.
Muchas veces la arquitectura no permite que se utilicen vigas en los bordes de la losa en voladizo y esta resulta ser menos rígida que en la losa del inciso anterior. Esto obviamente repercute en mayores deformaciones.
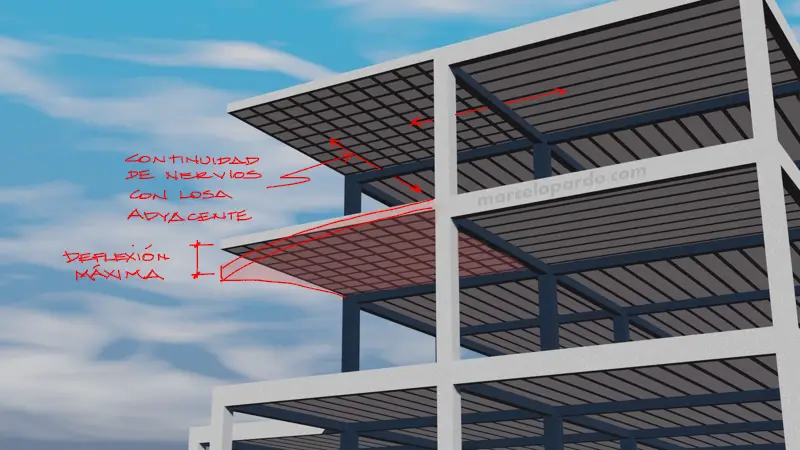Debido a las grandes deflexiones que puedan presentar debido a su esbeltez, este tipo de losas es recomendable usarlas solo en terrazas y zonas donde se vaya a estar seguro que la losa no recibirá carga significativa, y donde las deformaciones del voladizo no vayan a generar fisuras en elementos no estructurales frágiles como vidrio o mampostería.
grandes voladizos
Un tipo de voladizo que está muy de moda particularmente en estilos arquitectónicos minimalistas es el voladizo de grandes luces como el de la siguiente imagen:
Suelen consistir en voladizos francos de 4 o 5 metros, o incluso más. Este tipo de voladizos sin embargo requieren un cálculo estructural especial. Son algunos los aspectos que deben cuidarse al momento de diseñarlos.
Primeramente, nos daremos cuenta de que en las caras laterales de este tipo de voladizos, generalmente se tienen pocas aberturas o si se tienen aberturas, estas consisten en ventanales que ocultan la estructura lateral metálica que atraviesa de piso a techo del voladizo. Esto se debe a que estos muros laterales funcionan como grandes vigas que sostienen el voladizo.
Por otro lado, esta viga no puede terminar al arranque del voladizo, sino que debe penetrar hacia la estructura por lo menos una distancia igual a la distancia del voladizo. Mejor si atraviesa toda la estructura hasta su parte posterior opuesta al voladizo.
Además, se observa en la imagen, que las columnas al pie del voladizo son bastante robustas. Esto no es casual, ya que todo el peso del voladizo recae en estas columnas. Incluso el peso de la estructura del lado opuesto de la viga de gran altura recae sobre estas columnas, dejando prácticamente descargadas a las columnas posteriores.
Se puede notar en la siguiente imagen la integridad de las vigas de grán altura y como las viguetas de la losa se apoyan perpendiculares a la dirección de estas vigas, que recalgo, deberán en general tener pocas aberturas de puertas y ventanas.
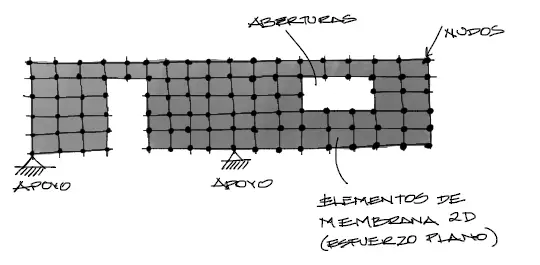
El modelo matemático que permite la simulación de este tipo de estructura está basado en elementos planos de membrana, con esfuerzos y solicitaciones paralelos a su plano, como en la siguiente imágen.
Voladizos de varios pisos
A medida que la estructura va tomando altura, los voladizos independientes para cada piso pueden reemplazarse por una estructura reticular que trabaje conjuntamente para resistir el voladizo de todos los niveles, como en la estructura mostrada a continuación.
Aunque pudiera parecer contraintuitivo, a medida que el voladizo crece en altura, gana rigidez. Si bien la cantidad de losas aporta carga al voladizo, la configuración reticulada de la estructura ayuda a transmitir la carga a la columna inferior de manera eficiente a partir de las diagonales.
Al igual que en la estructura de voladizo de la sección anterior, las columnas más cargadas son las del arranque del voladizo, con solicitaciones axiales que pueden ser hasta 10 veces más grandes que de las columnas aledañas.
Adicionalmente, se puede apreciar que las diagonales se construyen incluso en sectores que ya no pertenecen al voladizo. Esto se debe a que si no se las implementara de esta manera, las deformaciones en el sistema aporticado serían excesivas. Las diagonales que continuan hasta la parte trasera de la estructura opuesta al voladizo ayudan a absorber los grandes momentos flectores que se generarían en las columnas en ausencia de las primeras.
Salvo en sectores donde sea inminente la supresión de estas diagonales, éstas deberán proveerse en casi todo el sistema aporticado en la dirección paralela al voladizo.
Conclusiones
Dependiendo de la luz a volar, la solución estructural al problema de sostener el voladizo será distinta para cada caso. En general sin embargo, el voladizo siempre debe cumplir a las verifiacciones de deformación y resistencia. Si el voladizo no sostiene elementos frágiles no estructurales, la deflexión admisible a largo plazo podrá tomarse igual a L/480, pero si el voladizo contiene elementos susceptibles a dañarse con la deformación, será cauto que la deflexión real no sobrepase L/960. En ambos casos L es la luz del voladizo.
Vídeo
autor: Marcelo Pardo
Buen dia ingeniero, antes que nada muchas gracias por el articulo y muy clara la explicacion, ojala pudiera resolverme una duda sobre estos conceptos aplicados a zapatas en esquina, dada la similitud de estas zapatas con un voladizo en dos direcciones apoyada sobre vigas de equilibrio, usualmente calculo el cortante ultimo de estas zapatas considerando una longitud L completa de la zapata, sin embargo, al verificar este esfuerzo en algun software este cortante se comienza a manifestar desde la mitad de la longitud hasta el final de la zapata, es decir, una Longitud L/2, dado lo que comenta sobre la dificultad de calculo de esfuerzos en un voladizo en dos direcciones, es correcto asumir un cortante ultimo considerando una longitud L/2 para todos los tipos de zapatas(intermedias, colindantes, esquineras), quedo pendiente de sus comentarios, muchas gracias….
Angel buenas tardes!!
Francamente no estoy entendiendo tu pregunta muy bien, lastimosamente….
Una Disculpa Ingeniero, en resumen, para el calculo del cortante en particular, en el caso de voladizo de losas sin vigas, hay alguna manera o forma aproximada de calcular esta fuerza en estos elementos(similares a zapatas en esquina), tengo la duda si es valido el calculo de cortante en una direccion considerando un cortante por cada dimension(largo y ancho) de la losa, muchas gracias….
Angel, el cálculo de cortante se realiza de igual manera que en una zapata. cortante por punzonamiento al rededor de la columna. Esta zona es la más crítica, incluso en voladizos
Muchas gracias por su respuesta ingeniero, si de hecho mi duda surge ya que usualmente en zapatas tambien calculo la tension diagonal, el cual no supera al punzonamiento en zapatas intermedias, sin embargo, en zapatas en esquina haciendo la analogia en voladizos el calculo seria asi: Vu=Wu*b*L, siendo L la longitud total de la zapata, el cual es el doble a su contraparte de zapata intermedia, entonces para reafirmar, esta analogia seria herrada y el punzonamiento es el que rige en estos casos?, muchas gracias
Buen dia Ingeniero, he hecho algunas investigaciones y me respondo a mi mismo, cuando se omiten vigas de equilibrio en una zapata en esquina es como usted menciona, los maximos esfuerzos son generados por punzonamiento, ademas de que los esfuerzos por cortante diagonal y la flexion toman en cuenta la longitud total de la zapata, sin embargo, al agregar vigas de equilibrio guardando la similitud con volados apoyados en dos direcciones, estos esfuerzos analizados por software son inferiores a su contraparte de zapata intermedia, por lo tanto de manera empirica se podrian calcular igual que esta ultima para fines practicos, aun asi seria prudente hacer un analisis mas detallado por software para verificar resultados, gracias por sus conocimientos, saludos….
Muy buena la Explicacion….!!!
Muchas gracias Marin!
EXCELENTE EXPLICACION, UNA GRAN FELICITACION.
Gracias Federico!!!
Claro, conciso y concreto.
Muy bien