Técnicas de Modelado de Muros de Mampostería en software estructural

Contexto

Cuando necesitamos diseñar una estructura con elementos de mampostería confinada, la selección del tipo de modelo matemático a usar no es trivial.

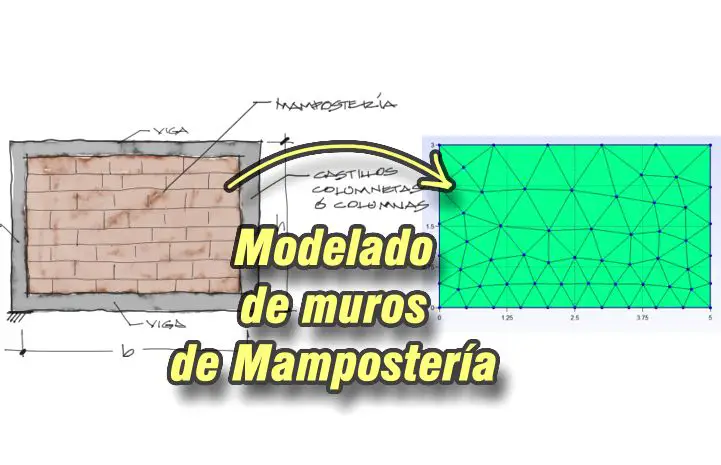
La interacción entre dos materiales con rigideces tan distintas (ladrillo y hormigón) hace que debamos tomar ciertas consideraciones sobre el modelo matemático que debamos usar para modelar y diseñar la estructura.

De hecho, un panel de mampostería es mucho más rígido que un marco hueco aporticado. Tanto es así que si apliaramos una carga lateral a una combinación de un paño de mampostería confinado por vigas y columnas de hormigón armado, la mamposteria al deformarse mucho menos que el marco de hormigón armado, forma una biela de compresión diagonal en la transversal más corta deformada del marco, como se ve en la imagen:

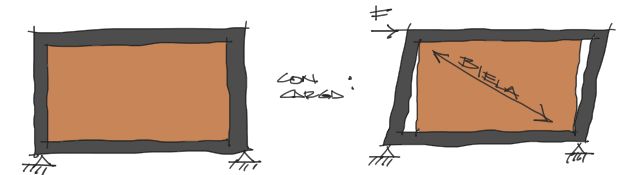
A partir de este fenómeno, se han desarrollado diferentes teorías de modelado de este fenómeno matemáticamente para predecir el comportamiento de una estructura con estos elementos.

Elementos diagonales equivalentes

Una manera de modelar un muro de mampostería de manera sencilla en programas de cálculo estructural básicos sin el uso de elementos de placa (shell) es con el uso de elementos de barra diagonales de rigidez equivalente al de la mampostería.

Se busca reemplazar la mampostería de un marco cerrado, por un elemento de barra diagonal que tenga una rigidez similar:

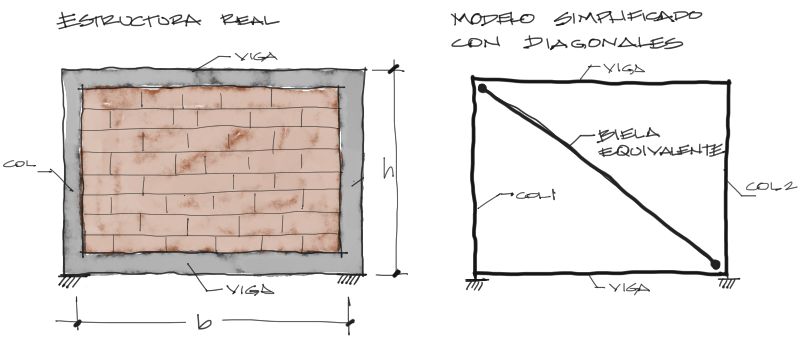
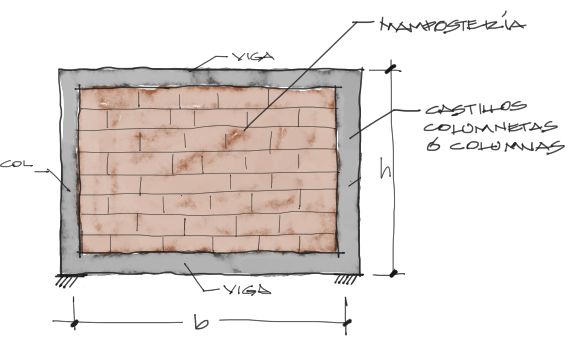
En el libro de Bazan y Meli de diseño de edificios, se explica el método donde, para dimensiones de mampostería como las de la siguiente figura:

,se aplican las siguientes fórmulas para convertir el elemento de mampostería en una barra de sección transversal de ancho “w” y espesor “t”:

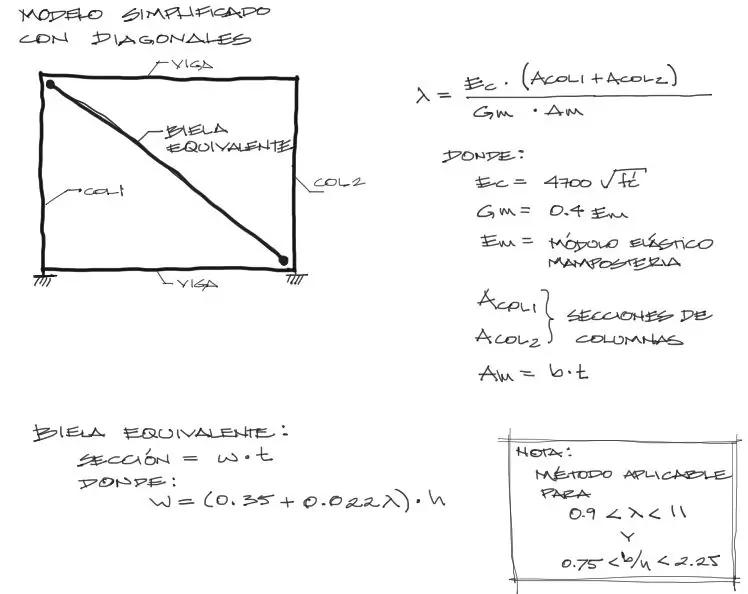
Se debe encontrar un factor λ que siempre que esté entre 0.9 y 11, el método es aplicable. Así también b/h debe estar entre 0.75 y 2.25. Ambos rangos abargan la mayoría de los casos prácticos de análisis.

A partir de λ se puede calcular el ancho “w” de la biela diagonal equivalente. Con este dato se tiene la sección transversal de la diagonal y ésta se modela como un elemento de pórtico inclinado como en la figura arriba, reduciendo grandemente la cantidad de nudos de un modelo de elementos finitos y haciendo la estructura mucho más fácil de revisar.

De las fórmulas arriba mostradas, los únicos datos que no conocemos son Em y Gm que corresponden al módulo elástico y módulo de cortante de la mampostería. Por lo general se toma Em = 600*fm donde fm es la resistencia de diseño de la mampostería. Su resistencia variará mucho en función al proceso de fabricación de los ladrillos. El rango de resistencias común irá entre 1.5 a 4 MPa, sin embargo puede llegar a resistencias tan altas como 15 MPa en algunos casos.

Columna ancha Equivalente

Otra alternativa de modelado de los peneles de mampostería confinada consiste en transformar todo el muro en una columna equivalente con una rigidez combinada de flexión más cortante.

Este modelo está conformado por la inercia por flexión de las columnas de los extremos más la rigidez por cortante aportada por el muro. Se utiliza el mismo factor λ del anterior método para el cálculo de la sección equivalente Ω.

Una vez calculados Ω e Ic, el cálculo del desplazamiento δ producto de una carga lateral aplicada en la cima es la mostrada.

Elementos Finitos

Este es el método más popular hoy para el modelado matemático de placas de mampostería en un sistema estructural. Sin embargo se debe tomar con pinzas el uso de estos elementos pues muchas veces se pasan por alto las buenas prácticas de la forma geométrica de los elementos

Otro factor a tomar en cuenta al momento de usar elementos finitos es el número de elementos a utilizar en el modelado del panel de mampostería, o si se deben utilizar elementos de membrana que solo reciben cargas paralelas al plano, o elementos que absorben fuerzas incluso perpendiculares al plano de análisis.

En el caso de modelos en 2 dimensiones la elección es obvia. se modelan con elementos de membrana. Para el caso del presente análisis basta con utilizar un elemento rectangular de 4 nudos (8 grados de libertad) cuya matriz de rigidez es la siguiente:

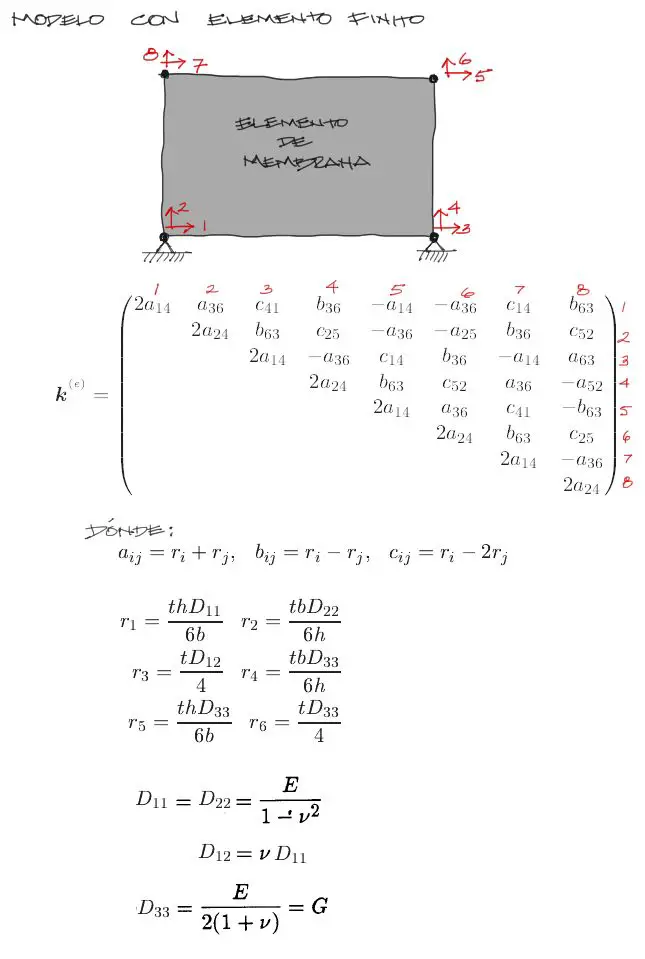
El uso de esta matriz de rigidez en el cálculo de deformaciones de la estructura consiste en un procedimiento de álgebra lineal que se explicará mejor en un ejemplo en la siguiente publicación.

Es recomendable cuando se modelan muros de mampostería con elementos finitos, no utilizar demasiados elementos como en la imagen de la portada. Esto puede dificultar la fluidez de cálculo del modelo matemático, así como el cálculo de los modos naturales de vibrar de la estructura.

Modelado de estructura con diagonal equivalente

Hice un vídeo donde explico un poco de la teoría expuesta en esta publicación y adicionalmente aplico la teoría de diagonal equivalente a un ejemplo práctico.