Antecedentes
Los perfiles metálicos de sección W son laminados en caliente. Es por esta propiedad que debemos aplicar directrices y normativas aplicables a este tipo de fabricación. La que usaremos en este caso será la norma AISC 360-16.
Por otro lado, nos interesa realizar las comprobaciones en estado límite último (LRFD) por ser un método más moderno de cálculo de resistencias.
Factor de reducción
Bajo la normativa mencionada y en estádos límites (LRFD), el factor de reducción de resistencias aplicado a la resistencia nominal será:
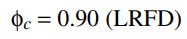
Por tanto, la resistencia de diseño ɸFn será igual a 0.9*Fn
Comprobaciones
Se deben distinguir dos tipos de secciones para elementos a compresión. Las secciones NO ESBELTAS y las secciones ESBELTAS. La diferencia entre estos dos tipos de secciones está controlado por la relación Ancho/Espesor de cada una de sus caras. Si esta relación es muy alta (comparada con valores límite explicados a continuación), la sección es esbelta, y de otra manera es corta.
Las secciones esbeltas se diferencian de las secciones cortas en la cantidad de comprobaciones a las que deben ser sometidas. Al tener las caras muy delgadas, las secciones esbelta son susceptibles a pandeo local de una de sus caras, además de la posible falla por pandeo por flexión y pandeo por torsión que podrían sufrir.
En resumen, las comprobaciones a las que se debe someter un perfil W a compresión son:
Para Secciones NO ESBELTAS:
- Pandeo por Flexión
- Pandeo por Torsión
Para secciones ESBELTAS:
- Pandeo por Flexión
- Pandeo por torsión
- Pandeo Local
Para perfiles W la falla de pandeo por torsión no suele controlar el diseño (o sea, no suele ser motivo de falla del perfil). Sin embargo se lo incluye para propósitos de verificación en caso de utilizar secciones de pared muy delgada.
Comprobación de esbeltez
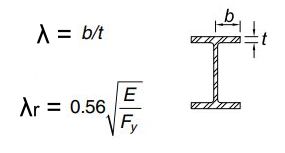
Para determinar si la sección es esbelta o no, se debe calcular la relación λ = b/t para cada una de las caras del perfil.
Para el alma de la sección W, b es la distancia entre las dos alas. Para el ala de la sección W, b es la distancia libre desde el centro del ala hasta el extremo.
Para el ala:
Para el alma:
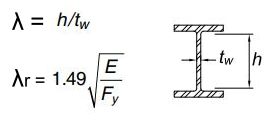
En ambos casos, si la relación λ es mayor a λr para el alma,para el ala, o para ambas, la sección se considera esbelta. De otra forma es NO ESBELTA.
Longitud efectiva
La longitud con las que se realizan los cálculos del pandeo de columnas no es la longitud real de la columna, sino la longitud efectiva, afectada por el factor K de longitud efectiva:
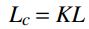
Se debe tener en cuenta por tanto el grado de arriostramiento de la estructura, asi como el tipo de conexión de los extremos para conocer este factor K.
En general, la verificación debe realizarse para los dos ejes, X y Y. Si las longitudes efectivas en ambas direcciones no son iguales, deberá discriminarse K en Kx y Ky.
Luego, independientemente de si Kx y Ky son iguales o distintos, el análisis de pandeo por flexión debe hacerse en las dos direcciones. Para perfiles W, la resistencia Pn suele estar controlada por el pandeo en el eje débil del perfil (dirección Y).
SECCIONES NO ESBELTAS
Pendeo por flexión de sección no esbelta
La resistencia nominal Pn se calcula con:
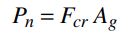
donde Fcr se calcula por:
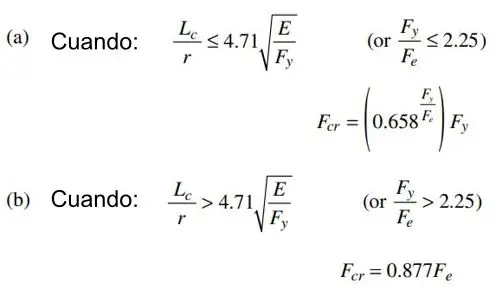
Además para estas fórmulas, Fe se calcula con:
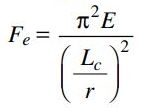
Pandeo por torsión de sección no esbleta
La resistencia nominal Pn se calcula con:
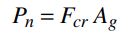
donde Fcr se calcula por:
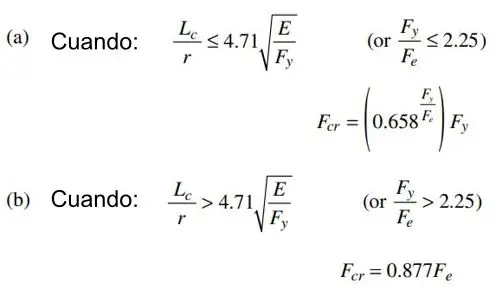
En esta última fórmula Lc/r corresponde a la esbeltez más grande entre Lcx/rx y Lcy/ry.
Esta vez, Fe es calculado con:
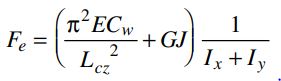
De esta última fórmula:
- Cw: Constante de alabeo
- G: Módulo de cortante (77200 MPa)
- J: Constante Torsional
- Lcz = Kz*Lz: Longitud efectiva a lo largo del eje longitudinal
La variable Lcz se calcula en función a la capacidad que tiene la columna de rotar respecto de su eje, por tanto el factor Kz corresponde a la longitud efectiva por torsión.
SECCIONES ESBELTAS
Pandeo por flexión de sección esbelta
La resistencia nominal Pn se calcula con:
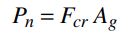
donde Fcr se calcula por:
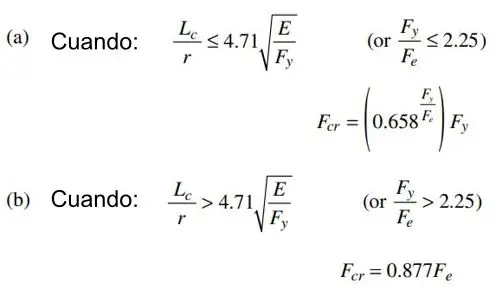
Además para estas fórmulas, Fe se calcula con:
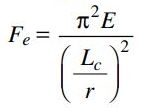
Pandeo por torsión de sección esbelta
La resistencia nominal Pn se calcula con:
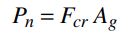
donde Fcr se calcula por:
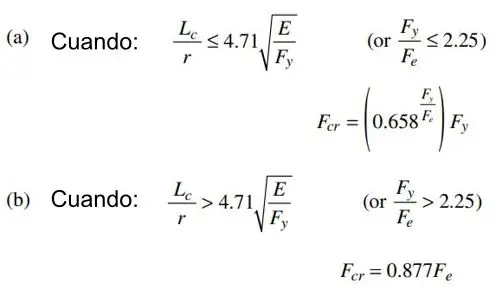
En esta última fórmula Lc/r corresponde a la esbeltez más grande entre Lcx/rx y Lcy/ry.
Fe es calculado con:
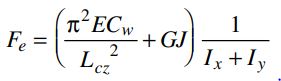
De esta última fórmula:
- Cw: Constante de alabeo
- G: Módulo de cortante (77200 MPa)
- J: Constante Torsional
- Lcz = Kz*Lz: Longitud efectiva a lo largo del eje longitudinal
La variable Lcz se calcula en función a la capacidad que tiene la columna de rotar respecto de su eje, por tanto el factor Kz corresponde a la longitud efectiva por torsión.
Resistencia crítica Fcr
Tanto para secciones esbeltas como no esbeltas se han obtenido varios Fcr para verificación de pandeo a flexión en X, pandeo a flexión en Y, y pandeo por torsión Z. La fuerza resistente Fcr será la menor de las 3 calculadas.
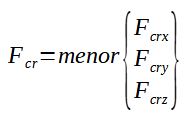
Sección efectiva
Si estamos en esta sección del artículo es porque λ ha superado a λr en el alma, ala, o ambos. Toca entonces reajustar el área bruta “Ag” y convertirla en área efectiva “Ae” de la sección.
Cuando, para ala o alma λ<λr:
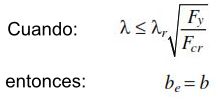
Cuando, para ala o alma λ>λr:
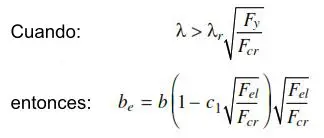
Y para esta última fórmula:
- be: Ancho efectivo del alma o ala
- c1 = 0.18 para el alma
- c1 = 0.22 para las alas
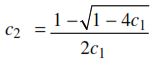
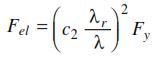
- Fcr: Esfuerzo crítico calculado en pandeo por flexión o torsión (el menor de ambos)
A partir del ancho efectivo be para cada tramo de ala o para el alma, se calcula la sección efectiva “Ae” deduciendo de “Ag”, la expresión (b-be)*t para todos los tramos donde be sea menor que b. finalmente:
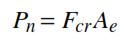
Consideraciones adicionales
En el vídeo explico algunas puntualizaciones necesarias respecto al pandeo en ambas direcciones en perfiles W
autor: Marcelo Pardo
←←← VOLVER A TABLA DE CONTENIDO DE ESTRUCTURAS METÁLICAS ←←←


