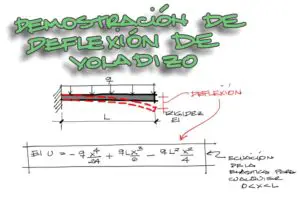
Enunciado

El ejercicio se encuentra propuesto en el libro de Singer, ejercicio 235.

Un bloque completamente rígido de masa M se apoya en tres varillas situadas en un mismo plano, como indica la figura abajo. Las varillas de cobre tienen una sección de 900mm2 y un E = 120GPa. El esfuerzo admisible del cobre es de 70MPa. La varilla de acero tiene una sección de 1200mm2, E=200GPa y el esfuerzo admisible de 140MPa. Calcular la máxima masa M que pueden soportar las varillas.

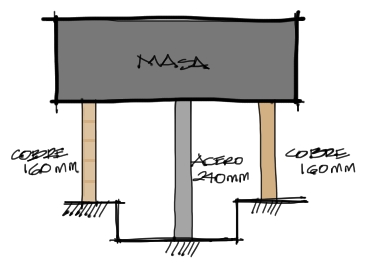
Equilibrio del sistema

El ejercicio conlleva conceptos de
– Esfuerzo axial
-Deformación unitaria.

El primer paso consiste siempre en el equilibrio del sistema. Aprovechamos la simetría del sistema para saber que el bloque M desciende pero no rota. A partir de este razonamiento:

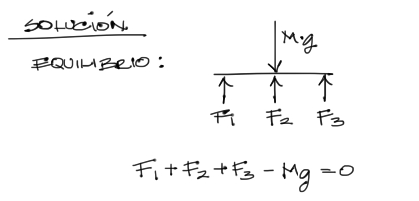
Esfuerzo deformación

Por otro lado debemos razonar sobre la relación fuerza – deformación que existe en cada barra. Par eso citamos la fórmula de esfuerzo = E·Deformacion_unitaria, luego descomponemos el esfuerzo en fuerza y la deformación unitaria en deformación sobre longitud. Comenzamos con la fuerza F1 y F3 que son iguales:

Para la fuerza F2 se repite el procedimiento:

Razonamiento sobre las deformaciones

Si bien las deformaciones unitarias ξ1 ξ2 ξ3 no son iguales entre sí, lo que si es igual es el desplazamiento absoluto vertical del bloque por si naturaleza rígida. Por tanto:

Luego reemplazamos todos los datos en la ecuación de equilibrio F1+F2+F3-Mg = 0

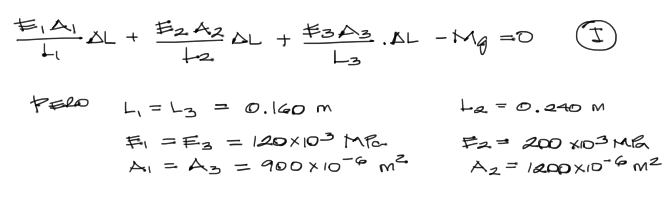
Se reemplazan todos los datos y se tiene:

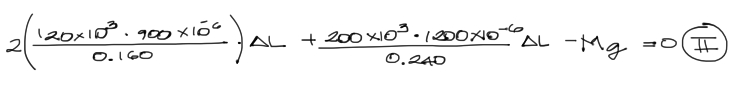
Esfuerzo y deformación admisible

Los esfuerzos admisibles de ambos materiales, cobre y acero, son los siguientes:

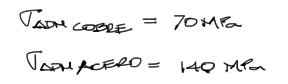
Esto quiere decir que los esfuezos en las varillas no deben exceder estos esfuerzos. Sin embargo la ecuación de equilibrio II del anterior subtítulo está en función de la deformación absoluta ΔL de las tres barras. Debemos entonces transformar este esfuerzo admisible en deformación admisible para las tres varillas:

La relación entre deformación ΔL y el esfuerzo es directa. Encontramos entonces cual es el ΔL máximo que pueden deformarse las tres vaillas:

De las tres varillas, la que controla el diseño es la deformación de la varilla de cobre. El razonamiento es como sigue: Si la vailla de cobre se deforma más que 9.333e-5 m fallará, por otro lado si la barra de acero se deforma más que 16.8e-5m también fallará. como todas las barras se deforman al mismo tiempo, para el momento en que la vailla de cobre comience a fallar a 9.333e-5m a la varilla de acero aun le quedará deformación disponible antes de la falla. Es por eso que las varillas de cobre controlan el diseño.

Resultado final

Realizamos el reemplazo de ΔL = 9.333e-5 dentro de la ecuación de equilibrio II encontrada anteriormente y despejamos primero el peso W = M·g. Hecho esto la masa es despejada con facilidad.

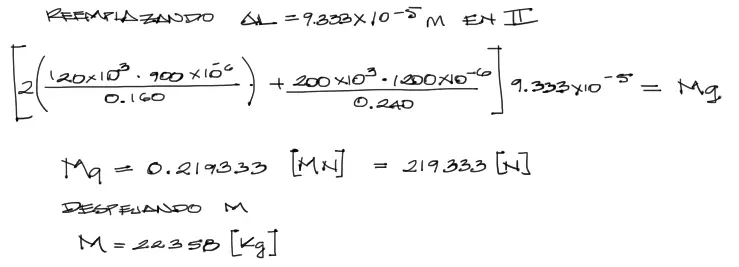
Debe tomarse en cuenta que las unidades con las que se trabajó para el módulo elástico es de MPa, además las unidades de sección transversal y longitud también fueron transformadas a metros. El resultado entonces estará en [MN] (megaNewtons). Luego se hace la transformación a Newtons y finalmente despejamos la masa en Kilogramos.

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE RESISTENCIA DE MATERIALES ←←←