Teoría
Existen muchas maneras de resolver sistemas de ecuaciones lineales. Entre uno de los más conocidos en métodos numéricos está el método de Eliminación de Gauss. Existen métodos como el de la inversa de la matriz o la Descomposición LU. También existen métodos iterativos para matrices de gran tamaño como el de Gradientes conjugados.
En este artículo se verán maneras de resolver sistemas de ecuaciones por varios de estos métodos.
Ejemplo: La matriz a resolver
Se plantea resolver el siguiente sistema de ecuaciones:
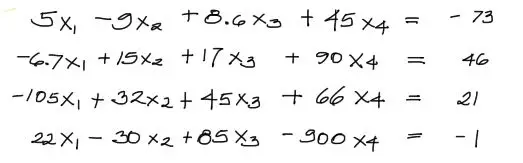
El sistema se puede reducir a la siguiente expresión
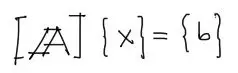
donde,
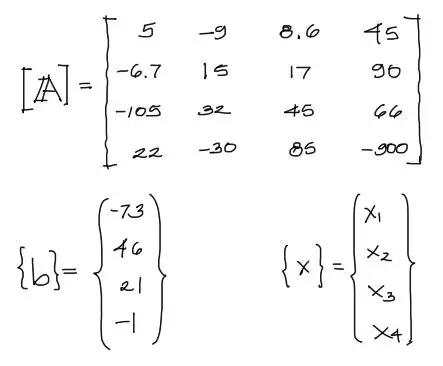
Este sistema puede resolverse mediante los siguientes comandos de OCTAVE
Solución
Como se vio en el artículo almacenar matrices y tensores, definimos y almacenamos una matriz cuadrada dentro de una variable que llamaremos A

Posteriormente hacemos lo mismo con el vector {b}
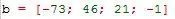
La solución de este sistema puede resolverse por cualquiera de los siguientes comandos:
Inversa de A
Almacenamos el resultado dentro de sol_1, invirtiendo [A] y multiplicandola por {b}:
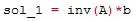
El resultado en la consola es:

A\b
Similar al anterior comando, se puede encontrar la solución al sistema lineal mediante:
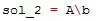
obteniendose exactamente el mismo resultado pero almacenado en sol_2
rref
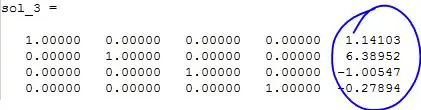
Podemos recurrir a la reducción escalonada de la matriz cuadrada meduante rref. Sin embargo primeramente se debe concatenar tanto la matriz A como el vector b lado a lado mediante [A b], e introducir esta matriz concatenada dentro del comando rref. Se guardará el resultado dentro de una variable sol_3:
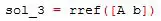
El resultado en este caso será algo distinto a los dos anteriores, pues antes de mostrar los valores x1 a x4, muestra la matriz escalonada reducida que es igual a la matriz identidad, que en este caso es 4×4:
linsolve
Existen varias opciones dentro del comando linsolve para resolver sistemas de ecuaciones. Entre ellos, el comando puede resolver matrices triangulares superiores o triangulares inferiores entre otras. Sin embargo OCTAVE recomienda que sea el propio programa el que escoja cual de los métodos aplicar según los argumentos introducidos. En este caso se usan los valores por defecto y se almacenan los resultados en sol_4:
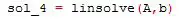
El resultado es idéntico al de los dos primeros métodos.
cgs (iterativo)
Este comando utiliza el algoritmo de gradientes conjugados para resolver iterativamente sistemas lineales de ecuaciones. Se guardan los resultados en una variable sol_5:
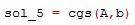
Otros algoritmos
Existen otros algoritmos más especializados de resolución de sistemas lineales, pero con los mostrados ya tienes suficientes armas para resolver sistemas lineales de ecuaciones convencionales sin problemas. Todos los métodos mencionados deberían darte el mismo resultado
autor: Marcelo Pardo