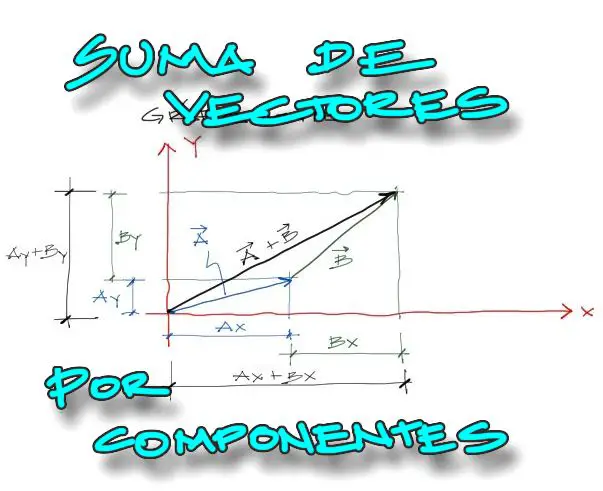
Componentes de un vector
Entre los métodos de suma de vectores, el uso de componentes de un vector para la suma vectorial es el más popular y conocido.
Cualquier vector puede representarse completamente a partir de sus componentes. Estos vectores pueden estar representados en un plano o en el espacio, por lo que requerirán 2 o 3 componentes respectivamente.

La representación de vectores por componentes mostrada arriba corresponde a una notación tipo vector fila. Otros tipos de notación que representan al mismo vector son las siguientes:

En todos los casos, la primera componente reprenta la magnitud del vector en el eje X, la segunda en el eje Y (y la tercera en el eje Z)
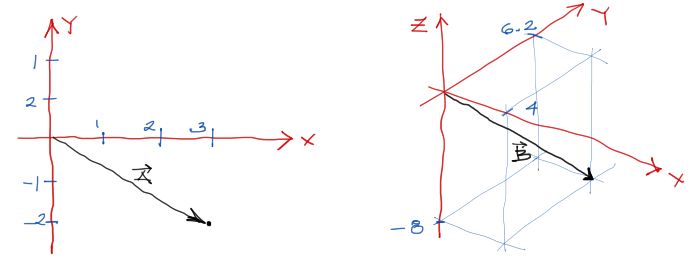
Suma de componentes
Cuando se suman dos (o más) vectores por componentes, el resultado serán las componentes de otro vector final. La suma por componentes es muy sencilla, y consiste en sumar las compoenentes en X de dos (o más) vectores, luego las componentes en Y, y si se tratara de un cálculo en el espacio, las componentes en Z:

Si se quiere utilizar la notación en base a vectores unitarios, la notación es la siguiente:
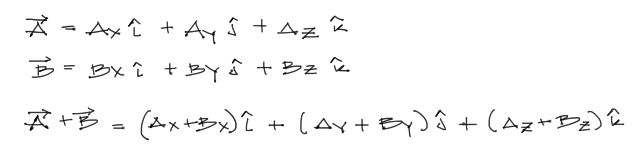
Sin embargo, en lo personal este tipo de notación me resulta más confusa que la primera.
Gráficamente sucede lo siguiente en 2 dimensiones:
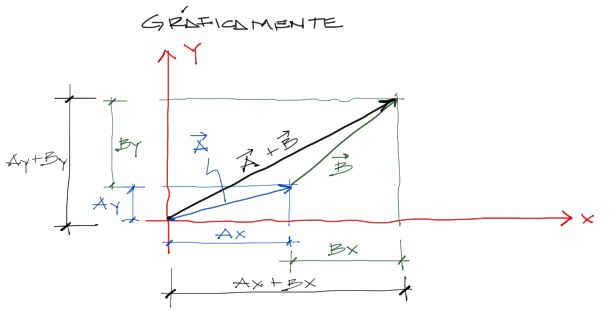
En 3 dimensiones sucede algo similar.
La mayor dificultad suele radicar en encontrar las componentes de cada vector antes de sumarlos, sin embargo cuando ya se encontraron estas componentes, la suma es inmediata.
Magnitud y dirección del vector resultante
Una vez calculado el vector resultante, se puede obtener su magnitud tanto en 2 como en 3 dimensiones a partir de:
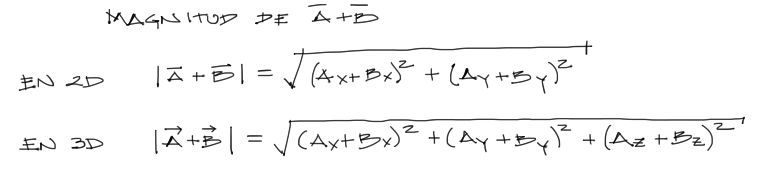
Si se desea conocer la dirección del vector resultante respecto al eje X positivo en 2 dimensiones, puede calcularse con el arcoseno de la componente X entre la magnitud del vector:
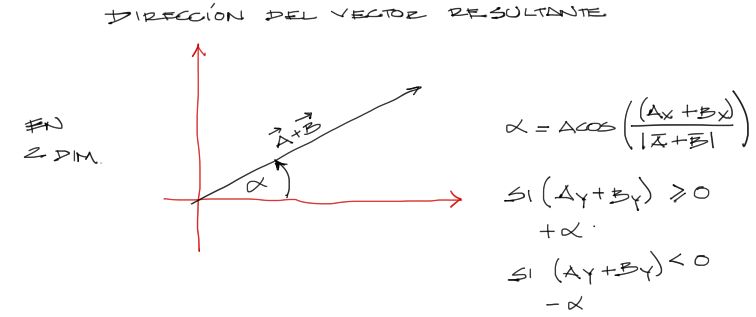
Debemos notar que tanto para vectores resultantes que pertenecen al cuadrante I, II, como a III y IV, el ángulo obtenido será siempre positivo a partir de arcoseno. Para determinar finalmente si el ángulo de dirección pertenece al cuadrante I o II (α positivo), o si pertener al cuadrante III o IV (α negativo), se debe aplicar la condicionante de la figura.
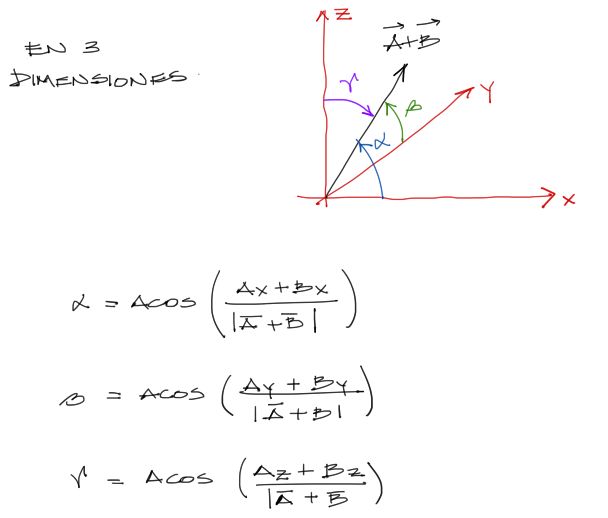
Para calcular la dirección de un vector en 3 dimensiones, es suficiente con aplicar cosenos directores y así obtener el ángulo al vector desde cada uno de los ejes coordenados:
autor: Marcelo Pardo
