Introducción

Generalmente no se entiende la aplicación directa del tema de transformación de esfuerzo pues los docentes clásicamente lo explican entrando directamente a las fórmulas y a su deducción.

Sin embargo el concepto de transformación de esfuerzo, más allá de las fórmulas tiene un trasfondo bastante útil.

Por ejemplo cuando calculamos las solicitaciones o los esfuerzos en un elemento como una viga o una columna, solemos hacerlo en caras perpendiculares al eje del elemento (casi siempre en cortes verticales u horizontales). Sin embargo muchas veces vamos a necesitar conocer los esfuerzos en una dirección distinta a la clásica mencionada.

Caso 1

Veamos por ejemplo el siguiente caso. Se trata de una ménsula que fue construida con la veta de la madera en dirección inclinada. Posteriormente se pueden obtener los esfuerzos de corte y momento flector en cortes verticales imaginarios realizados como en la imagen de la derecha.

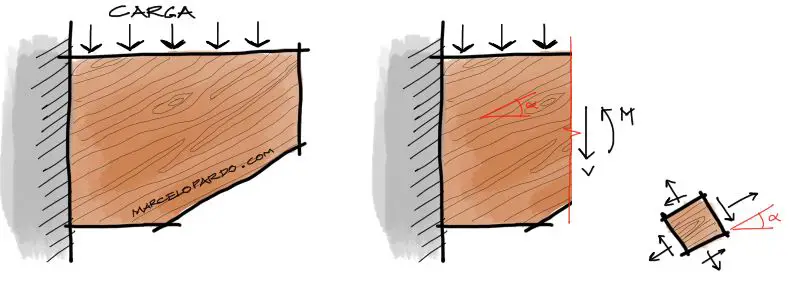
Sucede que por otro lado, suelen conocerse las resistencias de la madera en direcciones paralelas y perpendiculares a las fibras de la madera(que suelen ser diferentes según la dirección), por lo que los esfuerzos encontrados en la cara vertical no nos sirven mucho para saber si la madera resiste dichos esfuerzos. Es entonces cuando debemos rotar los esfuerzos solicitantes a la dirección mostrada para poder compararlos con la resistencias del material.

Caso 2

Un ejemplo clásico consiste en el análisis de taludes. Para su análisis se debe conocer el factor de seguridad del talud dividiendo los esfuerzos solicitantes entre los esfuerzos resistentes. El inconveniente resulta al hacer un análisis mediante elementos finitos del talud, donde los esfuerzos suelen alinearse en función al sistema coordenado mostrado en la figura.

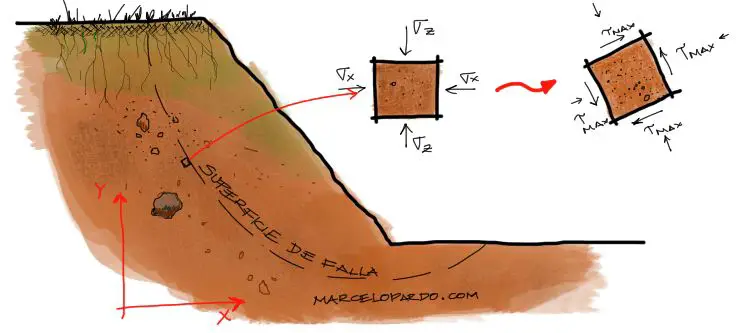
Además sabemos que cuando hablamos de suelo, la falla suele producirse por esfuerzos cortantes en el suelo. Así que debemos conocer los esfuerzos cortantes máximos a lo largo de todo el talud y estos esfuerzos casi nunca estarán en dirección vertical u horizontal, alineadas con los ejes XY. Aquí es donde debemos aplicar conocimientos de rotación de esfuerzos para conocer los esfuerzos máximos cortantes en todos los puntos.

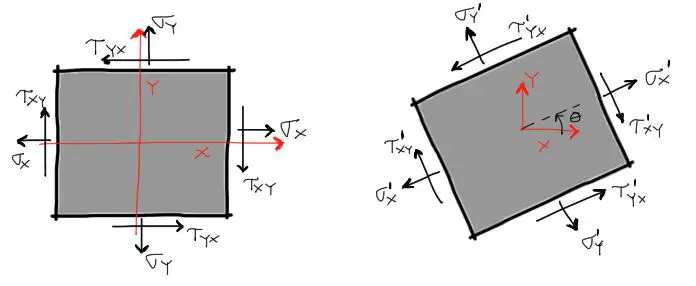
Convención de signos

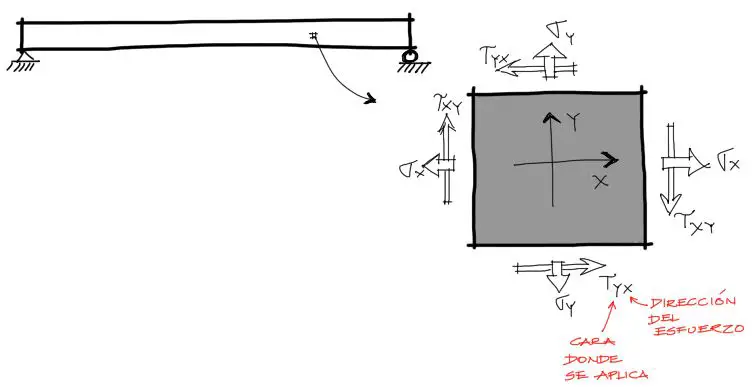
Diferentes libros y autores de resistencia de materiales tienen diferentes maneras de utilizar la convención de signos especialmente cuando se trata de cortantes. Para los esfuerzos axiales casi universalmente se convino que el esfuerzo a tracción es positivo y a compresión es negativo.

Respecto al esfuerzo cortante, se seguirá en este artículo la convención de signos mostrada en la imagen, donde el cortante positivo se dirige en las direcciones mostradas:

Por otro lado cuando deseamos transformar los esfuerzos rotándolos un ángulo θ, debemos elegir qué dirección adoptamos como positiva. Al igual que con el cortante, para otros autores la forma de asumir la dirección positiva es en sentido horario, sin embargo en este artículo se prefiere medir el ángulo en sentido Antihorario como positivo.

Fórmulas de transformación de esfuerzo

Sin entrar en demostraciones, las fórmulas de rotación de esfuerzos para transformar los esfuerzos originales alineados con los ejes XY hasta llegar a los esfuerzos rotados un ángulo θ son:

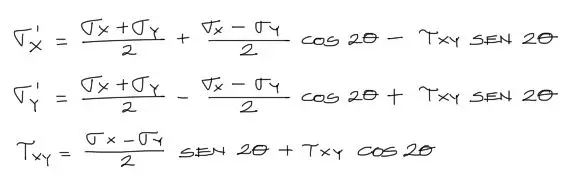
Esfuerzos Principales

Si lo que se desea es conocer el ángulo que logra que los esfuerzos axiales se hagan máximos o mínimos y el esfuerzo cortante se haga cero, se puede proceder a derivar las fórmulas anteriores respecto al ángulo e igualar la derivada a cero. así, despejando el ángulo θ se logran las siguientes expresiones:

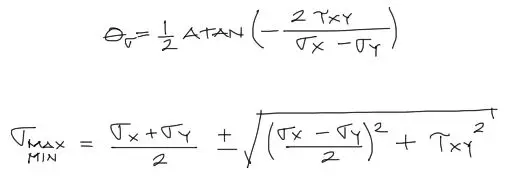
A la vez, si lo que se desea, como en el caso del talud, es encontrar los esfuerzos cortantes máximos, se pueden aplicar las siguientes fórmulas.

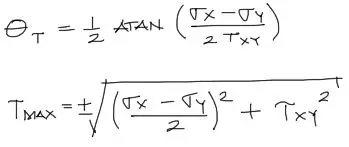
Nota que en estas fórmulas, a pesar de que los cortantes se hacen máximos, esto no quiere decir que los esfuerzos normales se anulen. Una vez encontrado el ángulo θT, se debe reemplazar este θT en las fórmulas de σx’ y σy’ para encontrar estos esfuerzos.

Círculo de Mohr

Si lo que quieres es conocer de forma gráfica las fórmulas expresadas en esta publicación, el siguiente esquema del círculo de Mohr de dará la idea completa.

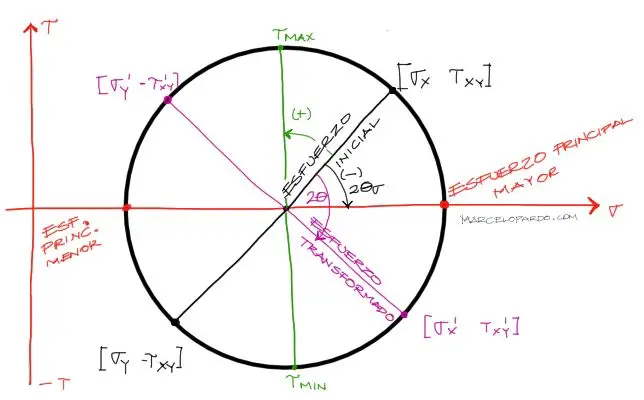
Los esfuerzos en Negro representan los esfuerzos iniciales. Los esfuerzos [σx,Ƭxy] se acompañan con los esfuerzos [σy,-Ƭxy] para dibujar la línea negra.

El ángulo de rotación se mide en sentido antihorario positivo. Si en las fórmulas de transformación de esfuerzo, para llegar de σx,σy,Ƭxy hasta σx’,σy’,Ƭxy’ se debe rotar un ángulo θ, en el círculo de Mohr, este círculo deberá ser del doble, 2θ. La línea magenta representa el esfuerzo transformado.

Los esfuerzos axiales principales son representados con un línea roja marcada justo sobre el eje horizontal.

Los esfuerzos cortantes principales se muestran con una línea verde. Nota que cuando los esfuerzos axiales principales se hacen máximos, el cortante se hace cero. Sin embargo cuando el cortante toma valores máximos, los esfuerzos axiales tienen valores correspondientes al centro del círculo de Mohr.

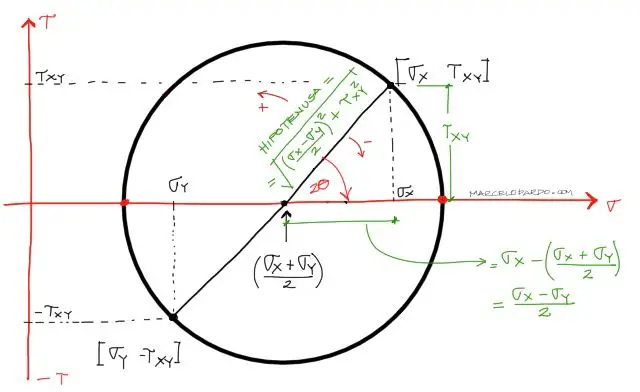
Geométricamente se puede descomponer el círculo de Mohr de la siguiente manera:

Video explicativo del círculo de Mohr

Hice hace varios años ya un vídeo donde explico el uso del círculo de Mohr así como su uso en un ejemplo aplicativo sencillo. Te invito a verlo a continuación:

autor: Marcelo Pardo

← ← ← VOLVER A TABLA DE CONTENIDO DE RESISTENCIA DE MATERIALES← ← ←