Antecedentes

Hasta este punto hemos conseguido calcular la matriz de rigidez global de la estructura y el vector de cargas puntuales. Los enlaces de dichos procedimientos están en:
– Matriz de rigidez de pórtico en 2 dimensiones.
– Vector de cargas puntuales de pórtico en 2 dimensiones.

Es recomendable que leas los dos artículos anteriores antes de avanzar con este.

Ecuación de equilibrio estático

Matricialmente la ecuación de equilibrio estático es la siguiente:

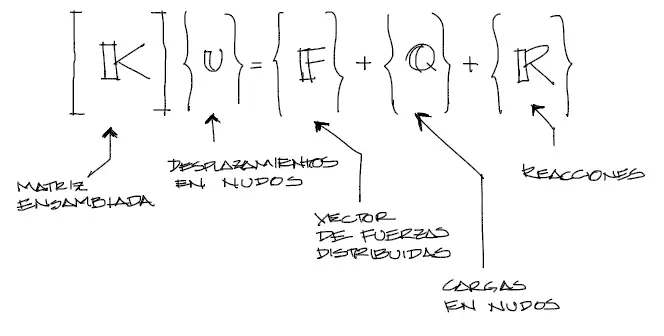
De esta ecuación ya se dedujeron y explicaron la ecuación de rigidez [K] y el vector de cargas puntuales [Q]. Ahora procederemos con el vector de cargas distribuidas [F]

Tipos de cargas distribuidas más comunes

Ante el problema del pórtico de la figura, los tipos de cargas distribuidas más comunes se dividen en 2 grandes grupos:
– Cargas perpendiculares al eje longitudinal de la barra
– Cargas paralelas al eje longitudinal.

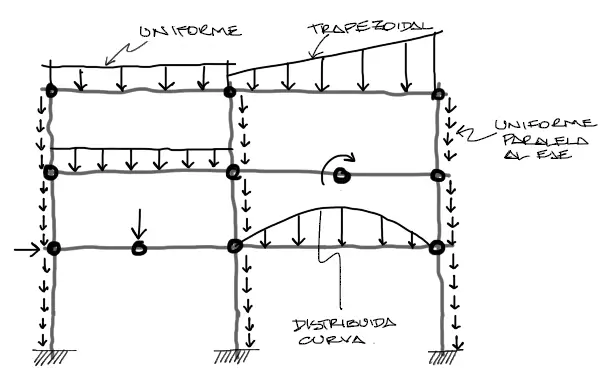
Las cargas paralelas al eje de la barra consisten normalmente en cargas por peso propio de columnas, donde a sección constante, la carga distribuida es también constante por unidad de longitud del elemento.

Por otro lado, entre las cargas perpendiculares al eje longitudinal, las cargas pueden clasificarse en uniformemente distribuidas, trapezoidales, triangulares, o incluso cargas curvas. Sin embargo como se verá a continuación, todas pueden generalizarse como casos especiales de una carga tipo trapezoidal.

Las cargas distribuidas uniformemente distribuidas consisten en una carga trapezoidal con los dos extremos iguales. Una carga triangular consiste en un trapecio con un extremo igual a cero. En ese sentido, podríamos clasificar las cargas distribuidas más bien en trapezoidales crecientes, uniformes y trapezoidales decrecientes, como sigue:

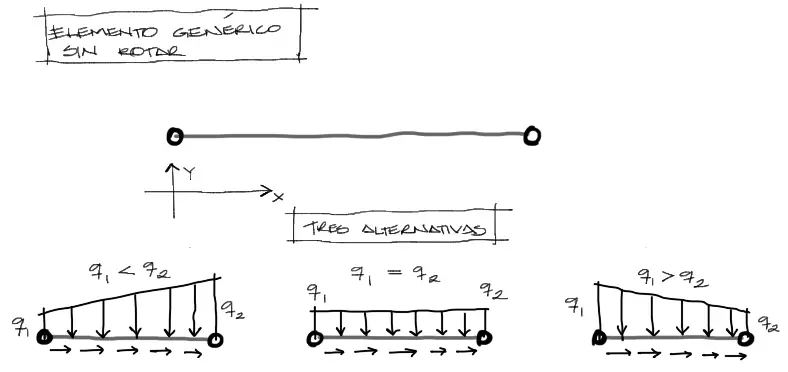
Las cargas mostradas en la figura deberán convertirse en cargas equivalentes en los nudos. Para lograr esto se utilizan las tablas de momento de empotramiento perfecto para las cargas perpendiculares a la barra. Para las cargas paralelas a la barra distribuimos la carga distribuida equitativamente entre ambos nudos, como se verá a continuación.

Caso de elemento con carga longitudinal y q1<q2

En esta situación asumimos primeramente que la carga longitudinal es uniforme, de tal manera se distribuye la carga «f» entre los dos nudos equitativamente. Como la resultante de la fuerza longitudinal es f*L, la carga que llega a cada nudo será f*L/2.

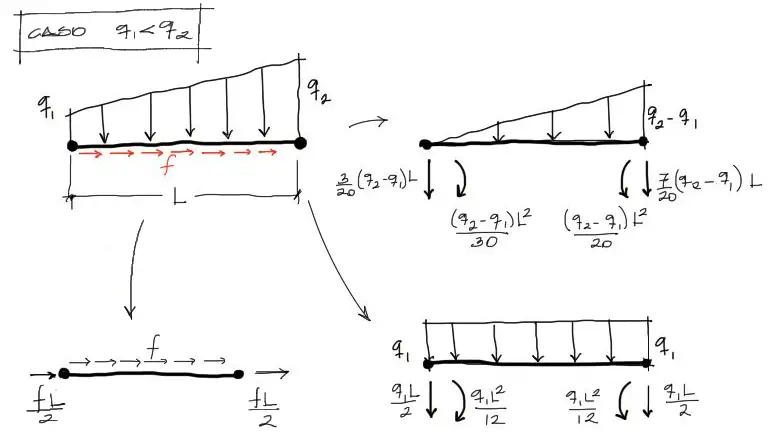
Por otro lado la carga trapezoidal se puede separa en una carga triangular y una rectangular y sumarlas luego por el principio de superposición.

Las cargas equivalentes en los nudos a partir de estas cargas distribuidas se pueden obtener a partir de las TABLAS DE MOMENTO DE EMPOTRAMIENTO PERFECTO que puedes verificar en el enlace.

El único factor a tomar en cuenta es que las tablas de momento de empotramiento perfecto del enlace (y de cualquier bibliografía clásica en general) muestra la reacción de los empotramientos ante la carga en particular. Sin embargo nosotros no queremos la reacción en el apoyo sino la carga equivalente en los nudos producto de la carga distribuida aplicada, por tanto debemos invertir los dignos de las REACCIONES de los apoyos para volverlas ACCIONES de la carga en los nudos.

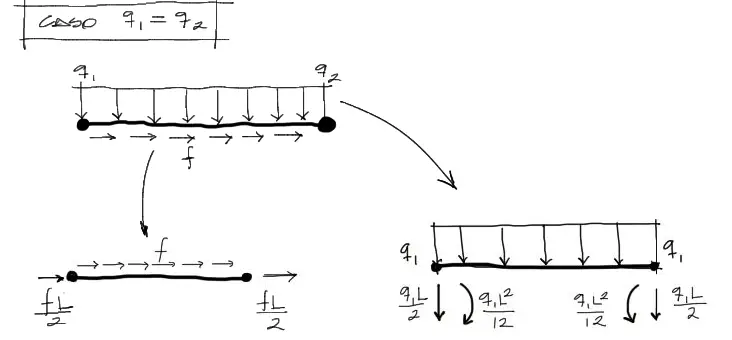
Caso de elemento con carga longitudinal y q1=q2

Este es el caso particular más sencillo, pues se trabaja simplemente con la carga q1 y con la carga longitudinal f. El resultado es como sigue:

Caso de elemento con carga longitudinal y q1>q2

La carga longitudinal se mantiene igual que en los casos anteriores. La carga trapezoidal sin embargo debe cargarse esta vez separando la carga triangular bajo la resta (q1-q2). Luego se convierte estas cargas a cargas puntuales equivalentes.

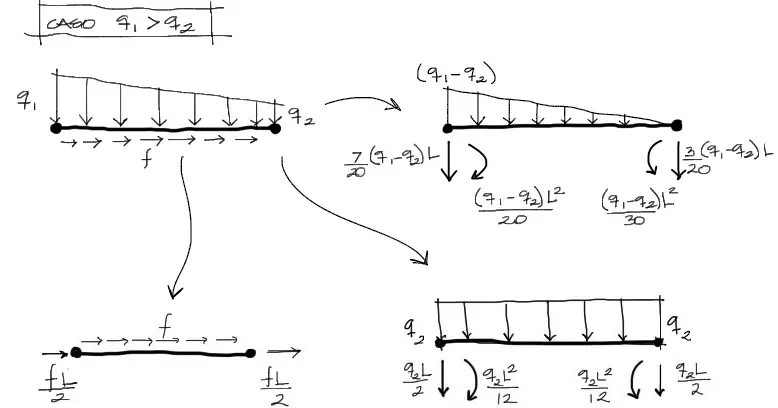
Cabe notar que esta distinción de tres casos se realiza para una programación más limpia de los casos de carga.

Caso de carga curva o de forma arbitraria

Cuando nos topemos con una carga arbitraria curva o de formas que no se acomoden a las mencionadas hasta ahora, se deberá discretizar el elemento de barra en tramos de tal manera que la carga curva pueda ajustarse por lo menos parcialmente a la carga curva original. Mientras más divisiones impongamos en el tramo, más precisos serán los resultados deseados, sin embargo en general con 4 divisiones como las mostradas en el gráfico, puede ser suficiente para la mayoría de los casos de análisis.

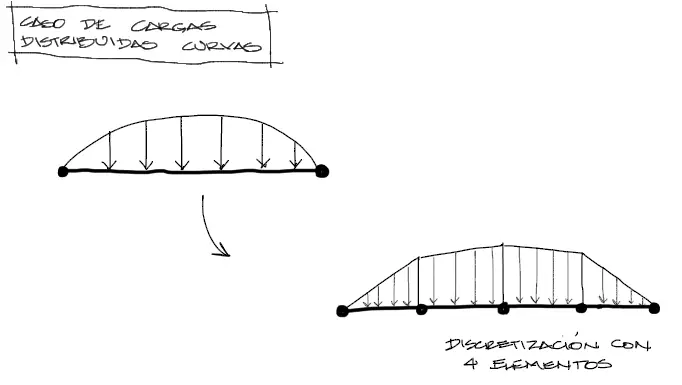
Los conocidos del tema de elementos finitos se darán cuenta de que no es necesario dividir la barra en 4 elementos y más bien pueden utilizarse barras con más de dos nudos y con funciones de interpolación de orden mayor a 4. Sin embargo esa explicación no está dentro de los alcances de este artículo.

Vector de fuerzas equivalentes elementales

Una vez que tenemos calculadas las fuerzas equivalentes en los nudos, debemos acomodar estas fuerzas en un vector de cargas elementales para un ELEMENTO HORIZONTAL de dos nudos, como se muestra a continuación. En esta figura usamos de elemplo el caso de q1<q2.

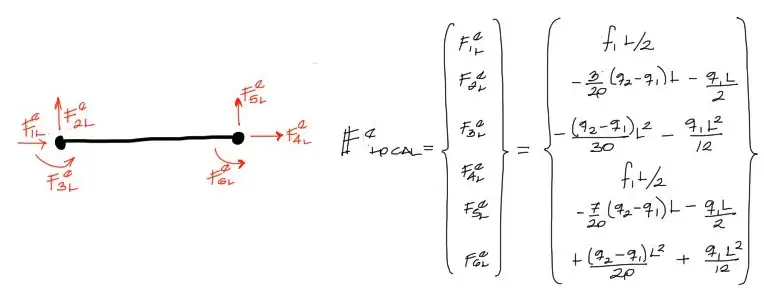
Debemos notar que el elemento inicialmente siempre será horizontal, y que posteriormente deberemos realizar la rotación del elemento en el ángulo final con el que se acoplará al resto de la estructura. En este sentido, si queremos cargar una barra tipo «Columna» con la carga uniforme paralela al eje longitudinal denotada por «f» en los anteriores subtítulos, debemos cargarla como carga horizontal apuntando en la dirección negativa (izquierda) y luego rotar el elemento 90°. Sin embargo de la rotación hablaremos a continuación.

Rotación del vector de fuerzas equivalentes

Habíamos indicado que el vector elemental de fuerzas equivalentes es inicialmente horizontal. Para rotar el vector elemental de fuerzas equivalentes se debe multiplicar a este vector por una matriz de transformación ya utilizada en el artículo de obtención de la matriz de rigidez elemental para el elemento de pórtico. Está matriz denotada por la letra [T] se transpone y multiplica por delante al vector de fuerzas equivalentes Como se muestra en la imagen siguiente.

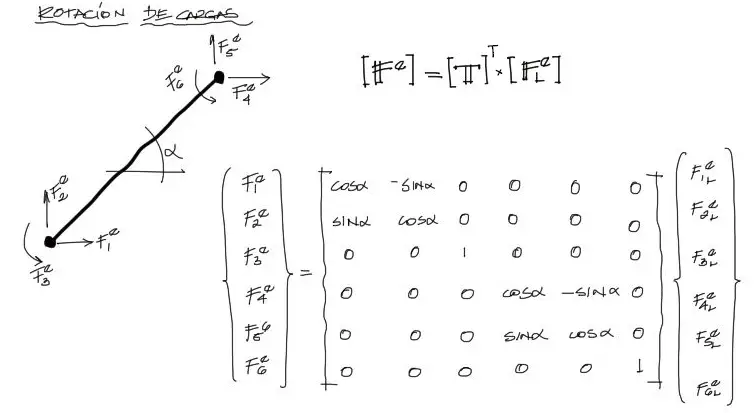
Se deberá recalcar que el ángulo medido para la rotación del elemento parte siempre desde el eje x positivo y por convención el giro será antihorario positivo.

En general para elementos de viga el ángulo de rotación será 0 y para columnas será de 90 grados.

Ensamblaje del vector de fuerzas equivalentes de toda la estructura

Para el ensamblaje del vector de fuerzas equivalentes global o de toda la estructura a partir de los vectores de fuerza elementales se deben seguir los mismos lineamientos que para el ensamblaje de la matriz de rigidez global.

Se deberá primeramente generar un vector lleno de ceros con un número de filas igual al número de grados de libertad de toda la estructura. Posteriormente este vector se irá llenando a partir de los vectores de fuerza elementales rotados de cada elemento.

Se tomará como ejemplo un pórtico como el de la figura siguiente, con los elementos numerados con etiquetas azules, y con los grados de libertad numerados con rojo.

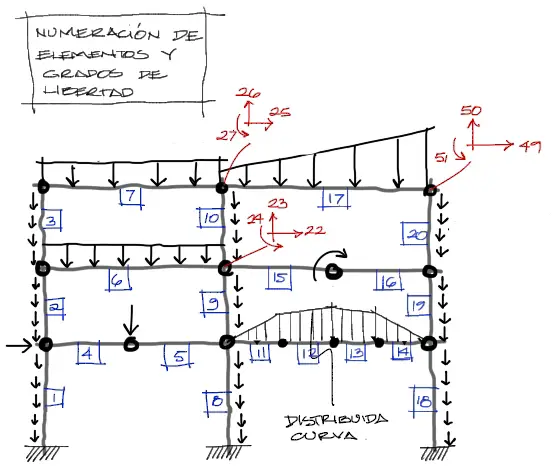
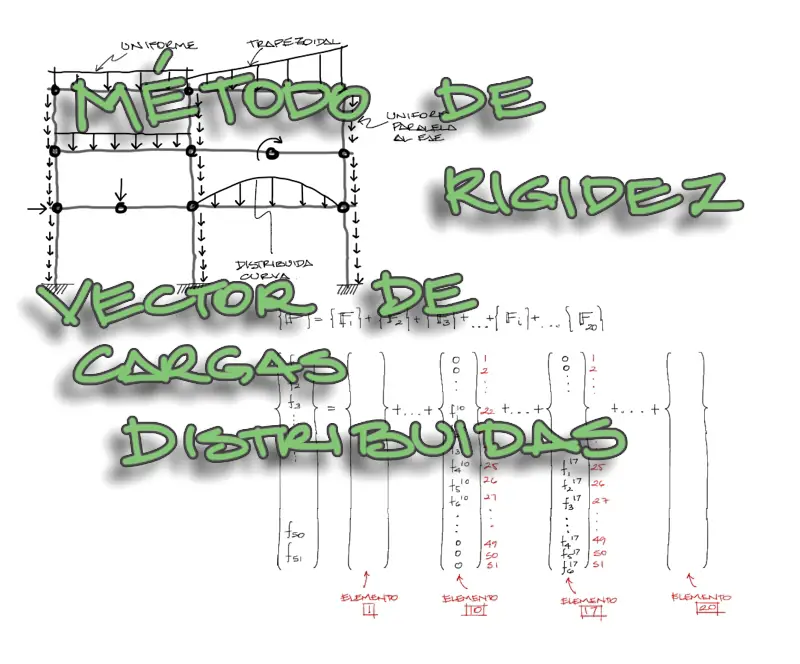
Por ejemplo el elemento 10 ya rotado 90° tomará con sus 6 elementos las posiciones 22, 23, 24, 25, 26, 27 dentro del vector de fuerzas equivalentes global. Una cosa similar sucede con el elemento 17 que toma posiciones 25, 26, 27 y luego saltar hasta las posiciones 49, 50, 51 dentro del vector de fuerzas global. Esto se ve en la siguiente imagen.

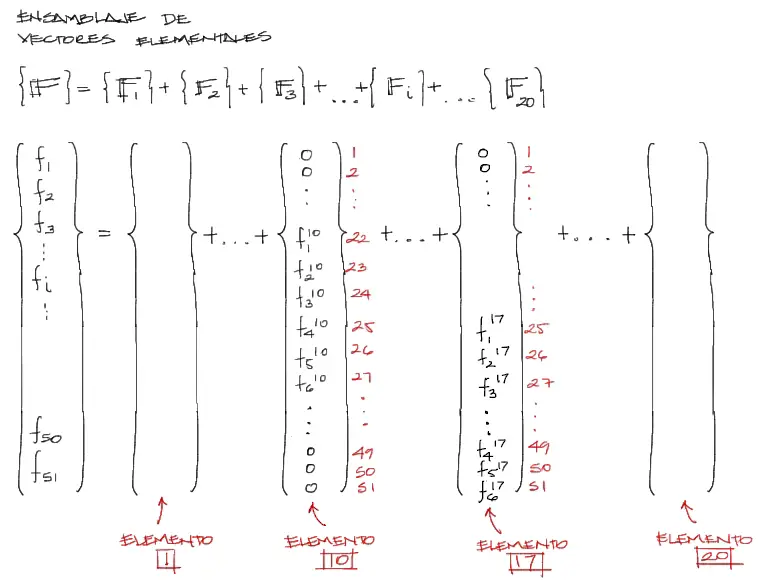
De manera esquemática se muestran los vectores de cada elemento ya con las posiciones globales para sus 6 fuerzas equivalentes por elemento. Finalizado este paso las cargas equivalentes de toda la estructura [F] deberán sumarse al vector de cargas puntuales [Q] encontrado en la anterior publicación.

¿Qué sigue?

Cuando ya se tiene el sistema de ecuaciones completo se debe resolver el sistema reduciendolo a partir de los desplazamientos conocidos. Esto se verá en un siguiente artículo.

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS ←←←