Enunciado
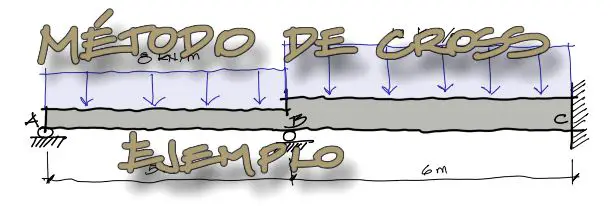
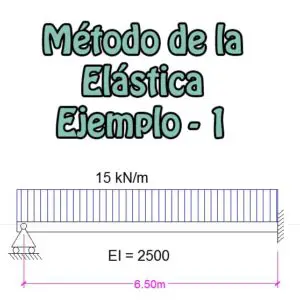
Se pide resolver la siguiente viga por el método de Cross o de distribución de momentos
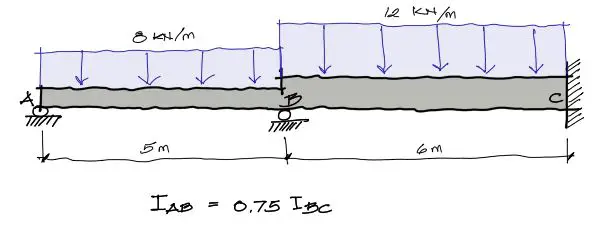
Como se ve en el enunciado, la viga es de sección variable, donde no se indican explícitamente las secciones sino se da una relación de inercias entre tramos.
Resolución
Factores de rigidez relativa
Como se mencionó anteiormente, no se tienen las secciones de la viga, pero para propósitos de cálculo de solicitaciones, es suficiente con conocer la relación relativa de inercias entre tramos. Si se quisieran conocer las deflexiones de la viga, recién serían necesarias las inercias y además módulo elástico de cada tramo.

Los factores de rigidez relativa para cada tramo son la razón entre la inercia y la longitud de ese tramo. Se utiliza la inercia del tramo Ibc como referencia para el análisis y se asume Ibc=1 para tener factores numéricos (recuerda que no es importante la inercia sino la relación de inercias entre tramos).
Factores de distribución
Se calculan a partir de “K” del anterior inciso, los factores de distribución. En el caso de vigas obedecen a la razón entre el factor del tramo, dividido entre la suma de factores concurrentes en el nudo de análisis.
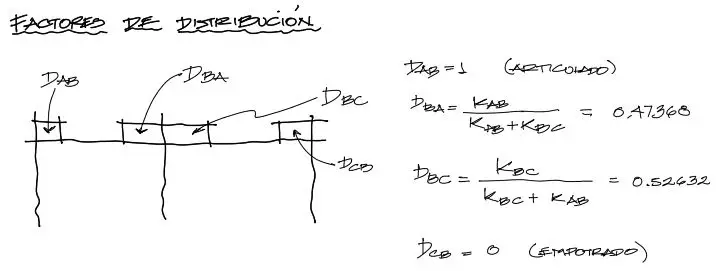
Cuando se calcula el factor de distribución en un apoyo articulado de extremo, este D es igual a 1. Cuando el factor de distribución cae en empotramiento, éste vale cero.
Momentos de empotramiento perfecto
Estos MEP (momentos de empotramiento perfecto) pueden obtenerse a partir de tablas que tengo publicadas en TABLAS DE MOMENTO DE EMPOTRAMIENTO PERFECTO.
Para el caso de los dos tramos de análisis, la carga es uniformemente distribuida, por tanto:
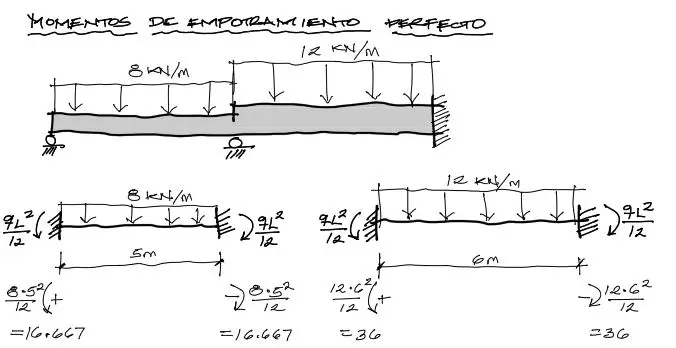
El sentido de las reacciones de momento flector es importante. Se toma antihorario positivo como convención de signos.
Creación de tabla de Cross
Se comienza dibujando la tabla con sus dos tramos, los factores de distribución en las casillas correspondientes y los momentos de empotramiento perfecto debajo de la línea horizontal. Nota que los signos son importantes.
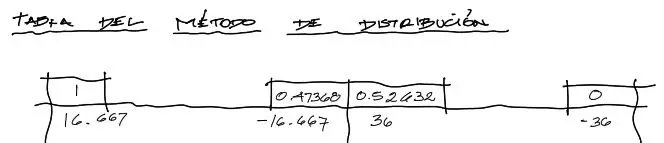
Iteraciones
Se comienza con las iteraciones. Se puede comenzar equilibrando cualquier nudo. Por sistematizar el proceso, equilibraremos los nudos de izquierda a derecha. Comenzando con el nudo izquierdo, el desequilibrio de 16.667 se debe compensar con un momento igual y de signo opuesto pues el momento en el apoyo izquierdo por concepto debe ser cero (apoyo articulado de extremo). Por tanto se tiene:

Una vez equilibrado el nudo a cero, se debe dibujar una línea debajo del momento de equilibrio, indicando que el nudo está equilibrado.
Luego se pasa la mitad del momento de equilibrio al frente de la casilla, como se muestra en la figura. Se conserva el signo.

Posteriormente se equilibra el nudo central. Este suele ser un paso confuso. Se procede como en las burbujas rojas mostradas en la imagen siguiente.
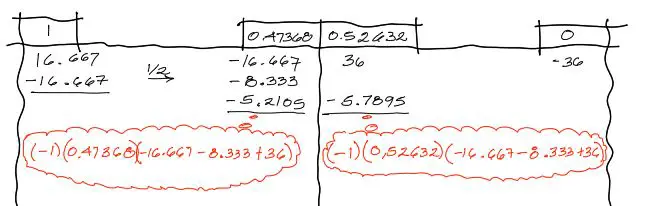
Se suman todos los momentos de desequilibrio, incluyendo el 1/2 momento que llegó del extremo izquierdo. Se deben sumar los momentos conservando sus signos. Se multiplica la suma a cada lado por su correspondiente factor de distribución y el resultado se anota debajo con el signo cambiado. Equilibrados ambos lados, se dibujan líneas horizontales indicando que el nudo ha sido equilibrado
Si analizas y sumas las dos columnas centrales verticalmente, notarás que la suma de ambas columnas ahora es igual. Esto no sucedía antes del equilibrio.
Posteriormente se pasan las mitades de los momentos de equilibrio a sus respectivos frentes conservando el signo como se muestra en la imagen siguiente:

Se procede con el equilibrio del nudo derecho, sin embargo como su factor de distribución es igual a cero, el nudo solo recibe momentos y estos no necesitan compensarse. O sea, -2.8947(0) = 0. No hay momento de compensación. Se podría en términos coloquiales decir que el empotramiento solo recibe momentos.
En la siguiente iteración pasamos nuevamente al nudo izquierdo. Solo se equilibran los momentos que están por debajo de la línea horizontal, como se muestra en la imagen siguiente:

Nuevamente, equilibrado el nudo a cero, se pasa la mitad al frente conservando el signo:

De nuevo, se equilibran solo los momentos por debajo de la línea horizontal. En este caso existe un solo momento desequilibrado de 1.3026, por tanto solo este valor de desequilibrio se multiplica por los factores de distribución y se cambia de signo, como se muestra a continuación en las burbujas rojas:
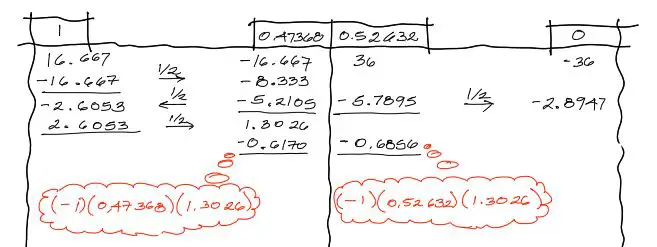
Se pasan las mitades a sus respectivos frentes conservando el signo:

Y se procede de la misma manera hasta buscar una precisión lo suficientemente buena como para que los momentos sean representativos.

La precisión buscada está en función a la cantidad de cifras significativas a tomar en cuenta. Por ejemplo si quiero 5 cifras significativas de precisión, debo buscar en este ejemplo, que los momentos de desequilibrio esten por debajo del milésimo (que existan dos ceros después del punto decimal). Ahí se llegó a una precisión suficientemente buena.
El paso final dentro de la tabla del método consiste en sumar todas las columnas verticalmente. En los nudos o apoyos centrales de vigas, el momento flector siempre debe ser igual y de signo opuesto en las dos columnas.
Postproceso. Análisis de datos
Si dibujamos los resultados obtenidos en la tabla anterior dentro de los dos tramos de viga separados imaginariamente, obtenemos el siguiente esquema:

Respetando siempre la dirección del giro antihoriario positivo, podemos ver que en el apoyo central los momentos traccionan las fibras superiores y comprimen las fibras inferiores. Esto concuerda con el comportamiento de una viga tradicional con carga vertical hacia abajo.
Algo que también debes notar es que esta interpretación de los signos de los momentos flectores es diferente a la interpretación del signo del momento dentro de los diagramas de momento flector. Dentro de los diagramas, un momento negativo indica tracción de las fibras superiores y un momento positivo indica tracción de las fibras inferiores, como se verá a continuación.
Cortantes
Para obtener las solicitaciones de cortante en cada tramo, basta equilibrar cada tramo como si fuera un diagrama de cuerpo libre, donde los cortantes son las incógnitas. Se dibujan las cortantes con la convención de signos positiva según el diagrama de cortantes.
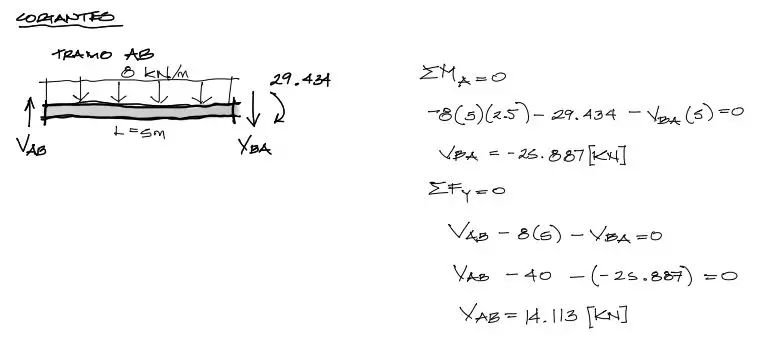
Posteriormente se realiza el equilibrio vertical. Como existen dos incógnitas Vab y Vba, se necesitan dos ecuaciones: Suma de fuerzas verticales igualadas a cero y suma de momentos de fuerza igualados a cero. Se toma como pivote de la suma de momentos el extremo izquierdo de la barra.
Para el segundo tramo el procedimiento es exáctamente el mismo
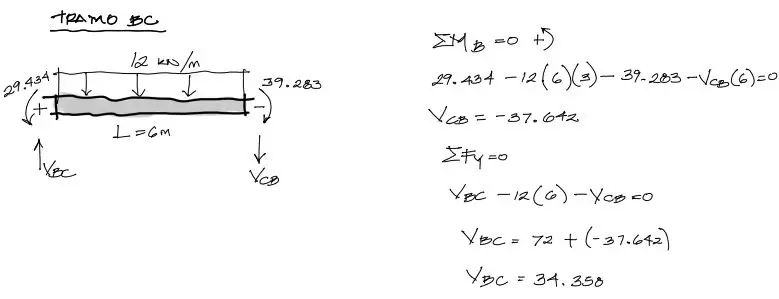
Finalmente obtenidos los cuatro cortantes incógnita de los extremos, graficamos el cortante. Por definición sabemos que el cortante es una línea recta si la carga es horizontal y constante. Además la recta del diagrama de cortante para cada tramo tiene una pendiente igual a la magnitud de la carga.
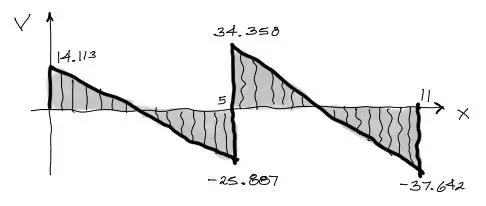
Diagrama de momento flector
Encontrado el diagrama de cortante, debemos trabajar un poco más con ciertos datos que no se muestran explícitamente en el gráfico del anterior subtítulo.
Se sabe por definición que los diagramas de momento flector son la integral de los diagramas de cortante, por tanto si acumulamos áreas del diagrama de cortante podemos dibujar fácilmente el diagrama de momentos flectores.
Para conocer las áreas de los triángulos del diagrama de cortante necesitamos saber los lugares donde el diagrama de cortante intersecta con el eje de las X. Para eso, para el primer triángulo, se puede dividir el cortante entre la carga. O sea 14.113/8 = 1.764m. El mismo procedimiento se realiza para los otros tres triángulos.
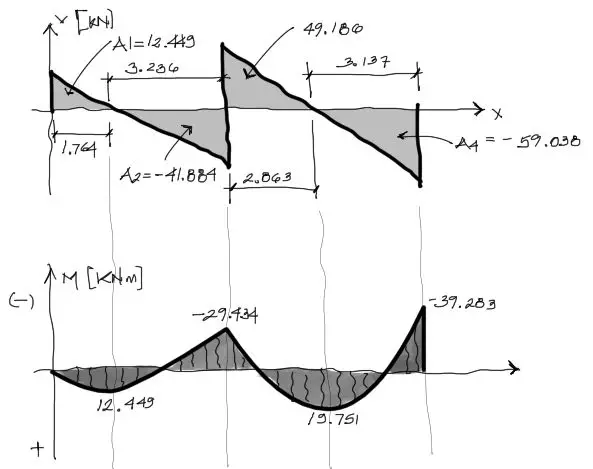
A partir de las áreas encontradas de los triángulos, comenzando de momento cero a la izquierda de la viga (porque el apoyo articulado siempre genera momento nulo en extremo) se van acumulando las áreas de izquierda a derecha del diagrama generando parábolas. Se supone que la integral de una recta con pendiente es una parábola y eso es precisamente lo que muestra un diagrama de momentos flectores como el que se muestra en la imagen arriba.
autor: Marcelo Pardo

Hola
Puede esplicar nuevamente lo de las rigideces de cada tramo por favor, ya que no me queda claro, gracias