Planteamiento
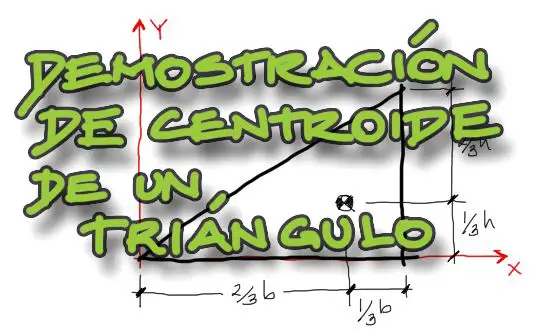
El problema es clásico: Encontrar el centroide de un triángulo rectángulo genérico como el de la figura:
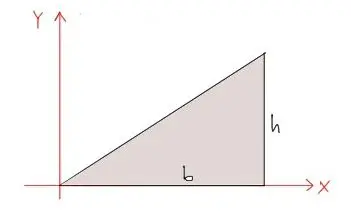
Solución
Centroide X
Después del rectángulo, este es uno de los problemas más fáciles de resolver en cuanto a centroides de figuras geométrias. Se debe conceptualizar un diferencial de área mapeando entre los límites 0 y b para «x» y entre 0 y la ecuación de la recta para «y». En este caso la ecuación de la recta es y=h·x/b, como en la figura:
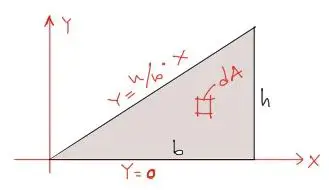
Luego para el centroide en x, aplicamos la fórmula de centroides en base a integrales teniendo:
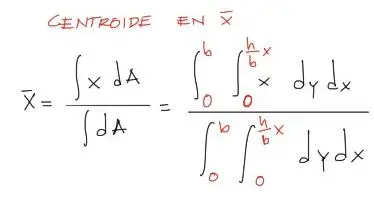
Resolviendo la integral, se tiene el siguiente procedimiento. Ten en cuenta que cuando la integral está en función de «y», la variable «x» trabaja como constante.
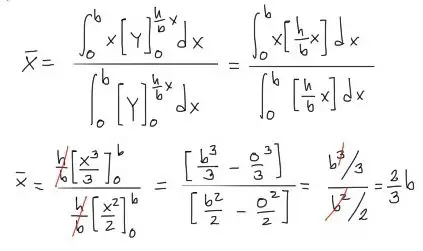
Entonces el centroide en «x» del triángulo está a 2/3 del extremo izquierdo, como seguramente ya sabías.
Centroide Y
Para el centroide en Y se aplica la fórmula correspondiente a centroides respecto a este eje. El procedimiento es muy parecido. Solo se debe tener en cuenta que en la integral del numerador, la integral de y·dy ahora debe integrarse quedando y²/2 y luego reemplazar los respectivos límites.
Centroide X (solución alternativa)
Muchas veces se prefiere no utilizar doble integración, sino solo una integral simple. Para eso el diferencial de área debe definirse como una franja vertical de ancho «dx» y de altura igual a la altura del triángulo:
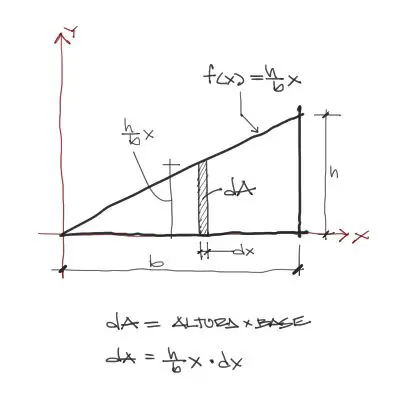Luego esto puede integrarse a lo largo de x, desde cero hasta b, quedando la misma integral de arriba.
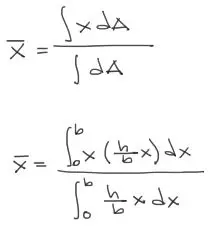
Concluyendo
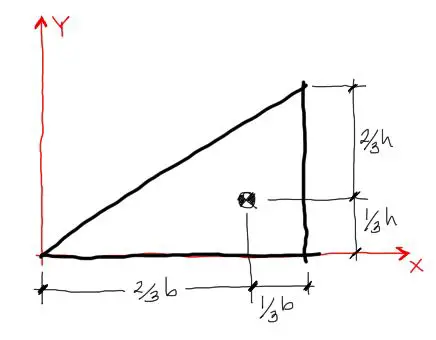
Con esto termina la demostración. Concluyendo, el centroide en X y Y de un triángulo está a 1/3 de la base y de la altura medidos ambos a partir del vértice recto del triángulo.
autor: Marcelo Pardo
