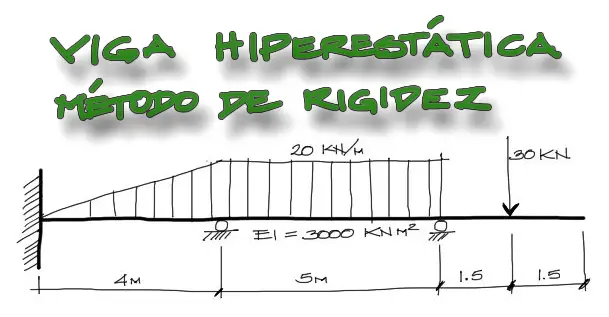
Enunciado

Dada la viga mostrada, se deben encontrar los desplazamientos producto de las cargas aplicadas a la viga.

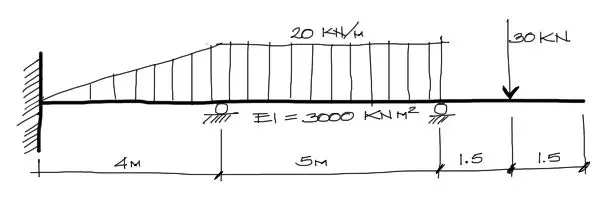
Solución

La solución en vídeo del problema puedes verla en:

La solución en texto en forma detallada está a continuación

Paso 1 – Enumeración de nudos y elementos

Antes de enumerar los nudos y los elementos, se debe tener presente donde colocar los nudos. Estos deben colocarse en todos los puntos donde exista:

• un apoyo
• un cambio en el tipo de carga
• una carga puntual
• un momento de fuerza
• un desplazamiento inducido

Luego, enumeramos cada grado de libertad, cada nudo y cada elemento.

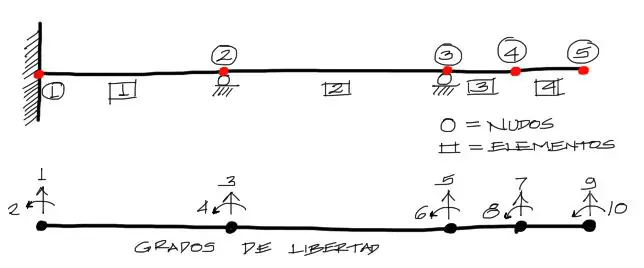
Nota que al momento de asignar los grados ed libertad a los nudos, solo se asigan dos por nudo. Uno correspondiente a los desplazamientos verticales y otro para los giros.

en este caso no se necesitan desplazamientos horizontales pues los elementos de viga, a diferencia de los pórticos, podemos asumir que no se deforman axialmente

Paso 2 – Se arman las matrices de rigidez de cada elemento

El método matricial consiste en el desgloce de la viga en pequeñas partes. Cada una de estas partes o tramos de la viga contiene propiedades que matemáticamente y en notación matricial pueden escribirse según:

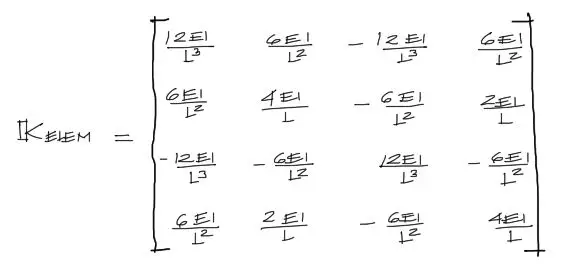
Esta es llamada Matriz de Rigidez de un elemento. Esta matriz de rigidez relaciona las fuerzas y momentos aplicadas en los nudos con los desplazamientos y giros de estos mismos nudos mediante la ecuación:

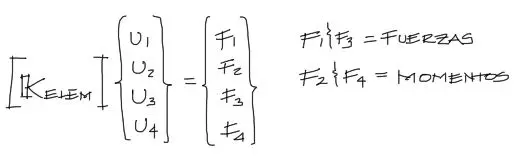
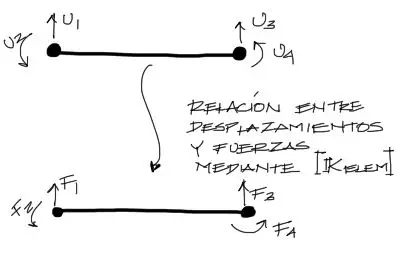
Gráficamente, sucede lo siguiente:

Entonces, con los datos correspondientes a cada tramo de viga (cada elemento), se deben encontrar las matrices de rigidez correspondientes. Existen 4 tramos, por tanto 4 elementos, y 4 matrices de rigidez elementales:

Por ejemplo, el elemento 1 tiene una longitud L = 4m; EI = rigidez = 3000 KNm². Se reemplazan estos datos en la matriz 4×4 de arriba, resultando:

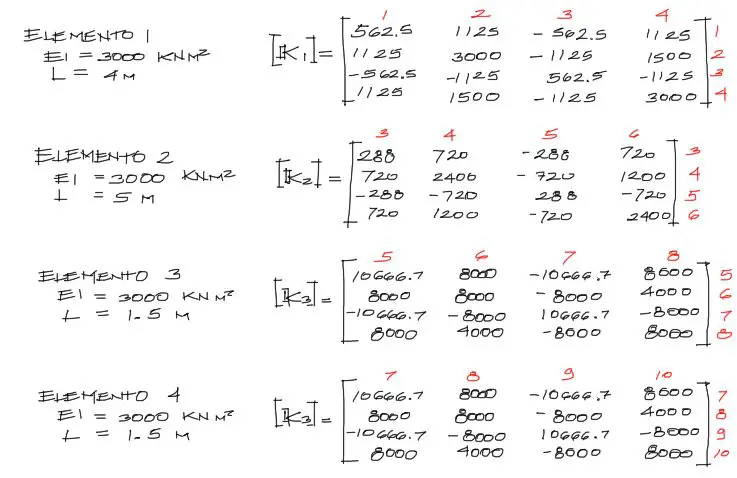
Nota: Cuando generes una matriz de rigidez elemental, es buena práctica anotar los grados de libertad a los que corresponde esta matriz elemental. Esto te ayudará a ensamblar la matriz de rigidez global más adelante. Por ejemplo, la segunda matriz de rigidez va del nudo 2 al 3. Los grados de libertad del nudo 2 y 3 respectivamente son 3,4,5,6 y estos grados de libertad deberás anotarlos ordenadamente sobre y al lado de la matriz de rigidez elemental, como ves en números vertes en la imagen arriba.

Te dejo nuevamente la imagen de grados de libertad acá abajo:

Paso 3 – Ensamblaje de la Matriz de rigidez

Para este paso, imagina que existe una matriz vacía de dimensión 10×10 (la misma cantidad de grados de libertad que existen en toda la viga) donde iremos colocando las matrices elementales una a una, según la posición que le corresponda.

Por ejemplo, trasladamos la matriz de rigidez del elemento 1 (de color azul) hacia la matriz vacía de 10×10.

Luego trasladamos la matriz elemental del segundo elemento (pintada de magenta). Notarás que los grados de libertad que le corresponden en la matriz global son 3,4,5,6 y se superponen con la primera matriz. En caso de tener matrices de rigidez elementales superpuestas, sus elementos se suman.

Se repite el procedimiento para los otros dos elementos

La ecuación generada [K global]{U global}={F global} con todos los elementos sumados es:

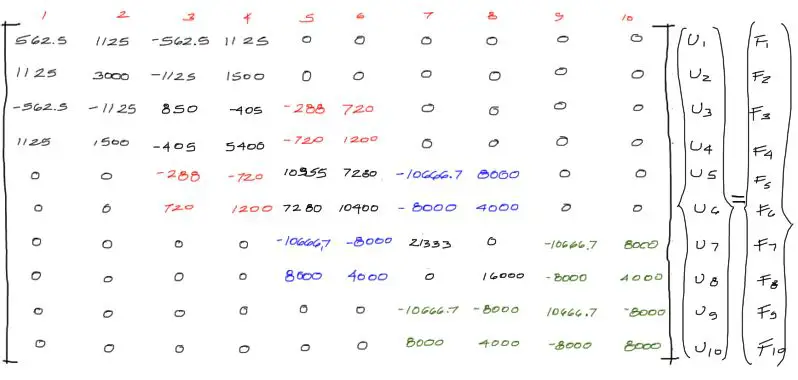
Esta ecuación aun no puede resolverse pues es singular (infinitas soluciones). Se encontrará una única solución al problema en el momento en que se apliquen las condiciones del contorno del problema. En eso consiste el siguiente paso.

Paso 4 – imposición de condiciones de contorno y cargas

Vamos a volver a dibujar la viga con sus condiciones de contorno:

De esta figura, los grados de libertad restringidos son los respectivos a los apoyos que impiden que la viga gire o se desplace en ese sector. Por ejemplo el empotramiento impide que los grados de libertad 1, 2 se desplacen o giren, por tanto U1 y U2 son cero.

Lo mismo sucede con los grados de libertad 3 y 5. No pueden desplazarse verticalmente por tanto son cero.

Luego, donde los desplazamientos son cero, las reacciones son desconocidas o incógnitas.

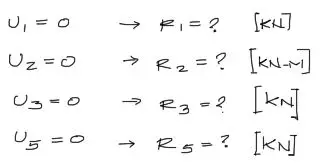
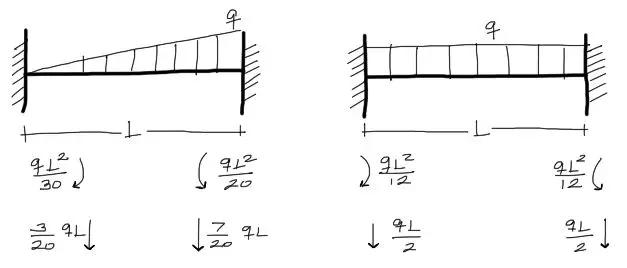
Para cargar la viga, se deben transformar las cargas distribuidas en cargas equivalentes puntuales en los extremos del tramo.

Estas cargas equivalentes salen de los Momentos de empotramiento perfecto. Se pueden deducir o pueden consultarse en bibliografía.

Para cargas triangulares y uniformes, las cargas y momentos equivalentes en los extremos son los siguientes:

Entonces, cada una de estas cargas equivalentes debe cargarse en el vector de fuerzas y momentos en el sistema de ecuaciones lineal en el grado de libertad correspondiente.

Las cargas puntuales como la carga de 30 KN no necesita transformarse a carga equivamente pues esta ya es una carga aplicada directamente sobre un nudo.

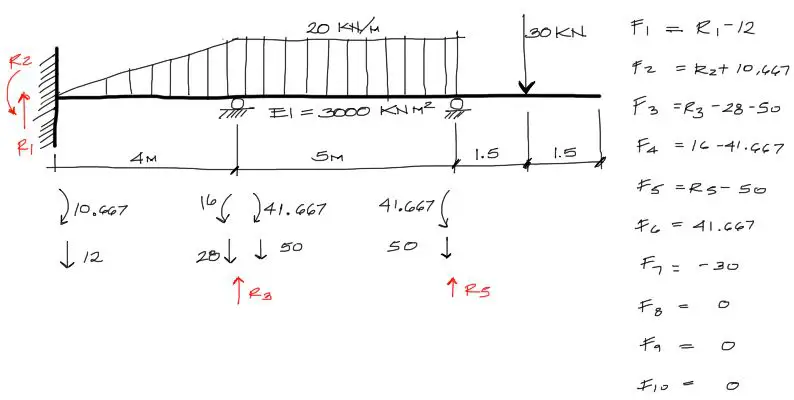
Así, por ejemplo para el grado de libertad 3, las cargas que concurren en este grado de libertad son:

• La carga equivalente de 28 KN producto de la carga triangular
• La carga equivalente de 50 KN producto de la carga distribuida
• La reacción R3 producto del apoyo.

Estas tres fuerzas se anotan en el vector de fuerza en el grado de libertad 3.

Lo mismo se repite tanto para momentos como para fuerzas en los grados de libertad que correspondan, quedando por tanto:

Terminado este paso, el sistema de ecuaciones [K]{u}={F} queda como en la siguiente imagen:

Resolución del sistema de ecuaciones

Para resolver el sistema, se debe previamente eliminar del sistema, las filas y columnas correspondientes a los grados de libertad restringidos. En este caso filas y columnas 1, 2, 3 ,5.

De esta manera nos quedan como incógnitas sólamente los desplazamientos desconocidos:

Esta eliminación de filas y columnas podría parecer arbitraria, sin embargo no la es. Se eliminan las columnas 1, 2, 3, 5 ya que al multiplicar [K] por {u}, los coeficientes que acompañan a los desplazamientos iguales a cero, obviamente se eliminan en la multiplicación.

El sistema de ecuaciones reducido mostrado ahora se resuelve de la manera clásica, mediante inversión de la matriz de rigidez reducida, o mediante metodos como Gauss-jordan o cualquier método similar.

Aplicando las fórmulas mostradas a nuestro ejercicio se tiene entonces:

Cuyo resultado será el siguiente:

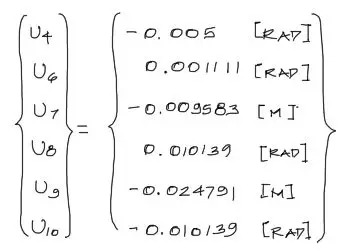
Los desplazamientos encontrados están en unidades de [m] para los U’s impares y en radianes para los U’s pares

Reacciones

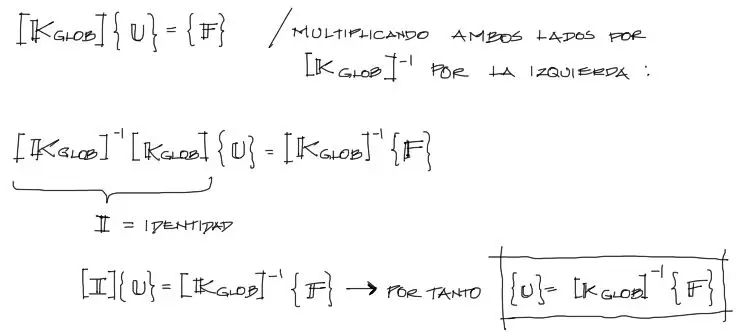
Si se quieren encontrar las reacciones R1, R2, R3, R5 solo se deben reemplazar los desplazamientos encontrados justo arriba y reemplazarlos en el sistema de ecuaciones global de 10×10. De esa manera se tiene:

Multiplicando los dos miembros de la izquierda, se obtiene un vector de 10×1 que se iguala con el vector 10×1 de la derecha:

Cada término de la izquierda se iguala con cada término de la derecha. En las filas donde existen las incógnitas se despejan las respectivas reacciones. En las filas donde no existan incógnitas simplemente se verifica la identidad.

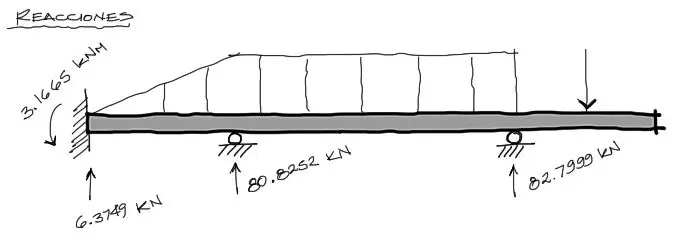
Y con esto finaliza la solución de las reacciones de la viga. Reescribiendo las reacciones en la viga se tiene:

¿Qué sigue?

En el LINK DEL VÍDEO se explicará como encontrar las ecuaciones de Momento y de Cortante a partir de los desplazamientos y giros en los nudos de la viga.

También tienes la explicación en texto para comprobar paso a paso los resultados del método. La publicación escrita la encuentras en ESTE LINK

autor: Marcelo Pardo

← ← ← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS← ← ←